POJ 2149 & ZOJ 2267&UVA 1337&UVALive 3192 Inherit the Spheres

题目链接：http://poj.org/problem?id=2149

题意：给出一些球。现在要将一个平行于XOY的平面从最底端移到最上端，移动过程中，平面会切割这些球，切割时球的切面会在平面上留下痕迹，而随着平面的上移，平面上的痕迹的联通块数会不断变化。现在要求出联通块数的变化情况：1、输出变化的次数；2、对于每一次如果块数增加就输出1，否则输出0。如下图，变化为012123210，输出11011000。

 

 

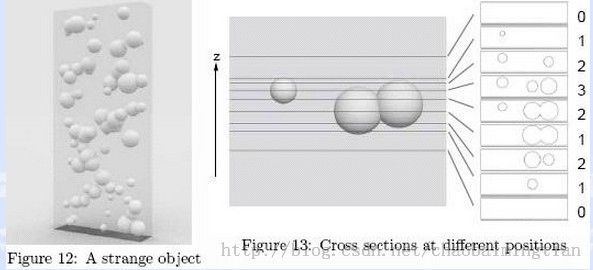
思路：总的思路分为两步，第一步求出所有沿z向上的分界点；第二步，枚举分界点，求连通块数。

（1）第一步主要问题是求两个球相交区域的最上最下的z坐标。首先，将两个球中的一个a平移到原点（设这个平移向量为A），另一个b作相同向量的平移，此时ab均还是在一个三维坐标下。下面，我们将其变换到二维坐标下，令a=(0,0),设b之前的坐标为(x,y,z)，现在令b=(sqrt(x*x+y*y),z)，那么ab就转换到了二维坐标下。此时，ab交点的纵坐标就是z（从b的转换可以看出z是不变的），然后z+A.z就是原来的球的交点z坐标。另外，在计算二维坐标下两个圆的交点时，可以将b再通过旋转变换到x轴上，这些就是二维的问题了，不再细说了；
（2）将所有分界点排序之后，每次枚举两个相邻分界点的中点，求联通块数。

 

 

int sgn(double x)
{
    if(x>EPS) return 1;
    if(x<-EPS) return -1;
    return 0;
}


struct point
{
    double x,y;
    
        
    point(){}
    point(double _x,double _y)
    {
        x=_x;
        y=_y;
    }
    
    void get()
    {
        RD(x); RD(y);
    }
    
    point operator+(point a)
    {
        return point(x+a.x,y+a.y);
    }
    
    point operator-(point a)
    {
        return point(x-a.x,y-a.y);
    }
    
    double operator*(point a)
    {
        return x*a.y-y*a.x;
    }
    
    point operator*(double t)
    {
        return point(x*t,y*t);
    }
    
    double operator^(point a)
    {
        return x*a.x+y*a.y;
    }
    
    double len()
    {
        return sqrt(x*x+y*y);
    }
    
    point zhuanShun(double t)
    {
        return point(x*cos(t)+y*sin(t),y*cos(t)-x*sin(t));
    }
    
    point zhuanNi(double t)
    {
        return point(x*cos(t)-y*sin(t),x*sin(t)+y*cos(t));
    }
    
    point adjust(double L)
    {
        double d=len();
        L/=d;
        return point(x*L,y*L);
    }
    
    void print()
    {
        printf("%.3lf %.3lf\n",x+EPS,y+EPS);
    }
};


double len(point a)
{
    return a.len();
}


struct point3
{
    double x,y,z;
    
    point3(){}
    point3(double _x,double _y,double _z)
    {
        x=_x;
        y=_y;
        z=_z;
    }
    
    void get()
    {
        cin>>x>>y>>z;
    }
    
    point3 operator+(point3 a)
    {
        return point3(x+a.x,y+a.y,z+a.z);
    }
    
    point3 operator-(point3 a)
    {
        return point3(x-a.x,y-a.y,z-a.z);
    }
    
    point3 operator*(point3 a)
    {
        return point3(y*a.z-z*a.y,z*a.x-x*a.z,x*a.y-y*a.x);
    }
    
    point3 operator*(double t)
    {
        return point3(x*t,y*t,z*t);
    }
    
    double operator^(point3 a)
    {
        return x*a.x+y*a.y+z*a.z;
    }
    
    point3 operator/(double t)
    {
        return point3(x/t,y/t,z/t);
    }
    
    double len()
    {
        return sqrt(x*x+y*y+z*z);
    }
    
    point3 adjust(double L)
    {
        double t=len();
        L/=t;
        return point3(x*L,y*L,z*L);
    }
    
    void print()
    {
        printf("%.10lf %.10lf %.10lf\n",x+EPS,y+EPS,z+EPS);
    }
};




double len(point3 a)
{
    return a.len();
}




double getArea(point3 a,point3 b,point3 c)
{
    double x=len((b-a)*(c-a));
    return x/2;
}
    
double getVolume(point3 a,point3 b,point3 c,point3 d)
{
    double x=(b-a)*(c-a)^(d-a);
    return x/6;
}


point3 pShadowOnPlane(point3 p,point3 a,point3 b,point3 c)
{
    point3 v=(b-a)*(c-a);
    if(sgn(v^(a-p))<0) v=v*-1;
    v=v.adjust(1);
    double d=fabs(v^(a-p));
    return p+v*d;
}


double lineToLine(point3 a,point3 b,point3 p,point3 q)
{
    point3 v=(b-a)*(q-p);
    return fabs((a-p)^v)/len(v);
}


int pInPlane(point3 p,point3 a,point3 b,point3 c)
{
    double S=getArea(a,b,c);
    double S1=getArea(a,b,p);
    double S2=getArea(a,c,p);
    double S3=getArea(b,c,p);
    return sgn(S-S1-S2-S3)==0;
}


int opposite(point3 p,point3 q,point3 a,point3 b,point3 c)
{
    point3 v=(b-a)*(c-a);
    double x=v^(p-a);
    double y=v^(q-a);
    return sgn(x*y)<0;
}


int segCrossTri(point3 p,point3 q,point3 a,point3 b,point3 c)
{
    return opposite(p,q,a,b,c)&&
            opposite(a,b,p,q,c)&&
            opposite(a,c,p,q,b)&&
            opposite(b,c,p,q,a);
}


double pToPlane(point3 p,point3 a,point3 b,point3 c)
{
    double v=((b-a)*(c-a)^(p-a))/6;
    double s=len((b-a)*(c-a))/2;
    return fabs(3*v/s);
}




double pToLine(point3 p,point3 a,point3 b)
{
    double S=len((a-p)*(b-p));
    return S/len(a-b);
}




double pToSeg(point3 p,point3 a,point3 b)
{
    if(sgn((p-a)^(b-a))<=0) return len(a-p);
    if(sgn((p-b)^(a-b))<=0) return len(b-p);
    return pToLine(p,a,b);
}


double pToPlane1(point3 p,point3 a,point3 b,point3 c)
{
    point3 k=pShadowOnPlane(p,a,b,c);
    if(pInPlane(k,a,b,c)) return pToPlane(p,a,b,c);
    double x=pToSeg(p,a,b);
    double y=pToSeg(p,a,c);
    double z=pToSeg(p,b,c);
    return min(x,min(y,z));
}




double getAng(point3 a,point3 b)
{
    double x=(a^b)/len(a)/len(b);
    return acos(x);
}


double segToSeg(point3 a,point3 b,point3 p,point3 q)
{
    point3 v=(b-a)*(q-p);
    
    double A,B,A1,B1;
    A=((b-a)*v)^(p-a);
    B=((b-a)*v)^(q-a);
    
    A1=((p-q)*v)^(a-q);
    B1=((p-q)*v)^(b-q);
    if(sgn(A*B)<=0&&sgn(A1*B1)<=0) 
    {
        return lineToLine(a,b,p,q);
    }


    double x=min(pToSeg(a,p,q),pToSeg(b,p,q));
    double y=min(pToSeg(p,a,b),pToSeg(q,a,b));
    return min(x,y);
}


struct face
{
    int a,b,c,ok;
    
    face(){}
    face(int _a,int _b,int _c,int _ok)
    {
        a=_a;
        b=_b;
        c=_c;
        ok=_ok;
    }
};


struct _3DCH
{
    face F[N<<2];
    int b[N][N],cnt,n;
    point3 p[N];
    
    int getDir(point3 t,face F)
    {
        double x=(p[F.b]-p[F.a])*(p[F.c]-p[F.a])^(t-p[F.a]);
        return sgn(x);
    }
    
    
    void deal(int i,int x,int y)
    {
        int f=b[x][y];
        if(!F[f].ok) return;
        if(getDir(p[i],F[f])==1) DFS(i,f);
        else
        {
            b[y][x]=b[x][i]=b[i][y]=cnt;
            F[cnt++]=face(y,x,i,1);
        }
    }
    
    void DFS(int i,int j)
    {
        F[j].ok=0;
        deal(i,F[j].b,F[j].a);
        deal(i,F[j].c,F[j].b);
        deal(i,F[j].a,F[j].c);
    }
    
    void construct()
    {
        int i,j,k=0;
        for(i=1;i<n;i++) if(sgn(len(p[i]-p[0])))
        {
            swap(p[i],p[1]);
            k++;
            break;
        }
        if(k!=1) return;
        for(i=2;i<n;i++) if(sgn(getArea(p[0],p[1],p[i])))
        {
            swap(p[i],p[2]);
            k++;
            break;
        }
        if(k!=2) return;
        for(i=3;i<n;i++) if(sgn(getVolume(p[0],p[1],p[2],p[i])))
        {
            swap(p[i],p[3]);
            k++;
            break;
        }
        if(k!=3) return;
        
        cnt=0;
        FOR0(i,4)
        {
            face k=face((i+1)%4,(i+2)%4,(i+3)%4,1);
            if(getDir(p[i],k)==1) swap(k.b,k.c);
            b[k.a][k.b]=b[k.b][k.c]=b[k.c][k.a]=cnt;
            F[cnt++]=k;
        }
        
        for(i=4;i<n;i++) FOR0(j,cnt)
        {
            if(F[j].ok&&getDir(p[i],F[j])==1)
            {
                DFS(i,j);
                break;
            }
        }
        j=0;
        FOR0(i,cnt) if(F[i].ok) F[j++]=F[i];
        cnt=j;
    }
    
    point3 getCenter()
    {
        point3 ans=point3(0,0,0),o=point3(0,0,0);
        double s=0,temp;
        int i;
        FOR0(i,cnt)
        {
            face k=F[i];
            temp=getVolume(o,p[k.a],p[k.b],p[k.c]);
            ans=ans+(o+p[k.a]+p[k.b]+p[k.c])/4*temp;
            s+=temp;
        }
        ans=ans/s;
        return ans;
    }
    
    double getMinDis(point3 a)
    {
        double ans=dinf;
        int i;
        FOR0(i,cnt) 
        {
            face k=F[i];
            ans=min(ans,pToPlane(a,p[k.a],p[k.b],p[k.c]));
        }
        return ans;
    }
    
};


/***********************************************************/


point3 a[N];
vector<double> V,V1;
double R[N];
int n;


void deal(point3 a,double ra,point3 b,double rb,int i,int j)
{
    b=b-a;
    point p=point(0,0),q=point(sqrt(b.y*b.y+b.x*b.x),b.z);
    double d=len(b);
    if(sgn(d-ra-rb)==1) return;
    if(sgn(fabs(ra-rb)-d)==1) return;
    
    double ang=atan2(q.y,q.x);
    q=q.zhuanShun(ang);
    double ang1=acos((ra*ra+d*d-rb*rb)/(2*ra*d));
    point v;
    
    v=point(cos(ang1),sin(ang1));
    v=v.adjust(ra); v=v.zhuanNi(ang);
    V.pb(v.y+a.z);
    
    v=point(cos(ang1),sin(-ang1));
    v=v.adjust(ra); v=v.zhuanNi(ang);
    V.pb(v.y+a.z);
}


int visit[N],num;
vector<int> G[N];
point C[N];
double CR[N];


void DFS(int u)
{
    visit[u]=1;
    int i,v;
    FOR0(i,SZ(G[u]))
    {
        v=G[u][i];
        if(!visit[v]) DFS(v);
    }
}


int cal(double z)
{
    vector<int> p;
    int i,j;
    num=0;
    FOR1(i,n) if(sgn(a[i].z-R[i]-z)<=0&&sgn(a[i].z+R[i]-z)>=0)
    {
        p.pb(i);G[i].clear();
        C[num]=point(a[i].x,a[i].y);
        CR[num]=sqr(R[i])-sqr(a[i].z-z);
        if(CR[num]<0) CR[num]=0;
        CR[num]=sqrt(CR[num]);
        num++;
    }
    clr(visit,0);
    double low,high;
    FOR0(i,SZ(p)) for(j=i+1;j<SZ(p);j++)
    {
        if(sgn(len(C[i]-C[j])-CR[i]-CR[j])<=0)
        {
            G[p[i]].pb(p[j]);
            G[p[j]].pb(p[i]);
        }
    }
    int ans=0;
    FOR0(i,SZ(p)) if(!visit[p[i]])
    {
        DFS(p[i]);
        ans++;
    }
    
    return ans;
}






int main()
{
    Rush(n)
    {
        if(!n) break;
        int i,j;
        FOR1(i,n) a[i].get(),RD(R[i]);
        V.clear(); 
        FOR1(i,n) for(j=i+1;j<=n;j++) 
        {
            deal(a[i],R[i],a[j],R[j],i,j);
        }
        FOR1(i,n) V.pb(a[i].z-R[i]),V.pb(a[i].z+R[i]);
        V.pb(-1); V.pb(36001);
        sort(V.begin(),V.end());
        V1.clear();
        
        FOR0(i,SZ(V)) 
        {
            if(i==0||sgn(V[i]-V[i-1])>0) V1.pb(V[i]);
        }
        V=V1;
        vector<int> ans;
        int pre=-1;
        FOR1(i,SZ(V)-1)
        {
            j=cal((V[i]+V[i-1])/2);
            if(j!=pre) ans.pb(j),pre=j;
        }
        PR((int)SZ(ans)-1);
        FOR1(i,SZ(ans)-1) 
        {
            if(ans[i]>ans[i-1]) putchar('1');
            else putchar('0');
        }
        puts("");
    }
}