数学--函数1(初中生都能看懂)
文章目录
- 函数
-
- 函数的概念
-
- 举个例子
- 注意事项
最近有一些空闲的时间了,于是让朋友带来一本高等数学学习一下。
第一章便是 函数,极限和连续 函数,极限和连续 函数,极限和连续。
函数
函数的概念
第一节(1.1.1.1)主要讲了函数的定义,在这里说明一下:
若 X , Y X,Y X,Y 都是是实数集合,则两实数集合之间的映射 f : x → B f:x\xrightarrow{} B f:xB 成为函数。
函数是两个实数集合之间的一种对应法则。
我们说的直白一点,就是对于在函数定义域(就是 x x x 能取到的数)每个数 x x x,都有与这个 x x x 所对应的值 f ( x ) f(x) f(x),也就是初中学的 y y y。这个没什么好说的。
举个例子
我们肯定学过一次函数 f ( x ) = x f(x)=x f(x)=x 这个是一个简单的一次函数。图像也很好画,这里就不过多赘述了。
我们可以使用表格发来列举一下:
| x x x | 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | 5 5 5 | 6 6 6 | 7 7 7 | 8 8 8 | 9 9 9 | 10 10 10 | ⋅ ⋅ ⋅ \cdot\cdot\cdot ⋅⋅⋅ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| f ( x ) f(x) f(x) | 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | 5 5 5 | 6 6 6 | 7 7 7 | 8 8 8 | 9 9 9 | 10 10 10 | ⋅ ⋅ ⋅ \cdot\cdot\cdot ⋅⋅⋅ |
我们发现如果一个数 x ∈ R x\in R x∈R,那么总有一个与之对应的函数值 f ( x ) = x f(x)=x f(x)=x。
注意事项
( 1 ) (1) (1) 函数的概念中包含三个要素- -即为定义域,值域,和对应法则。但是,确定函数的关键是对应法则和定义域。因此对于两个函数来说,当且仅当他们的定义域和对应法则都相同时,这两个函数才是同一个函数。与自变量以及因变量用什么字母表示没有关系。
例如:函数 f ( x ) = x f(x)=x f(x)=x 和函数 f ( x ) = x 2 x f(x)=\displaystyle \frac{x^2}x f(x)=xx2 并不是一个函数,应为在第二个函数 f ( x ) = x 2 x f(x)=\displaystyle \frac{x^2}x f(x)=xx2 中, x x x 的定义与为 x ∈ R x\in R x∈R 并且 x ≠ 0 x\ne0 x=0,但是,在第一个函数中, x x x 的定义域就是 x ∈ R x\in R x∈R。两个函数的定义域明显不同,所以即便两个函数化简过后相同,这两个函数也不一定相同,这就是一个很好的例子。
( 2 ) (2) (2) 关于函数定义域的确定可分为两种情况,对于实际问题,函数的定义域是根据问题的实际意义确定的(例如你去买菜,菜的重量一定不是负数)。对于未标明意义的函数,其定义域一般是指使函数表达式有意义的自变量的取值范围。
例如: f ( x ) = 1 − x 2 f(x)=\sqrt{1-x^2} f(x)=1−x2,这个函数的定义域就是 x ∈ [ − 1 , 1 ] x\in[-1,1] x∈[−1,1],解两个不等式就可以了。
( 3 ) (3) (3) 我们给出的函数定义只有一个自变量,因此称之为一元函数,并且对于自变量 x x x 在定义域内的每一个值,因变量 y y y 总有唯一一个确定的值与之对应,这样的函数称为但是函数。以后,在没有特殊说明的情况下,我们讨论的函数均为单值函数。
( 4 ) (4) (4) 函数的表示方式常用的有三种(这个好像初中就学过),即为表格法(如上面例子),解析法和图像法(如下图)。
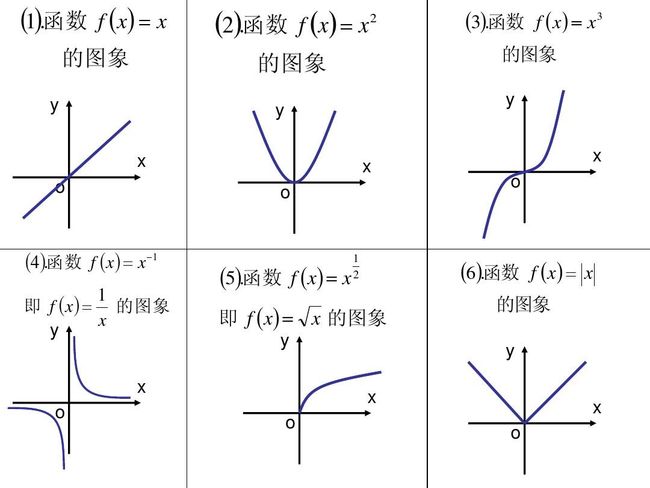
我们在写题目的过程中还会遇到这样的函数:
1. 符号函数 1.符号函数 1.符号函数
y = s g n ( x ) = { 1 x > 0 0 x = 0 − 1 x < 0 \begin{equation} y=sgn(x)=\left\{ \begin{array}{rr} 1 & {x > 0}\\ 0 & {x=0}\\ -1 &{x<0}\\ \end{array} \right. \end{equation} y=sgn(x)=⎩ ⎨ ⎧10−1x>0x=0x<0
2. 绝对值函数 2.绝对值函数 2.绝对值函数
y = ∣ x ∣ = { x x > 0 0 x = 0 − x x < 0 \begin{equation} y=|x|=\left\{ \begin{array}{rr} x & {x > 0}\\ 0 & {x=0}\\ -x &{x<0}\\ \end{array} \right. \end{equation} y=∣x∣=⎩ ⎨ ⎧x0−xx>0x=0x<0
这种 分段函数 也是需要我们注意的。
另外,再补充一个吧:取整函数和取小数部分的函数:
取整函数: f ( x ) = [ x ] f(x)=[x] f(x)=[x]
取小数函数: f ( x ) = f(x)= f(x)= { x x x}
课后习题:(答案会在下一期公布)
( 1 ) (1) (1) 求下列函数的定义域:
1. 1. 1. f ( x ) = 1 x 2 − 3 x − 4 f(x)=\displaystyle \frac 1 {x^2-3x-4} f(x)=x2−3x−41
2. 2. 2. f ( x ) = 2 − x + l o g 2 ( x − 1 ) f(x)=\sqrt{2-x}+log_2(x-1) f(x)=2−x+log2(x−1)
( 2 ) (2) (2) 下列函数是否相同?
1. 1. 1. f ( x ) = ln x 2 , g ( x ) = 2 ln x f(x)=\ln x^2,g(x)=2 \ln x f(x)=lnx2,g(x)=2lnx
2. 2. 2. f ( x ) = ( x − 1 ) 2 , g ( x ) = ∣ x − 1 ∣ f(x)=\sqrt{(x-1)^2},g(x)=|x-1| f(x)=(x−1)2,g(x)=∣x−1∣
我们下一期再见吧!
由于作者太菜,欢迎大家在评论区指出作者的错误哦!
点个赞吧。