嵌入式算法——傅里叶变换算法
文章引注
https://mp.weixin.qq.com/s/5VIpNWci9YLY3m4gcYd6-w
https://blog.csdn.net/jason_sssss/article/details/118933988
摘要
傅里叶变换的核心在于,“任何连续周期信号可以由一组适当的正弦曲线组合而成”,在这个基础上对信号的中特定频率的正弦波进行分解或者重组,基于频率方面分析波形。
1、傅里叶变换的意义
近似周期性的方波(红色),可采用6组正弦波(蓝色)合成,这是傅里叶的基础。
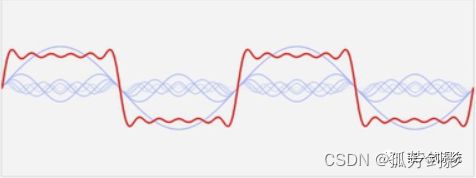
对数字信号处理或者工程数学有一定基础,就明白傅里叶变换的价值。一般情况下的信号或者波形随时间变化,称为时域信号,时域(Time domain)是描述数学函数或物理信号对时间的关系。而以频率和幅度表示信号称为频域,频域(frequency domain)是描述信号在频率方面特性时用到的一种坐标系。其数学理论上暂且不理,针对嵌入式系统开发,只探讨其物理意义或者应用场景。
时域和频域是信号的基本性质,时域的表示较为形象与直观,比较符合一般认知,而频域分析则更为简练,剖析问题更为深刻和方便。
例如下图的左侧时域信号,其可以分解为2路正弦波的叠加效果,右侧为频域信号,表示2路正弦波的频率和幅度。傅里叶变化可简单理解为求解一段信号或波形,由哪些正弦波组成,也可以反向推导多路正弦波合并后的效果。

基于动画形式表现如下:
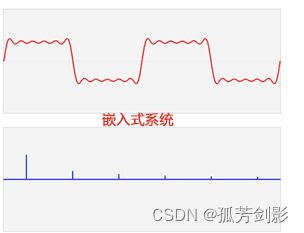
傅里叶变换是一种信号分析方法,让我们对信号的构成和特点进行深入的、定量的研究。把信号通过频谱的方式进行准确的、定量的描述。将原来难以处理的时域信号转换成了易于分析的频域信号,即傅里叶变换的核心是从时域到频域的变换。
2、原理
数字信号属于离散值,对应的称为离散傅里叶变换(DFT),是傅里叶变换在时域和频域上都呈现离散的形式,将时域信号的采样变换为在离散时间傅里叶变换(DTFT)频域的采样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT,也应当将其看作经过周期延拓成为周期信号再作变换。
在实际应用中通常采用快速傅里叶变换以高效计算效率,快速傅里叶变换 FFT(Fast Fourier Transformation)是离散傅里叶变换 DFT(Discrete Fourier Transform)的快速算法。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。同理,从频域到时域的变换,称为逆变换,快速傅里叶逆变换 IFFT和离散傅里叶逆变换IDFT。
(1)快速傅里叶变换(FFT)的优化原理
(2)基-2FFT算法的推导
(3)基-2FFT算法的实现
3、应用
一般嵌入式系统使用快速傅里叶变换是分析某段信号中混合的杂波干扰,或者剔除某个频段后再逆变换。有些高端示波器可以对信号快速傅里叶变换 FFT,直接显示高频杂波的频率或者较大幅度干扰源的频率,以便由针对性的检查电路窜扰。本文主要是讲解使用fft/ifft进行干扰信号的过滤。
(1)基于python生成数据源
1、python生成正弦波,以及混合波形,提取数值作为c语言FFT/IFFT的数据源
2、先进行FFT,输出幅频数据,导入Excel看看效果
3、对数据进行简单过滤
4、过滤后的数据进行IFFT运算,再导入Excel看还原的效果
# This is a Python script.
import numpy as np
import matplotlib.pyplot as plt
def sin_wave(A, f, fs, phi, t):
"""
:params A: 振幅
:params f: 信号频率
:params fs: 采样频率
:params phi: 相位
:params t: 时间长度
# 若时间序列长度为 t=1s,
# 采样频率 fs=1000 Hz, 则采样时间间隔 Ts=1/fs=0.001s
# 采样点个数为 n=t/Ts=1/0.001=1000, 即有1000个点,每个点间隔为 Ts
"""
Ts = 1/fs
n = t / Ts
n = np.arange(n) #生成一个包含从0到n-1的整数的数组,表示时间序列的索引。
y = A*np.sin(2*np.pi*f*n*Ts + phi*(np.pi/180)) #将角度值phi转换为弧度值的
return y
fs = 360*40
my_sin1 = sin_wave(100, 100, fs=fs, phi=0, t=0.08)
my_sin2 = sin_wave(20, 500, fs=fs, phi=0, t=0.08)
my_sin3 = sin_wave(10, 1100, fs=fs, phi=0, t=0.08)
x = np.arange(0, 0.08, 1/fs)
plt.xlabel('x-t (samRate=14400)')
plt.ylabel('y-A')
plt.grid() #用于在绘图时添加网格线
plt.plot(x, my_sin1, 'k--',label="f=100")
plt.plot(x, my_sin2, 'b--',label="f=500")
plt.plot(x, my_sin3, 'g--',label="f=1100")
plt.plot(x, my_sin1+my_sin2+my_sin3, 'r',label="mix")
plt.legend() #用于在图表中添加图例
plt.show()
np.savetxt("sin.txt",my_sin1+my_sin2+my_sin3, fmt='%.06f') #用于将数组数据保存到文本文件
def print_name(name):
print(f'Hi, {name}')
if __name__ == '__main__':
print_name('fft test')