双指针算法

算法解释

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。
若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的
区域即为当前的窗口），经常用于区间搜索。
若两个指针指向同一数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是
排好序的。

1.1 归并两个有序数组(88)

题目描述：
给定两个有序数组，把两个数组合并为一个

题解：
从后往前考虑
因为这两个数组已经排好序，我们可以把两个指针分别放在两个数组的末尾，即 nums1 的 m − 1 位和 nums2 的 n − 1 位。每次将较大的那个数字复制到 nums1 的后边，然后向前移动一位。因为我们也要定位 nums1 的末尾，所以我们还需要第三个指针，以便复制。

在以下的代码里，我们直接利用 m 和 n 当作两个数组的指针，再额外创立一个 pos 指针，起始位置为 m+n−1。每次向前移动 m 或 n 的时候，也要向前移动 pos。这里需要注意，如果 nums1 的数字已经复制完，不要忘记把 nums2 的数字继续复制；如果 nums2 的数字已经复制完，剩余 nums1 的数字不需要改变，因为它们已经被排好序。

def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
	pos = m+n-1
	m -= 1
	n -= 1
	while m>=0 and n>=0:
		if nums2[n]>=nums1[m]:
			nums1[pos] = nums2[n]
			n -= 1
		else:
			nums1[pos] = nums1[m]
			m -= 1
		pos -= 1
	while n>=0:
		nums1[pos] = nums2[n]
		n -= 1 
		pos -= 1 

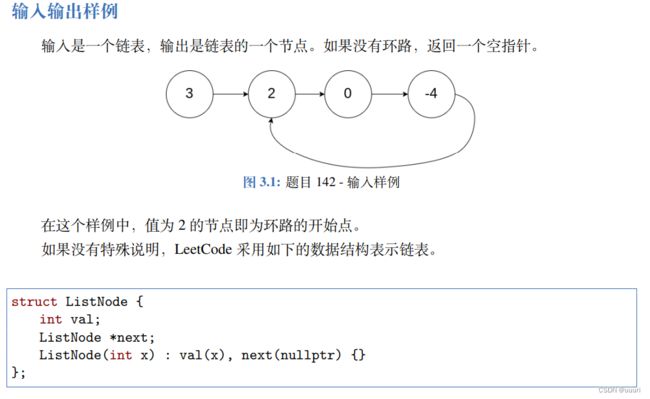
1.2 快慢指针(142)

题目描述：
给定一个链表，如果有环路，找出环路的开始点。

题解：
对于链表找环路的问题，有一个通用的解法——快慢指针（Floyd 判圈法）。
给定两个指针，分别命名为 slow 和 fast，起始位置在链表的开头。每次 fast 前进两步，slow 前进一步。如果 fast可以走到尽头，那么说明没有环路；如果 fast 可以无限走下去，那么说明一定有环路，且一定存在一个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点。

根据：

• f = 2s （快指针每次2步，路程刚好2倍）
• f = s + nb (相遇时，刚好多走了n圈）

推出：s = nb

慢指针从head结点走到入环点需要走 ： a + nb， 而slow已经走了nb，那么slow再走a步就是入环点了。

如何知道slow刚好走了a步？ 从head开始，和slow指针一起走，相遇时刚好就是a步

class Solution(object):
    def detectCycle(self, head):
        fast, slow = head, head
        while 1:
        	if not(fast and fast.next): return
        	fast = fast.next.next
        	slow = slow.next
        	if fast == slow:break
		fast = head
        while fast != slow:
        	fast = fast.next
        	slow = slow.next
        return fast

1.3滑动窗口 76,567,438

滑动窗口 可用于解决一些列的字符匹配问题，典型的问题包括：在字符串 s 中找到一个最短的子串，使得其能覆盖到目标字符串 t。对于目标字符串 t，我们可以在字符串 s 上滑动窗口，当窗口包含 t 中的全部字符后，我们再根据题意考虑能否收缩窗口。

在窗口滑动的过程中，我们可以暴力地统计出窗口中所包含的字符是否满足题目要求，但这没有利用到滑动窗口的基本性质。
事实上，窗口的滑动过程可分解为以下两步基础操作：

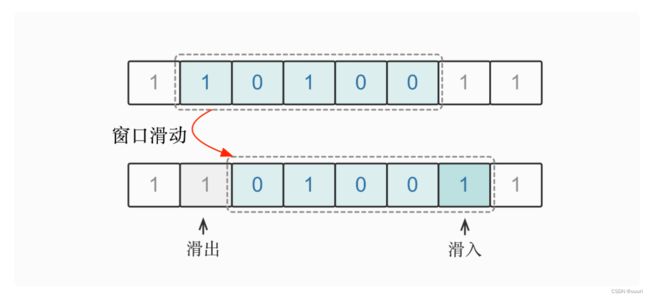
• 窗口右边界往右滑动一位：窗口右端新加入一个字符，但窗口中的其他字符没有发生变化；
• 窗口左边界往右滑动一位：窗口左端滑出一个字符，但窗口中的其他字符没有发生变化。
  因此，我们可以考虑在「一进一出」这样的两个基础操作上做文章。

基于滑动窗口，可解决一系列字符串匹配问题，下面以几个同类的题目为例：

1.3.1 滑动窗口（76,017）

题目描述：
给定两个字符串 S 和 T，求 S 中包含 T 所有字符的最短连续子字符串的长度，同时要求时间
复杂度不得超过$O(n)$。

题解：
我们以哈希表 cnt 记录目标字符串 t 中待匹配的各字符的数目，并在 s 中维护一个变长的滑动窗口，期望使得窗口中的字符能够覆盖 t。需要注意的是，cnt[ch] 可以为负值，且负值表示当前窗口中的字符 ch 过多（多于目标字符 t）。

具体地，设定一个非负变量 need 表示在考虑了窗口中的全部元素后还需要匹配的总字符数目：

1. 当窗口中新加入一位字符 ch 时：

   • 若 cnt[ch]>0，说明 ch 未加入窗口前我们对于字符 ch 还有需求，此时新加入的 ch 能够使得need-1；
   • 若 cnt[ch]]≤0，说明 ch 未加入窗口前我们对于字符 ch 已无需求，此时新加入的 ch 不改变 need。

2. 当窗口中滑出一位字符 ch 时：

   • 若 cnt[ch]>0，说明 ch 未滑出窗口前我们对于字符 ch 仍然还有需求（滑出去需求更大了），此时滑出去的 ch 能够使得 need+1；
   • 若 cnt[ch]=0，说明 ch 未滑出窗口前我们对于字符 ch 刚好无需求（滑出去后会对字符 ch 有需求了），此时滑出去的 ch 能够使得 need+1；
   • 若 cnt[ch]<0，说明 ch 未滑出窗口前我们对于字符 ch 已无需求（过剩），此时滑出去的 ch 不改变 need。

3. 当 need=0 时，说明找到了一个满足题意的窗口，使得中的字符能够覆盖 t。在记录下答案的同时，我们还需要尝试收缩窗口左边界（参照上一步）。

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        if len(s)<len(t):return ''
        cnt = collections.Counter(t)
        left,right = 0,0
        start,end = 0,-1
        need = len(t)
        min_size = len(t)+1
        for right in range(len(s)):
        	ch = s[right]
        	if ch in cnt:
        		if cnt[ch] >0:
        			need -= 1
        		cnt[ch] -= 1
        		
        while need == 0:
        	if right-left+1 < min_size:
        		min_size = right-left+1
        		start,end = left,right
        	ch = s[left]
        	if ch in cnt:
	        	if cnt[ch] >=0:
	        		need +=1
	        	cnt[ch] +=1
	        left +=1
	    return s[start,end+1]

1.3.2 变长滑动窗口：数组

最短超串(面试题17.18)
题目描述：
假设你有两个数组，一个长一个短，短的元素均不相同。找到长数组中包含短数组所有的元素的最短子数组，其出现顺序无关紧要。

返回最短子数组的左端点和右端点，如有多个满足条件的子数组，返回左端点最小的一个。若不存在，返回空数组。
结题思路：
与上面两题相同都是运用滑动窗口

class Solution:
    def shortestSeq(self, big: List[int], small: List[int]) -> List[int]:
        cnt = collections.Counter(small)
        min_size = len(big)+1
        start,end = 0,-1
        left,right = 0,0
        need = len(small)
        for right in range(len(big)):
            k = big[right]
            if k in cnt:
                if cnt[k]>0:
                    need-=1
                cnt[k]-=1
            while need ==0:
                if right-left+1<min_size:
                    min_size = right-left+1
                    start,end = left,right
                k = big[left]
                if k in cnt:
                    if cnt[k]>=0:
                        need+=1
                    cnt[k]+=1
                left+=1
            
        return [start,end] if min_size!= len(big)+1 else []

1.3.3 定长滑动窗口：异位词

字符串的排列(567)
题目描述：
给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串 。

结题思路：
本题与 76. 最小覆盖子串 和 剑指 Offer II 017. 含有所有字符的最短字符串 是类似的，最大的不同在于本题要求滑动窗口是 固定长度 的。

例如，对于s1 = “ab”，我们要在s2 = "eidbaooo"中找到一个与s1同样长度的子字符串 s’使得其中各元素的数目与s1保持一致（即 s’ 与 s1 为「异位词」）。

借用下面两道题目中的表述: 「异位词」指字母相同，但排列不同的字符串。

因此，在窗口滑动的过程中，我们维持一个长度为 len(s1) 的滑动窗口，当窗口中待匹配的字符数目为 0 我们就找到了一个满足要求的子串。

class Solution:
    def checkInclusion(self, s1: str, s2: str) -> bool:
        if len(s1)>len(s2):return False
        s1 = sorted(s1)
        need = len(s1)
        cnt = collections.Counter(s1)
        for right in range(len(s2)):
        	ch = s2[right]
        	if ch in cnt:
        		if cnt[ch]>0:
        			need -=1
        		cnt[ch] -=1
        	left = right-len(s1)
        	if left>=0:
        		ch = s2[left]
        		if ch in cnt:
        			if cnt[ch]>=0:
        				need +=1
        			cnt[ch]+=1
        	if need ==0:return True
        return False

1.3.4 定长滑动窗口：异位词的位置

找到字符串中所有字母异位词(438)
题目描述：
给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

解题思路：
本题则在上述两题 567. 字符串的排列 的基础上记录下满足要求的定长滑动窗口的左端点。

因此，在窗口滑动的过程中，我们维持一个长度为 len§ 的滑动窗口，当窗口中待匹配的字符数目为 need=0 时我们就找到了一个满足要求的子串，记录下此时窗口的左端点即可。

在上述代码的基础上，增加窗口左边界的记录即可。

class Solution:
    def findAnagrams(self, s: str, p: str) -> List[int]:
        
        n, m = len(s), len(p)
        if m > n:
            return []
        
        cnt = collections.Counter(p)    # 哈希表：记录需要匹配到的各个字符的数目
        need = m                        # 记录需要匹配到的字符总数【need=0表示匹配到了】
        res = []

        for right in range(n):
            
            # 窗口右边界
            ch = s[right]               # 窗口中新加入的字符
            if ch in cnt:               # 新加入的字符位于p中
                if cnt[ch] > 0:         # 此时新加入窗口中的字符对need有影响
                    need -= 1
                cnt[ch] -= 1
            
            # 窗口左边界
            left = right - m
            if left >= 0:
                ch = s[left]
                if ch in cnt:           # 刚滑出的字符位于p中
                    if cnt[ch] >= 0:    # 此时滑出窗口的字符对need有影响
                        need += 1
                    cnt[ch] += 1

            if need == 0:           # 每次找到一个满足题意的窗口，其左端点为right-m+1
                res.append(right - m +1)
        
        return res

练习

1.4 验证回文串Ⅱ(680)

题目描述：
给你一个字符串 s，最多 可以从中删除一个字符。

请你判断 s 是否能成为回文字符串：如果能，返回 true ；否则，返回 false 。

解题思路：
首先考虑如果不允许删除字符，如何判断一个字符串是否是回文串。常见的做法是使用双指针。定义左右指针，初始时分别指向字符串的第一个字符和最后一个字符，每次判断左右指针指向的字符是否相同，如果不相同，则不是回文串；如果相同，则将左右指针都往中间移动一位，直到左右指针相遇，则字符串是回文串。

在允许最多删除一个字符的情况下，同样可以使用双指针，通过贪心实现。
初始化两个指针 $low$和 $high$ 分别指向字符串的第一个字符和最后一个字符。每次判断两个指针指向的字符是否相同:

• 如果相同，则更新指针，将 $low$ + 1，$high$ - 1，然后判断更新后的指针范围内的子串是否是回文字符串。
• 如果两个指针指向的字符不同，则两个字符中必须有一个被删除，此时我们就分成两种情况：
  • 即删除左指针对应的字符，留下子串 s[$low+1:high$]，
  • 或者删除右指针对应的字符，留下子串 s[$low:thigh-1$]。

当这两个子串中至少有一个是回文串时，就说明原始字符串删除一个字符之后就以成为回文串。

class Solution:
    def validPalindrome(self, s: str) -> bool:
		def checkPalindrome(low,high):
			while low<high:
				if s[low] != s[high]:return False
				low+=1
				hight -=1
			return True
		low,high = 0,len(s)-1
		while low<high:
			if s[low] != s[high]:
				return checkPalindrome(low+1,high) or checkPalindrome(low,high-1)
			low+=1
			high-=1
		return True

1.5 通过删除字母匹配到字典里最长的单词(524)

题目描述：
给你一个字符串 s 和一个字符串数组 dictionary ，找出并返回 dictionary 中最长的字符串，该字符串可以通过删除 s 中的某些字符得到。

如果答案不止一个，返回长度最长且字母序最小的字符串。如果答案不存在，则返回空字符串。

解题思路：
根据题意，我们需要解决两个问题：

• 如何判断 $dictionary$ 中的字符串 t 是否可以通过删除 s 中的某些字符得到；

• 如何找到长度最长且字典序最小的字符串。

1. 第 1 个问题实际上就是判断 t 是否是 s 的子序列。因此只要能找到任意一种 t 在 s 中出现的方式，即可认为 t 是 s 的子序列。而当我们从前往后匹配时，可以发现每次贪心地匹配最靠前的字符是最优决策。

假定当前需要匹配字符 c,而字符 c 在 s 中的位置 $x_1$和 $x_2$​出现（$x_1<x_2$）,那么贪心取
$x_1$是最优解，因为 $x_2$后面能取到的字符，$x_1$也都能取到，并且通过 $x_1$与
$x_2$之间的可选字符，更有希望能匹配成功。

这样，我们初始化两个指针 i 和 j，分别指向 t 和 s 的初始位置。每次贪心地匹配，匹配成功则 i 和 j 同时右移，匹配 t 的下一个位置，匹配失败则 j 右移，i 不变，尝试用 s 的下一个字符匹配 t。

最终如果 i 移动到 t 的末尾，则说明 t 是 s 的子序列。

2. 第 2 个问题可以通过遍历 $dictionary$ 中的字符串，并维护当前长度最长且字典序最小的字符串来找到。

def findLongestWord(self, s: str, dictionary: List[str]) -> str:
	res = ''
	length = len(s)
	for c in dictionary:
		i,j =0,0
		while i<len(c) and j<length:
			if c[i] == s[j]:
				i+=1
			j+=1	
		if i == len(c):
			if len(c)>len(res) or(len(c)==res and c<res):
				res = c
	return c