15哈夫曼树/哈夫曼编码
文章目录
- 哈夫曼树的基本概念
- 哈夫曼树的特点
- 哈夫曼树的构造算法
-
- 1. 哈夫曼树的构造过程
- 代码实现
- 哈夫曼编码
-
- 文件的编码和解码
哈夫曼树的基本概念
哈夫曼树又称为最优树,作用是找到一种效率最高的判断树。
-
路径:从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
-
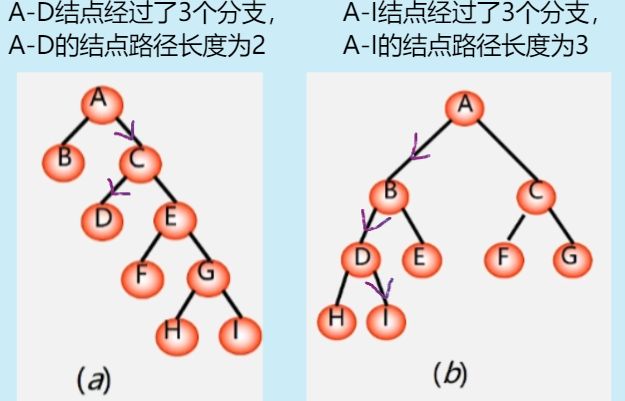
结点的路径长度:两结点间路径上的分支树
- 如图 a :从 A - D 的路径长度就是是 2。从 A 到 B C D E F G F I 的路径长度分别为 1 1 2 2 3 3 4 4
- 如图 b:从 A 到 B C D E F G H I 的路径长度分别为 1 1 2 2 2 2 3 3。
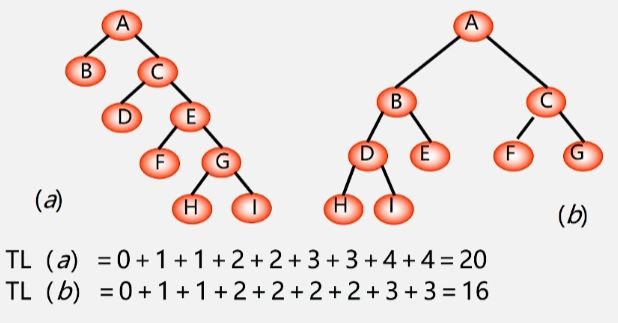
- 树的路径长度:从树根到每一个结点的路径长度之和称为树的路径长度。
- 记作:TL(根节点到它自身的结点路径长度为0)
- 结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树,但是路径长度最短的不一定是完全二叉树。
- 权(weight):将树中结点赋个一个有着某种含义的数值,则称这个数值为该
结点的权。
- **结点的带权路径长度:**从根结点到该结点之间的路径长度与该结点的权的乘积。
- 如前言中的树中的 小于60分的人数占比 X 到该分支的判断次数( 5 % X 3,)5%是权,3 是路径长度。
- 树的带权路径长度:树中所有叶子结点的带权路径之和。
- **哈夫曼树:**树的带权路径长度(WPL)最短的树。
- 带权路径长度最短是在树的度相同的树中比较而得到的结果,因此有最优二叉树,最优三叉树之称等等。
- 最优二叉树:树的带权路径长度(WPL)最短的二叉树。
哈夫曼树的特点
权值越大的结点离根节点越近,权值越小的结点离根节点越远,能使总路径越短。
- 满二叉树不一定是哈夫曼树。
- 具有相同带权节点的哈夫曼树不唯一,如上图的 3树和4树,都是哈夫曼树但并不是同一棵树。
哈夫曼树的构造算法
贪心算法
- 构造哈夫曼树时首选选择权值小的叶子结点。
- 这样就可以将权值大的叶子放到后面构造,大的留在最后就可以离根近一些。
1. 哈夫曼树的构造过程
- 根据 n 个给定的权值 {W₁,W₂,W₃…,Wn} 构成n棵二叉树的森林 F = {T₁,T₂,T₃…,Tn},其中 Ti只有一个带权威 Wi的根节点。
- ==构造的森林全是根。==这个森林中,给了几个权值就有几棵树。
- 在森林 F 中选取两棵根节点的权值最小的树作为左右子树,构造一棵新的二叉树,且设置新的二叉树的根节点的权值为其左右子树上根结点的权值之和。
- 选用两小造新树
- 在森林 F 中删除这两棵树,同时将新得到的二叉树加入森林中。
- 删除两小添新人
- 重复上面的 步骤2 和 步骤3,直到森林中只有一棵树为止,这棵树即为哈夫曼树。
- 重复 2、3 剩单根
例如:
有 4 个结点分别是 a b c d 权值分别为 7 5 2 4,试构造哈夫曼树。
- 构造的森林全是根。
- 选用两小造新树。
- 删除两小添新人。
因为构造哈夫曼树的时候是,选用两小造新树。
- 所以:哈夫曼树的结点的度为 0 或 2,没有度为 1 的结点。
- 包含 n 个叶子结点的哈夫曼树中共有 2n -1 个结点。
总结
- 在哈夫曼算法中,初始时有 n 棵二叉树,要经过 n-1 次合并最终成为哈夫曼树。
- 经过 n-1 次合并产生 n-1个新结点,且这 n-1 个新结点都是具有两个孩子的分支结点
- 可见:哈夫曼树中共有 n+n-1 = 2n-1 个结点,且其所有的分支结点的度均不为1
代码实现
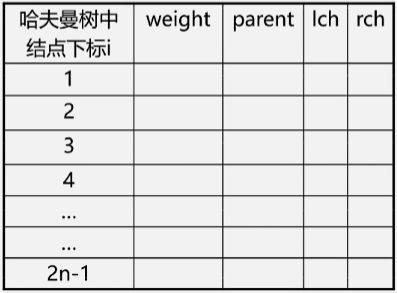
- 采用顺序存储结构——一维结构体数组
- 结点类型定义
typedef struct
{
int weight;//结点的权重
int parent;//结点的双亲
int lchild,rchild;//结点的左、右孩子下标
}HuffmanTree;//动态分配数组存储哈夫曼树
- 哈夫曼树一共有n个叶子结点,和n-1个非叶子结点,因此结点总数为2n-1个。如果使用顺序存储方式来实现哈夫曼树,那么需要开辟一个大小为2n的数组来存储所有的结点,其中0下标不用。
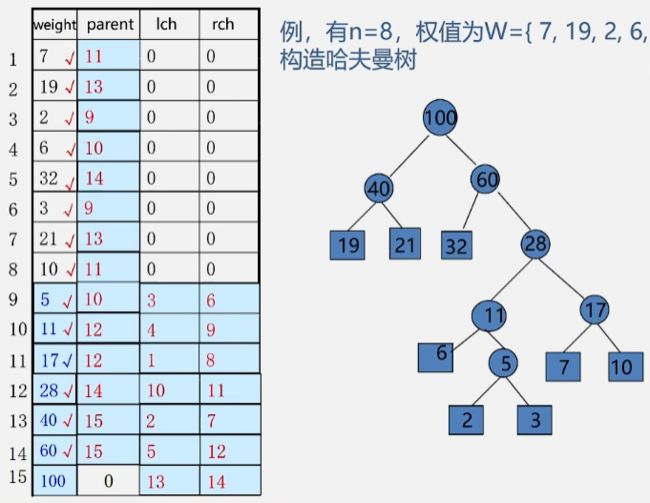
- 有 8 个权值为 W ={7,19,2,6,32,3,21,10} 的叶子结点,构造哈夫曼树。
- 这棵哈夫曼树则有 2n-1=2x8-1=15 个结点。
- 那么现在就应该构造有 2n = 2x8= 16 个元素的数组。
假设有如下n个权值:7、5、2、4、8、3。
- 开辟一个大小为2n-1的数组ht,用于存储所有的节点,初始化所有节点的parent、left、right属性为0。
- 初始化前n个节点为叶子节点,并把它们的权值存入权值数组weights中。
- 对于所有的叶子节点,创建一个长度为n的编码数组hc,并将所有元素初始化为0。
- 依次选择权值最小的两个节点,将它们合并成一个新的节点,并将它们的父节点设置为新的节点,并把新节点的权值设置为两个子节点的权值之和。
- 将新节点存入数组ht中,并将新节点的下标作为其左右孩子节点的父节点。
- 重复步骤4和5,直到所有节点都合并成一个根节点为止。
#include
#include
#include
/*这个是用了第0下标的代码*/
#define MaxSize 1000 //定义最大结点数
//结点结构体
typedef struct Node{
int weight ; //权值
int parent ; //父节点下标
int left_child ; //左子节点下标
int right_child; //右子结点下标
}Node;
//哈夫曼树结构体
typedef struct HuffmanTree{
int n; //节点数
Node nodes[MaxSize]; //结点数组
}HuffmanTree;
//选择两个权值最小的结点
void select_min_two(HuffmanTree *ht,int *p1, int *p2)
{
int i;
int w1=INT_MAX,w2=INT_MAX; //初始化为最大值
*p1=*p2=-1; //初始化为无效值
for (i = 0; i< ht->n; i++)
{ // 如果当前节点是没有父节点的,且它的权重比当前最小值还要小
if (ht->nodes[i].parent == -1) //未被选择
{
if(ht->nodes[i].weightnodes[i].weight; // 更新最小值
}
else if(ht->nodes[i].weightnodes[i].weight; // 更新次小值
}
}
}
}
//构造哈夫曼树
void build_huffman_tree(HuffmanTree *ht,int *weights,int n)
{
int i,p1,p2;
if(n>MaxSize) // 节点数不能超过最大值
{
printf("Too many nodes");
return ;
}
if (n == 1) { // 如果只有一个节点,构建一个单节点树
ht->n = 1;
ht->nodes[0].weight = weights[0];
ht->nodes[0].parent = -1;
ht->nodes[0].left_child = -1;
ht->nodes[0].right_child = -1;
return;
}
ht->n=n; // 节点数等于叶子节点数
// 初始化叶子节点
for (i = 0; i < n; i++) {
ht->nodes[i].weight = weights[i];
ht->nodes[i].parent = -1;
ht->nodes[i].left_child = -1;
ht->nodes[i].right_child = -1;
}
// 初始化非叶子节点
for (i = n; i < 2 * n - 1; i++) {
ht->nodes[i].weight = 0;
ht->nodes[i].parent = -1;
ht->nodes[i].left_child = -1;
ht->nodes[i].right_child = -1;
}
// 逐步合并节点,构造哈夫曼树
for (i = n; i < 2 * n - 1; i++) {
select_min_two(ht, &p1, &p2); // 选择权值最小的两个节点
ht->nodes[i].weight = ht->nodes[p1].weight + ht->nodes[p2].weight;
ht->nodes[p1].parent = i;
ht->nodes[p2].parent = i;
ht->nodes[i].left_child = p1;
ht->nodes[i].right_child = p2;
}
}
int main() {
int weights[] = {1, 2, 3, 4, 5};
int n = sizeof(weights) / sizeof(weights[0]);
HuffmanTree ht;
build_huffman_tree(&ht, weights, n);
return 0;
}
这是从下标1开始的代码
#include 哈夫曼编码
哈夫曼编码是一种可变长度编码的算法,用于将字符集中的字符映射成不同长度的二进制码。它是一种无损压缩算法,可以有效地压缩文本、音频、图像等数据。
哈夫曼编码的基本思想是,为频繁出现的字符分配较短的编码,为不频繁出现的字符分配较长的编码。这样做可以使得编码后的数据具有更高的压缩率。具体来说,哈夫曼编码的过程如下:
- 统计字符集中每个字符出现的频率
- 将每个字符及其频率构成一个叶子结点,构建一颗哈夫曼树。哈夫曼树是一种二叉树,每个节点都有两个子节点,除了叶子结点以外,每个节点的权值为其两个子节点的权值之和。
- 从根节点开始遍历哈夫曼树,将左子树编码为0,右子树编码为1,将每个叶子结点的编码记录下来。
- 将每个字符用其对应的编码替换,得到编码后的数据。
由于哈夫曼编码采用可变长度编码,使得频繁出现的字符用较短的编码表示,不频繁出现的字符用较长的编码表示,因此可以达到比固定长度编码更高的压缩率。
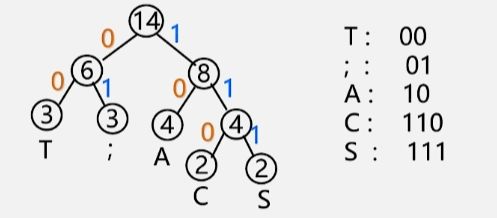
**例:**要传输的字符集 D = {C,A,S,T,; }(注意这个分号也是,并没有多打),每个字符出现的频率 W = {2,4,2,3,3}。
哈夫曼编码的两个问题
- 为什么哈夫曼编码能够保证是前缀编码?
- 因为没有一片叶子是另一片叶子的祖先,所以每个叶子结点的编码就不可能是其他叶子结点编码的前缀。
- 为什么哈夫曼编码能够保证字符编码总长最短?
- 因为哈夫曼树就是树的带权路径长度最短的树,所以整个字符编码的总长最短。
#include
#include
#include
// 哈夫曼树结构体定义
typedef struct Node {
char character; // 字符
int frequency; // 频率
struct Node *left, *right;
} Node;
// 函数声明
Node *createNode(char character, int frequency);
Node **createPriorityQueue(int size);
void insertPriorityQueue(Node **queue, Node *node, int size);
Node *removeSmallestPriorityQueue(Node **queue, int size);
Node *buildHuffmanTree(char *characters, int *frequencies, int size);
void printHuffmanCodes(Node *root, int *arr, int top);
int main() {
// 示例字符及频率
char characters[] = {'a', 'b', 'c', 'd', 'e', 'f'};
int frequencies[] = {5, 9, 12, 13, 16, 45};
int size = sizeof(characters) / sizeof(characters[0]);
// 创建哈夫曼树
Node *root = buildHuffmanTree(characters, frequencies, size);
// 输出哈夫曼编码
int arr[100], top = 0;
printf("Huffman Codes:\n");
printHuffmanCodes(root, arr, top);
return 0;
}
// 创建结点函数
Node *createNode(char character, int frequency) {
Node *node = (Node *)malloc(sizeof(Node));
node->character = character;
node->frequency = frequency;
node->left = node->right = NULL;
return node;
}
// 创建优先级队列(按频率升序)
Node **createPriorityQueue(int size) {
Node **queue = (Node **)malloc(size * sizeof(Node *));
for (int i = 0; i < size; i++) {
queue[i] = NULL;
}
return queue;
}
// 插入优先级队列
void insertPriorityQueue(Node **queue, Node *node, int size) {
int i;
for (i = 0; i < size; i++) {
if (queue[i] == NULL || queue[i]->frequency > node->frequency) {
break;
}
}
for (int j = size - 1; j > i; j--) {
queue[j] = queue[j - 1];
}
queue[i] = node;
}
// 移除优先级队列中最小元素
Node *removeSmallestPriorityQueue(Node **queue, int size) {
Node *smallest = queue[0];
for (int i = 0; i < size - 1; i++) {
queue[i] = queue[i + 1];
}
queue[size - 1] = NULL;
return smallest;
}
// 构建哈夫曼树
Node *buildHuffmanTree(char *characters, int *frequencies, int size) {
// 创建优先级队列
Node **queue = createPriorityQueue(size);
int i;
for (i = 0; i < size; ++i) {
queue[i] = createNode(characters[i], frequencies[i]);
}
// 构建哈夫曼树
while (i > 1) {
// 从优先级队列中移除两个最小频率的节点
Node *left = removeSmallestPriorityQueue(queue, i);
Node *right = removeSmallestPriorityQueue(queue, --i);
// 创建一个新节点,左右子节点分别是两个最小频率的节点
Node *internalNode = createNode('\0', left->frequency + right->frequency);
internalNode->left = left;
internalNode->right = right;
// 将新节点插入优先级队列
insertPriorityQueue(queue, internalNode, i);
--i;
}
// 返回哈夫曼树的根节点
Node *root = queue[0];
free(queue);
return root;
}
// 输出哈夫曼编码
void printHuffmanCodes(Node *root, int *arr, int top) {
if (root->left) {
arr[top] = 0;
printHuffmanCodes(root->left, arr, top + 1);
}
if (root->right) {
arr[top] = 1;
printHuffmanCodes(root->right, arr, top + 1);
}
// 到达叶子节点,打印编码
if (!root->left && !root->right) {
printf("%c: ", root->character);
for (int i = 0; i < top; ++i) {
printf("%d", arr[i]);
}
printf("\n");
}
}
文件的编码和解码
等长编码
- 如果使用的是之前的等长编码对这段明文进行编译的话,就需要占用3024bit的空间
哈夫曼编码
- 而用哈夫曼编码则能够节省将近一半的空间
- 能通过编码将字符转换成一堆二进制码,同样的也能通过解码将这一堆二进制码转换成人能看得明白的文字
编码过程:
- 频率统计:读取文件内容,统计每个字符出现的频率。例如,文件内容为"ABRACADABRA",则字符频率统计结果为:A-5,B-2,C-1,D-1,R-2。
- 创建哈夫曼树节点:为每个字符创建一个哈夫曼树节点,并将它们按照频率从小到大放入优先队列(最小堆)中。如:C(1),D(1),B(2),R(2),A(5)。
- 构建哈夫曼树:
- 取出C(1)和D(1),合并为新节点CD(2),将CD(2)插入队列:B(2),R(2),CD(2),A(5)。
- 取出B(2)和R(2),合并为新节点BR(4),将BR(4)插入队列:CD(2),A(5),BR(4)。
- 取出CD(2)和A(5),合并为新节点CDA(7),将CDA(7)插入队列:BR(4),CDA(7)。
- 取出BR(4)和CDA(7),合并为新节点BRCDA(11),将BRCDA(11)插入队列。
- 此时队列中只有一个节点BRCDA(11),这就是哈夫曼树的根节点。
- 生成哈夫曼编码表:遍历哈夫曼树,得到每个字符的编码:
- A: 0
- B: 110
- C: 1010
- D: 1011
- R: 111
- 编码文件:根据哈夫曼编码表,将原文件内容替换为相应的二进制编码:
- ABRACADABRA -> 011011101010110010100110110
解码过程:
- 读取编码文件:将编码后的文件(011011101010110010100110110)加载到内存中。
- 解码:
- 从哈夫曼树的根节点开始遍历,根据二进制内容的每个位来决定向左(0)或向右(1)走。
- 例如,二进制内容的第一位是0,从根节点向左走,到达A节点,将A写入解码后的文件。
- 继续解析,接下来的二进制位是1,从根节点向右走,接着是1,继续向右走,最后是0,向左走,到达B节点,将B写入解码后的文件。
- 重复这个过程,直到所有二进制内容都被解析完。最终得到的解码后的文件内容为"ABRACADABRA",与原始文件内容相同。
通过这个解码过程,我们成功地还原了原始文件的内容。这就是哈夫曼编码的无损解压缩过程。