数据挖掘-k近邻算法的R实现

本次为学生时期所写的实验报告，代码程序为课堂学习和自学，对网络程序有所参考，如有雷同，望指出出处，谢谢！

基础知识来自教材：李航的《统计学习方法》

本人小白，仍在不断学习中，有错误的地方恳请大佬指出，谢谢！

一、代码实现（R语言）

1.编写函数使用k近邻算法计算预测值

myknn <- function(train.data, ytrain, test.data, K=3, distance = 'euclidean'){ 
  #输入训练数据集和测试数据集数据，默认给定k值为3，默认距离函数使用欧氏距离
  testlen = nrow(test.data)   #测试数据集的行数
  trainlen = nrow(train.data) #训练数据集的行数
  
  A = rbind(test.data,train.data) #A为测试数据集和训练数据集按行合并形成的矩阵
  
  dist = dist(A,method = distance)
  testdist = as.matrix(dist)[1:testlen,(testlen+1):(testlen+trainlen)]       
  #将dist变换为矩阵形式，并取适当的行和列，使得第（i，j）元素为测试数据集第i行向量与训练数据集第j行向量的距离
  
  colnames(testdist) = c(1:trainlen)  #更改列编号为从1开始
  
  ytest = rep(NA,testlen)   
                           #建立长度与测试数据集等长的空向量，用于存储测试数据集对应的y的预测值
  for (i in 1:testlen) {
testsorted = sort(testdist[i,],index.return = TRUE)  
                              #将距离矩阵的第i行按从小到大排列，并返回排序后对应于原序列的下标
    
reindex = testsorted$ix[1:K]  
                                      #返回与第i行测试数据距离最近的前K个训练数据对应的原下标
    
    #接下来寻找下标对应的y值中出现频率最大的y值
    uniqve = unique(ytrain[reindex])        #去掉下标对应的y值中重复的值
match = match(ytrain[reindex],uniqve)     
                                            #找出ytrain[reindex]中每个元素在uniqve中的位置
    tabulate = tabulate(match)              #记录match从1开始的数字中各数字出现的次数
    max = which.max(tabulate)               #找出tabulate中最大的数
    
    ytest[i]=uniqve[max] 
  }
  
  ytest
}

2.使用交叉验证方法选择参数K

#对K值进行选择：使用交叉验证的办法
findk <- function(X,y,K.list,S=5){   #S表示交叉验证中的折数（S-折交叉验证）
  
  nk = length(K.list)
  
  #进行数据分组
  n = dim(X)[1]   #数据的行数
  CV.ID = sample(rep(1:S,length.out = n))  
                          #进行1到S的循环，总长度为n（如1,2,3,4,1,2,3,4,1,2...），并进行打乱
  CV.per = matrix(NA,nk,S)#交叉验证的下标
  for (i in 1:nk) {
    for (j in 1:S){
      X.test = X[CV.ID==j,] 
                             #相当于从被分为S份的数据中随机抽取1份作为测试数据集，循环S次
      y.test = y[CV.ID==j]
      X.train = X[CV.ID!=j,] 
                            #相当于从被分为S份的数据中随机抽取（S-1）份作为训练数据集，循环S次
      y.train = y[CV.ID!=j]
      
      y.hat =myknn(X.train, y.train, X.test,K = K.list[i], distance = 'euclidean')  
                            #测试数据集中y的预测值
      y.test = as.numeric(y.test)
      y.hat = as.numeric(y.hat)  #将向量转化为数值型
      
      CV.per[i,j] = mean((y.test-y.hat)^2)
    }
  }
  
  CV.per.mean = apply(CV.per, 1, mean)  #将各K值对应的交叉验证误差存储在此向量中

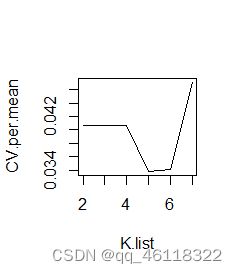
  plot(K.list,CV.per.mean,type="l") #绘制k值与对应误差值的函数图，可用于直观判断k值的最佳取值

  K.opt = K.list[which.min(CV.per.mean)]
  list(CV.per=CV.per, CV.per.mean=CV.per.mean, K.opt=K.opt)
  
}

二、检验

1.检验数据选择

本次实验使用UCI数据库中Iris数据集：

（1）该数据集的特征量有：萼片长度（厘米）、萼片宽度厘米、花瓣长度厘米、花瓣宽度厘米；

（2）类别有：鸢尾花Iris Setosa、鸢尾花Iris Versicolour、弗吉尼亚鸢尾 Iris Virginica；

（3）不同类别的话所对应的各特征值的数据有所不同。从中抽取部分作为测试数据集，剩下的作为训练数据集，可使用knn算法计算测试数据对应的类，并与实际值进行对比。

2.检验代码编写

（1）使用交叉验证法寻找合适k值

输入：

#载入数据
data <- read.csv("F:/iris.data")
data=as.matrix(data)  #将数据框转化为矩阵格式
X = data[,1:4]
y = data[,5]

#将y中的因子都转化为数值型：0代表Iris Setosa；1代表Iris Versicolour；2代表Iris Virginica
for (i in 1:length(y)){
  if (y[i]=="Iris-setosa"){
    y[i]=0
  }else if(y[i]=="Iris-versicolor"){
    y[i]=1
  }else if(y[i]=="Iris-virginica"){
    y[i]=2
  }
}

#使用上述函数寻找合适k值
K.list=c(2,3,4,5,6,7)
findk(X,y,K.list)

输出：

> findk(X,y,K.list)
$CV.per
           [,1] [,2]       [,3]       [,4]       [,5]
[1,] 0.03333333    0 0.06666667 0.00000000 0.10344828
[2,] 0.03333333    0 0.06666667 0.00000000 0.10344828
[3,] 0.03333333    0 0.06666667 0.00000000 0.10344828
[4,] 0.06666667    0 0.03333333 0.00000000 0.06896552
[5,] 0.03333333    0 0.03333333 0.00000000 0.10344828
[6,] 0.06666667    0 0.06666667 0.03333333 0.06896552

$CV.per.mean
[1] 0.04068966 0.04068966 0.04068966 0.03379310 0.03402299 0.04712644

$K.opt
[1]5

分析：由图和程序结果可知K取5时可使交叉验证的误差达到最小。

（2）使用knn算法进行预测

 输入：

#（1）随机划分训练数据集和测试数据集
index = sample(rep(1:5,length.out = length(y))) 
X.test = X[index==1,]      #相当于从被分为5份的数据中随机抽取1份作为测试数据集
y.test = y[index==1]
X.train = X[index!=1,]     #相当于从被分为5份的数据中随机抽取4份作为训练数据集
y.train = y[index!=1]

#（2）设置参数K=5，距离使用欧式距离，用K近邻法对测试数据集进行预测
y.hat = myknn(X.train,y.train,X.test,K=5)

#（3）比较预测值与真实值
cbind(y.hat,y.test)

#（4）计算正确分类概率
percentage = sum(y.hat==y.test)/length(y.test)

输出：

> cbind(y.hat,y.test)

      y.hat y.test

 [1,] "0"   "0"   

 [2,] "0"   "0"   

 [3,] "0"   "0"   

 [4,] "0"   "0"   

 [5,] "0"   "0"   

 [6,] "0"   "0"   

 [7,] "0"   "0"   

 [8,] "0"   "0"   

 [9,] "0"   "0"   

[10,] "0"   "0"   

[11,] "0"   "0"   

[12,] "1"   "1"   

[13,] "1"   "1"   

[14,] "1"   "1"   

[15,] "2"   "1"   

[16,] "1"   "1"   

[17,] "2"   "1"   

[18,] "1"   "1"   

[19,] "1"   "1"   

[20,] "1"   "1"   

[21,] "2"   "2"   

[22,] "2"   "2"   

[23,] "2"   "2"   

[24,] "2"   "2"   

[25,] "2"   "2"   

[26,] "2"   "2"   

[27,] "2"   "2"   

[28,] "2"   "2"   

[29,] "2"   "2"   

[30,] "2"   "2"   

> percentage

[1] 0.9333333

分析：可得输出结果如上所示，将误分类数据进行标亮，可知共有两个数据点被误分类，其他分类正确。正确分类概率为93.3%

三、小结

本次实验主要编写了k近邻算法的程序，以及使用所学的交叉验证法对参数k进行选择。程序编写关键在与对k近邻算法的理解，该算法没有显式函数，而是依靠距离最近的k个数据点根据分类决策规则进行类别的判断。k的取值十分重要，若k取值过小，则模型近似误差减小，但同时模型变得较为复杂，结果将会有较大波动，方差变大；若k取值过大，则预测值较稳定，但同样的近似误差也将增大，预测有更大的偏差。因此编写k参数选择的程序是十分有必要的。此外，距离函数的选定也会对k近邻法预测的值产生一定影响。