【数据结构】二叉树链式存储结构

目录

一、基础知识

二、二叉树的遍历

1 前序、中序以及后序遍历

1.1. 前序遍历

1.2. 中序遍历

1.3 后序遍历

练习：请写出下面的前序/中序/后序/层序遍历

2 层序遍历

流程

三、节点个数以及高度等

1.二叉树节点个数

2.二叉树叶子节点个数

3.二叉树的高度

4.二叉树第k层节点个数

5.二叉树查找值为x的节点

6.测试的流程

四、完全二叉树检测

五、创建二叉树

六、实战OJ

---

一、基础知识

手动快速创建一棵简单的二叉树，快速进入二叉树 操作学习

注意：这只是当你需要一颗简单二叉树时的操作，并不是二叉树真正的创建方式

// 注意：下述方式并不是创建二叉树的真正方式，此处为了方便学习构造树
BTNode* BinaryTreeCreate()
{
	BTNode* node1 = BuyBTNode(1);
	BTNode* node2 = BuyBTNode(2);
	BTNode* node3 = BuyBTNode(3);
	BTNode* node4 = BuyBTNode(4);
	BTNode* node5 = BuyBTNode(5);
	BTNode* node6 = BuyBTNode(6);

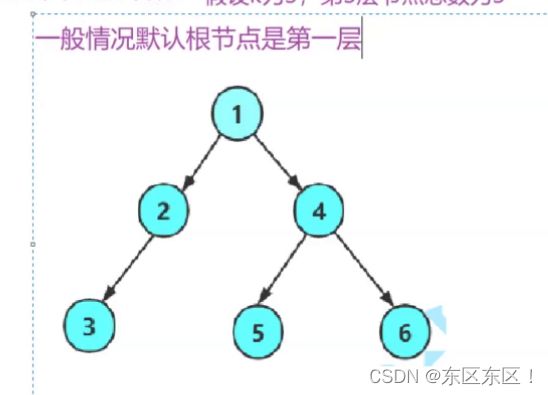
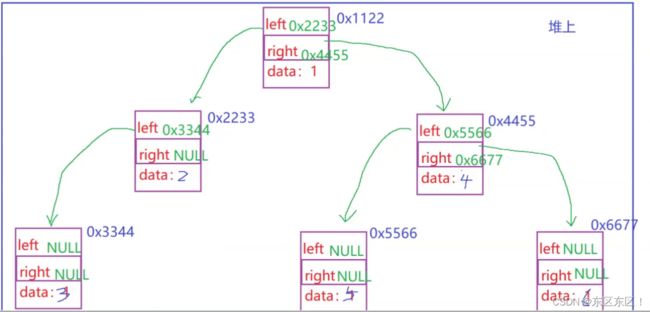
	node1->left = node2;
	node1->right = node4;

	node2->left = node3;

	node4->left = node5;
	node4->right = node6;

	return node1;
}

二、二叉树的遍历

1 前序、中序以及后序遍历

        学习二叉树结构，最简单的方式就是遍历。所谓 二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

       访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础

按照规则，二叉树的遍历有： 前序/中序/后序的递归结构遍历：

1.1. 前序遍历

(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

void PreOrder(BTNode* root)
{
	if (NULL == root)
		return;

	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

递归前序遍历顺序：  1-  2 - 3 -空 -空- 空 4 - 5 -空 -空- 6

1.2. 中序遍历

(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

上图中序遍历 顺序： 3 2 1  5 6 4

void InOrder(BTNode* root)
{
	if (NULL == root)
		return;

	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

1.3 后序遍历

(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

上图后续遍历顺序 3 2 5 6 4 1

void PostOrder(BTNode* root)
{
	if (NULL == root)
		return;

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

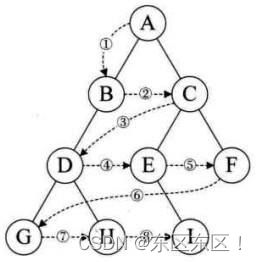
练习：请写出下面的前序/中序/后序/层序遍历

 前序遍历： A B D E H  C F G

中序遍历： D B E H A F C G

后序遍历   D  H E B F G C A

2 层序遍历

       除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。

       设二叉树的根节点所在层数为1 ，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第 2 层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历

假设遍历操作就是将节点中的值域打印出来：

第一层遍历非常简单：

printf("%c", root->val);

注意  此处不能再通过递归方式遍历根的左右子树了，因为通过递归来处理的话是前中序遍历过程，因此只能采用循环来处理，即后续层上的节点只能采用循环来处理

第一层节点遍历完成之后，紧接着要遍历第二层，当在遍历第一层节点时，如果第一层节点有孩子，那么这些孩子节点肯定在第二层

当前n层节点遍历完后，需要遍历第n+1层，要遍历n+1层就要知道n+1层有哪些节点；当在遍历第n层的时候，如果第n层的节点有孩子，那么他的孩子就在n+1层，在遍历n层的时候将他的孩子保存起来即可

流程

空间有个特性：先保存的先遍历

while(主队列不空)

{

1.从队列中取一个节点cur，进行遍历

2.cur有左孩子，保存到队列中

cur有右孩子，保存到队列中

3.将刚遍历的节点从队列中删除掉

}

//层序遍历
void BinaryLevelOrder(BTNode* root)
{
	if (NULL == root)
		return;
	//层序遍历要借助队列
	Queue q;
	QueueInit(&q);
	//1.根节点入队，当队列不空时，循环进行以下操作
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//a.从队头去一个节点,注意QueueFront查找只是将队头元素获取，斌没有将队头元素删除
		struct BTNode* cur = QueueFront(&q);
		//b.将该节点遍历
		printf("%d", cur->data);
		//c.如果cur有左孩子入队列，如果有右孩子入队列
		if (cur->left)
			QueuePush(&q, cur->left);
		if (cur->right)
			QueuePush(&q, cur->right);
		QueuePop(&q);
	}
	QueueDestroy(&q);
	printf("\n");
}

1. 某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为（ a）

A ABDHECFG

B ABCDEFGH

C HDBEAFCG

D HDEBFGCA

2. 二叉树的先序遍历和中序遍历如下：先序遍历： EFHIGJK; 中序遍历： HFIEJKG. 则二叉树根结点为（A）

A E

B F

C G

D H

3. 设一课二叉树的中序遍历序列： badce ，后序遍历序列： bdeca ，则二叉树前序遍历序列为 ___D_ 。

A adbce

B decab

C debac

D abcde

4. 某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列为  A

A FEDCBA

B CBAFED

C DEFCBA

D ABCDEF

三、节点个数以及高度等

1.二叉树节点个数

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (NULL == root)
		return 0;
	 //根为1个节点，递归左子树和右子树
	return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

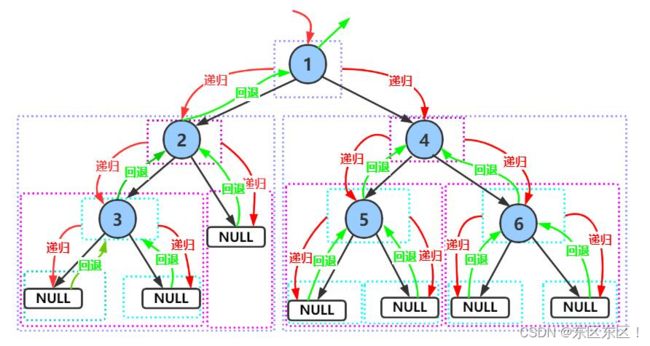
因为根为1个节点，不断递归左子树和右子树，从而求到总的个数

2.二叉树叶子节点个数

结合二叉树概念

叶子节点的个数

实际 = 根的左子树叶子节点个数+ 根右子树叶子节点个数

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	//空树没叶子
	if (NULL == root)
		return 0;

	//既没左节点也没右节点，他就是叶子节点
	if (NULL == root->left && NULL == root->right)
		return 1;

	//左子树多少个叶子+右子树多少个叶子
	return BinaryTreeLeafSize(root->left) +
		BinaryTreeLeafSize(root->right);
}

如上图从1开始往左子树开始判断，到3这个点的时候， 判断3 即没左子树又没有右子树，则return  1，往回递归到1，此时累计为1，开始往1 的右子树判断，到5和6分别return 1，递归到4时累计为2，最终在递归到1点累计叶字节点个数为3. 

3.二叉树的高度

1.空树--》直接返回0

2.非空，可以求子树的高度，在较高子树的基础上+1就是二叉树的高度 

求子树高度的方式和求二叉树的高度方式都是相同的，可以采用递归的方式求子树的高度

//求二叉树的高度
int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	//先求root子树的高度
	int leftHeight = BinaryTreeHeight(root->left);
	int rightHeight = BinaryTreeHeight(root->right);
	
     
	//对左右子树高度进行比较，左子树高就返回左子树并+1，+1是把根算进去
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

 流程：从1开始，root非0，进入左子树2，BinaryTreeHeight(root->left);

root = 2非0，进入左子树3； root = 3非 0，进入左子树null，返回0到3，进入右子树为null

返回0到3，3返回1到2节点，2节点进入右子树为0返回2节点，2节点返回值2到1，1进入右节点4流程相同，最终1节点返回值 3.

4.二叉树第k层节点个数

int BinaryTreeLevelKSize(BTNode* root, int k);

 求 第k层节点个数

1.空树 或者k小于等于0 ，都不用求 直接return 0

2.非空：思考发现，原二叉树的第k层，实际是子树的k-1 层

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (NULL == root  || k <= 0)
		return 0;

	//k=1就是第一层的节点总数1
	if (1 == k)
	{
		return 1;
	}

	//root存在，而且k大于1
	//k到底是多少不知道，直接到root的子树中求k-1层总共有多少个节点即可
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
} 

5.二叉树查找值为x的节点

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, DataType x)
{
    if (NULL == root)
        return NULL;

    //树非空
    //根节点
    if (x == root->data)
        return root;

    //注意或的短路原则
    BTNode* ret;
    (ret = BinaryTreeFind(root->left, x)) ||
        (ret = BinaryTreeFind(root->right, x));

    return ret;
}

这些思路都是一样的，都是采用递归算法，使用时画图理思路即可

6.测试的流程

四、完全二叉树检测

 

int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	int flag = 0;  //标记第一个不饱和的节点
	int CompleteTree = 1;

	//注意：空树也是完全二叉树
	if (NULL == root)
		return 1;
	//1.按照层数遍历找到第一个不饱和的点
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* cur = QueueFront(&q);
		QueuePop(&q);
		if (flag)
		{
			//不饱和节点后所有的节点都不能有孩子
			if (cur->left || cur->right)
			{
				CompleteTree = 0;
				break;
			}
		}
		else
		{
			//检测cur是否饱和
			if (cur->left && cur->right)
			{
				//cur左右孩子都存在
				QueuePush(&q, cur->left);
				QueuePush(&q, cur->right);
			}
			else if (cur->left)
			{
				//只有左孩子没有右孩子
				QueuePush(&q, cur->left);
					flag = 1;
			}
			else if (cur->right)
			{
				//cur只有右孩子没有左孩子
				CompleteTree = 0;
				break;
			}
			else
			{
				//cur左右孩子都不存在，则该节点为第一个不饱和的节点
				flag = 1;
			}
		}
	}
	QueueDestroy(&q);
	return CompleteTree;
}

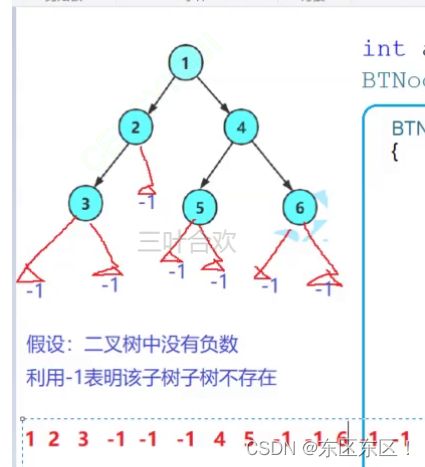
五、创建二叉树

1.如果是空树，直接返回一个NULL
2.非空：
    创建根节点->递归创建根的左子树->递归创建根的右子树
    就是前序遍历的规则

//array保存的是：用户要创建二叉树时节点中值域的集合
BTNode* BinaryTreeCreate(int array[], int size, int* pindex)
{
	

	BTNode* root = NULL;
	//如果二叉树存在，则创建
	if (*pindex < size && array[*pindex] != -1)
	{
		//创建根节点
		root = BuyBTNode(array[*pindex]);

		//递归创建根的左子树
		++(*pindex);
		root->left = BinaryTreeCreate(array, size, pindex);

		//递归创建根的右子树
		++(*pindex);
		root->right = BinaryTreeCreate(array, size, pindex);
	}
	return root;
}

 

六、实战OJ

965 、单值二叉树   OJ

144、二叉树前序遍历   OJ