leetcode刷题笔记——53.最大子数组和

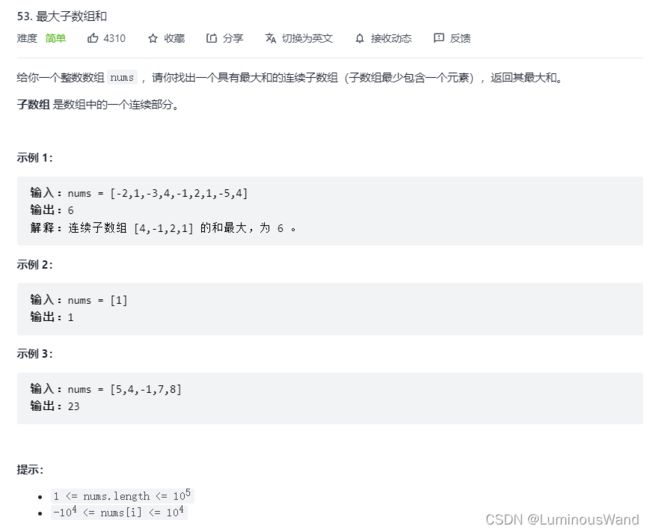
题目描述

分析

贪心

描述

复杂度为O(n)，每输入一个顺序表元素就产生一个状态，全部输入完就产生最终状态。

代码

int maxSubArray(int* nums, int numsSize){
    if(numsSize == 0)
        return nums[0];
    int sum = nums[0],tmpSum=0;
    for(int i=0;i<numsSize;i++){
        tmpSum+=nums[i];
        if(i!=0&&tmpSum>sum){
            sum=tmpSum;
        }
        if(tmpSum<0){
            tmpSum=0;
        }
    }
    return sum;
}

动态规划

描述

由于动态规划我没有学过，因此在此截取leetcode官方题解。

假设nums 数组的长度是 n，下标从 0 到 n-1。

我们用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」，那么很显然我们要求的答案就是：

$$\underset{0\le i\le n-1}{\max }f(i)$$
因此我们只需要求出每个位置的 f(i)，然后返回 f 数组中的最大值即可。那么我们如何求 f(i) 呢？我们可以考虑 nums[i] 单独成为一段还是加入 f(i-1) 对应的那一段，这取决于 nums[i] 和 f(i-1) + nums[i] 的大小，我们希望获得一个比较大的，于是可以写出这样的动态规划转移方程：

$$f(i)=\max \{f(i-1)+nums[i],nums[i]\}$$
不难给出一个时间复杂度 O(n)、空间复杂度 O(n) 的实现，即用一个 f 数组来保存 f(i) 的值，用一个循环求出所有 f(i)。考虑到 f(i) 只和 f(i−1) 相关，于是我们可以只用一个变量 pre 来维护对于当前 f(i) 的 f(i−1) 的值是多少，从而让空间复杂度降低到 O(1)，这有点类似「滚动数组」的思想。

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/maximum-subarray/solution/zui-da-zi-xu-he-by-leetcode-solution/

代码

int maxSubArray(int* nums, int numsSize) {
    int pre = 0, maxAns = nums[0];
    for (int i = 0; i < numsSize; i++) {
        pre = fmax(pre + nums[i], nums[i]);
        maxAns = fmax(maxAns, pre);
    }
    return maxAns;
}

收获

动态规划

动态规划是一种把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。常用于有重叠子问题和最优子结构性质的问题。

其思想大致上是：对于一个给定问题，解其子问题，再合并子问题的解，最终得出原问题的解。

而许多子问题非常相似，为此动态规划算法试图仅仅解决每个子问题一次，从而减少计算量。并且，储存每个解出的子问题的解，以便查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

性质

最优子结构性质：最优解所包含的子问题的解也是最优的。

子问题重叠性质：在用递归算法自顶向下求解时候，每次产生的子问题并不总是新问题。所以对每个子问题只计算一次，并将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只需要查表即可。

无后效性：已经确定的状态不会改变。

滚动数组

描述

滚动数组是在使用动态规划算法中为了降低空间复杂度而使用的一种编程思想。每次使用固定的若干个储存空间，由于其储存元素在DP数组中对应的位置是变化的，就像是让数组滚动起来。

利用滚动数组可以在N很大的情况下压缩存储空间，降低时间复杂度。

※ 滚动数组适用于只对结果进行输出的情况，因为其没有对DP数组所有元素进行存储。

一维滚动数组

描述

可将空间复杂度降低为O(1)，也就是使用常数个变量对DP数组进行存储。

例子

$$DP[i]=DP[i-1]+DP[i-2]$$

就可以建立变量pre1和pre2对DP[i-1]和DP[i-2]进行存储（并实时更新）。

二维滚动数组

描述

实际上是将空间压缩到一行（列）上，使得空间复杂度为O(N)（N为列的数量）

例子

$$\begin{gathered} DP[0][0]=1 \\ DP[i][j]=DP[i-1][j]+DP[i][j-1] \end{gathered}$$

常规动态规划做法如下

for(int i=0;i<=n;i++){
    for(int j=0;j<=m;j++){
        if(i>0){
            dp[i][j]+=dp[i-1][j];
        }
        if(j>0){
            dp[i][j]+=dp[i][j-1];
        }
    }
}

利用滚动数组的动态规划做法如下（只需要用到一维DP数组）,有效地降低了空间复杂度

for(int i=0;i<=n;i++){
    for(int j=0;j<=m;j++){
        if(j>0){
            dp[j]+=dp[j-1];
        }
    }
}

组）,有效地降低了空间复杂度

for(int i=0;i<=n;i++){
    for(int j=0;j<=m;j++){
        if(j>0){
            dp[j]+=dp[j-1];
        }
    }
}