【数据结构与算法】data structures & algorithms 第七章：散列表算法的初步运用

数据结构与算法系列文章目录

【数据结构与算法】data structures & algorithms 第一章：复杂度分析
【数据结构与算法】data structures & algorithms 第二章：基本概念
【数据结构与算法】data structures & algorithms 第三章：线性数据结构
【数据结构与算法】data structures & algorithms 第四章：树的数据结构
【数据结构与算法】data structures & algorithms 第五章：图的数据结构
【数据结构与算法】data structures & algorithms 第六章：各类常见的排序算法
【数据结构与算法】data structures & algorithms 第七章：散列表算法的初步运用
【数据结构与算法】data structures & algorithms 第八章：红黑树的理解与使用

---

---

一、散列表简介

• 已知的几种查找方法：

  • 顺序查找，$O(N)$；
  • 二分查找（静态查找），$O(\log N)$；
  • 二叉搜索树，$O(h)$ h为二叉查找树的高度
  • 平衡二叉树，$O(\log N)$；

• 如何快速搜索到需要的关键词，如果关键词不方便比较怎么办

  • 查找的本质：已知对象找位置
    • 有序安排对象：全序、半序；
    • 直接”算出“对象位置：散列
  • 散列查找法的两项基本工作：
    • 计算位置：构造散列函数确定关键词存储位置；
    • 解决冲突：应用某种策略解决多个关键词位置相同的问题；
  • 时间复杂度几乎是常量：$O(1)$，即查找时间与问题规模无关；

• 散列表（哈希表）

  • 类型名称：符号表$(SymbolTable)$
  • 数据对象集：符号表是”名字$(Name)$-属性$(Attribute)$“对的集合
  • 操作集：$Table\in SymbolTable,Name\in NameType,Attr\in AttributeType$
    • $SymbolTableInitializeTable(intTableSize)$：
      创建一个长度为$TableSize$的符号表；
    • $BooleanIsIn(SymbolTableTable,NameTypeName)$：
      查找特定的名字$Name$是否在符号表$Table$中；
    • $AttributeTypeFind(SymbolTableTable,NameTypeName)$：
      获取$Table$中指定名字$Name$对应的属性；
    • $SymbolTableModefy(SymbolTableTable,NameTypeName,AttributeTypeAttr)$：
      将$Table$中指定名字$Name$的属性修改为$Attr$；
    • $SymbolTableInsert(SymbolTableTable,NameTypeName,AttributeTypeAttr)$：
      向$Table$中插入一个新名字$Name$及其属性$Attr$；
    • $SymbolTableDelete(SymbolTableTable,NameTypeName)$：
      从$Table$中删除一个名字$Name$及其属性；

• 散列的基本思想：

  • 以关键字key为自变量，通过一个确定的函数h （散列函数），计算处对应的函数值h(key)，作为数据对象的存储地址；
  • 可能不同的关键字会映射到同一个散列地址上，即$h(ke{y}_i)=h(ke{y}_j)，当ke{y}_i\ne ke{y}_j$，称为冲突（Collison）；–需要某种冲突解决策略

• 装填因子（Loading Factor）：设散列表空间大小为m，填入表中元素个数是n，则称$\alpha =n/m$为散列表的装填因子；

• 如果没有冲突溢出：
  $T_{查询}=T_{插入}=T_{删除}=O(1)$；

二、散列函数的构造方法

• 散列函数应该考虑两个因素：

  • 计算简单，以便提高转换速度；
  • 关键字对应的地址空间分布均匀，以尽量减少冲突；

• 数字关键字的散列函数构造

  • 1、直接定址法
    取关键词的某个线性函数值为散列地址，即$h(key)=a\times key+b$，a、b为常数；
    如 $h(key)=key-1990$：
    

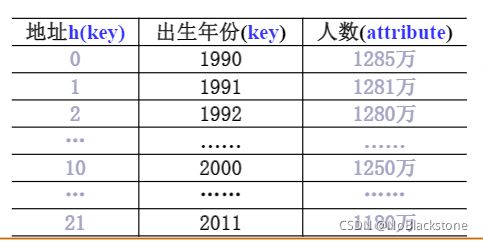
  • 2、除留余数法
    散列函数为：$h(key)=keymodp$；一般地，p 取素数
    如 $h(key)=key\%17$
    

  • 3、数学分析法
    分析数字关键字在各位上的变化情况，取比较随机的位作为散列地址；
    如：取11位手机号码key的后4位作为地址：散列函数为：
    $h(key)=atoi(key+7)$
    如果关键字key是18位的身份证号码：
    

  • 4、折叠法
    把关键字分割成位数相同的几个部分，然后折叠
    

  • 5、平方取中法
    

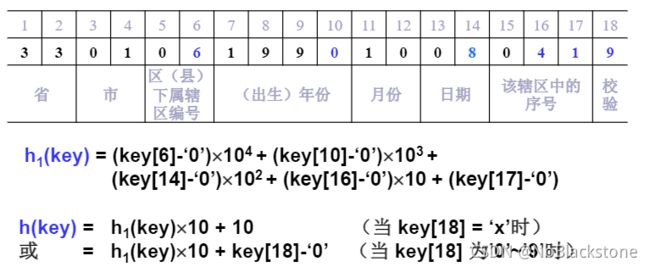
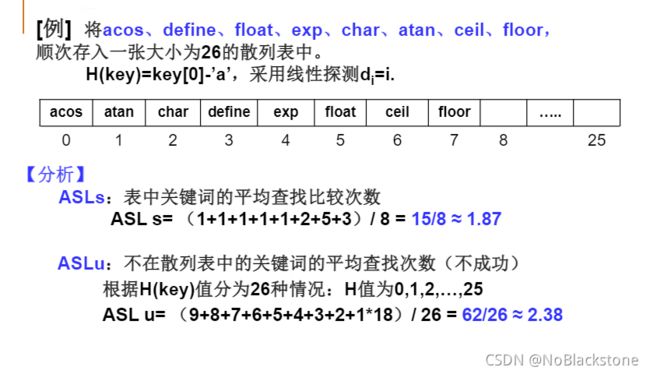
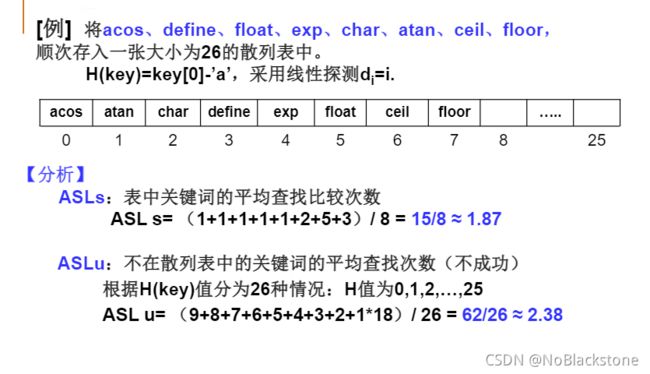
• 字符关键词的散列函数构造

  • 1、一个简单的散列函数——ASCII码和法
    对字符型关键词key定义散列函数如下：
    $h(key)=(\sum key[i])modTableSize$；存在冲突：a3、b2、c1；eat、tea；
  • 2、简单的改进——前3个字符移位法
    $h(key)=(key[0]\times 27^2+key[1]\times 27+key[2])modTableSize$；存在冲突：string、street、strong、structure等等；空间浪费：$3000/26^3\approx 30\%$；
  • 3、好的散列函数——移位法
    涉及关键词所有n个字符，并且分布得很好：
    $h(key)=({\sum }_{i=0}^{n-1}key[n-i-1]\times 32^i)modTableSize$；

• 针对移位法做到快速计算：
  $h("abcde"){=}^{\prime }{a}^{\prime }\ast 32^4{+}^{\prime }{b}^{\prime }\ast 32^3{+}^{\prime }{c}^{\prime }\ast 32^2{+}^{\prime }{d}^{\prime }\ast 32{+}^{\prime }{e}^{\prime }$，做到形如$(((a\times 32+b)\times 32+c)\times 32+d)\times 32+e$；

一、散列表简介

• 已知的几种查找方法：

  • 顺序查找，$O(N)$；
  • 二分查找（静态查找），$O(\log N)$；
  • 二叉搜索树，$O(h)$ h为二叉查找树的高度
  • 平衡二叉树，$O(\log N)$；

• 如何快速搜索到需要的关键词，如果关键词不方便比较怎么办

  • 查找的本质：已知对象找位置
    • 有序安排对象：全序、半序；
    • 直接”算出“对象位置：散列
  • 散列查找法的两项基本工作：
    • 计算位置：构造散列函数确定关键词存储位置；
    • 解决冲突：应用某种策略解决多个关键词位置相同的问题；
  • 时间复杂度几乎是常量：$O(1)$，即查找时间与问题规模无关；

• 散列表（哈希表）

  • 类型名称：符号表$(SymbolTable)$
  • 数据对象集：符号表是”名字$(Name)$-属性$(Attribute)$“对的集合
  • 操作集：$Table\in SymbolTable,Name\in NameType,Attr\in AttributeType$
    • $SymbolTableInitializeTable(intTableSize)$：
      创建一个长度为$TableSize$的符号表；
    • $BooleanIsIn(SymbolTableTable,NameTypeName)$：
      查找特定的名字$Name$是否在符号表$Table$中；
    • $AttributeTypeFind(SymbolTableTable,NameTypeName)$：
      获取$Table$中指定名字$Name$对应的属性；
    • $SymbolTableModefy(SymbolTableTable,NameTypeName,AttributeTypeAttr)$：
      将$Table$中指定名字$Name$的属性修改为$Attr$；
    • $SymbolTableInsert(SymbolTableTable,NameTypeName,AttributeTypeAttr)$：
      向$Table$中插入一个新名字$Name$及其属性$Attr$；
    • $SymbolTableDelete(SymbolTableTable,NameTypeName)$：
      从$Table$中删除一个名字$Name$及其属性；

• 散列的基本思想：

  • 以关键字key为自变量，通过一个确定的函数h**（散列函数），计算处对应的函数值h(key)**，作为数据对象的存储地址；
  • 可能不同的关键字会映射到同一个散列地址上，即$h(ke{y}_i)=h(ke{y}_j)，当ke{y}_i\ne ke{y}_j$，称为冲突（Collison）；–需要某种冲突解决策略

• 装填因子（Loading Factor）：设散列表空间大小为m，填入表中元素个数是n，则称$\alpha =n/m$为散列表的装填因子；

• 如果没有冲突溢出：
  $T_{查询}=T_{插入}=T_{删除}=O(1)$；

二、散列函数的构造方法

• 散列函数应该考虑两个因素：

  • 计算简单，以便提高转换速度；
  • 关键字对应的地址空间分布均匀，以尽量减少冲突；

• 数字关键字的散列函数构造

  • 1、直接定址法
    取关键词的某个线性函数值为散列地址，即$h(key)=a\times key+b$，a、b为常数；
    如 $h(key)=key-1990$：
    [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EWvVgPkg-1635140077820)(picture\80.png)]

  • 2、除留余数法
    散列函数为：$h(key)=keymodp$；一般地，p 取素数
    如 $h(key)=key\%17$
    [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PGhetn5A-1635140077821)(picture\81.png)]

  • 3、数学分析法
    分析数字关键字在各位上的变化情况，取比较随机的位作为散列地址；
    如：取11位手机号码key的后4位作为地址：散列函数为：
    $h(key)=atoi(key+7)$
    如果关键字key是18位的身份证号码：
    [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uUlgSvoK-1635140077822)(picture\82.png)]

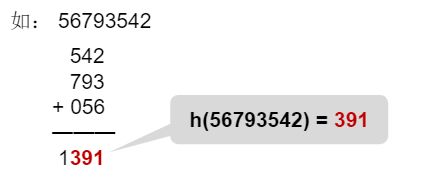
  • 4、折叠法
    把关键字分割成位数相同的几个部分，然后折叠
    [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bww1ECEB-1635140077823)(picture\83.PNG)]

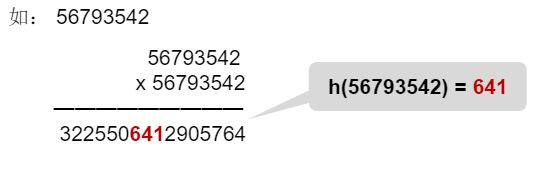
  • 5、平方取中法
    [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mdEuJfAs-1635140077824)(picture\84.png)]

• 字符关键词的散列函数构造

  • 1、一个简单的散列函数——ASCII码和法
    对字符型关键词key定义散列函数如下：
    $h(key)=(\sum key[i])modTableSize$；存在冲突：a3、b2、c1；eat、tea；
  • 2、简单的改进——前3个字符移位法
    $h(key)=(key[0]\times 27^2+key[1]\times 27+key[2])modTableSize$；存在冲突：string、street、strong、structure等等；空间浪费：$3000/26^3\approx 30\%$；
  • 3、好的散列函数——移位法
    涉及关键词所有n个字符，并且分布得很好：
    $h(key)=({\sum }_{i=0}^{n-1}key[n-i-1]\times 32^i)modTableSize$；

• 针对移位法做到快速计算：
  $h("abcde"){=}^{\prime }{a}^{\prime }\ast 32^4{+}^{\prime }{b}^{\prime }\ast 32^3{+}^{\prime }{c}^{\prime }\ast 32^2{+}^{\prime }{d}^{\prime }\ast 32{+}^{\prime }{e}^{\prime }$，做到形如$(((a\times 32+b)\times 32+c)\times 32+d)\times 32+e$；

Index Hash(const char *Key, int TableSize) {
   unsigned int h = 0;  //散列函数值，初始化为0
   while (*Key != '\0')  //位移映射
       h = (h << 5) + *Key++;
   return h % TableSize;
}

三、冲突处理方法

• 常用处理冲突的思路：
  • 换个位置：开放地址法；
  • 同一位置的冲突对象组织在一起：链地址法；

1、开放地址法

• 一旦产生了冲突（该地址已有其它元素），就按某种规则去寻找另一空地址；
• 若发生了第i次冲突，试探地下一个地址将增加d_i，基本公式是：
  $h_i(key)=(h(key)+d_i)modTableSiz(1\le i<TableSzie)$；
• **d_i**决定了不同的解决冲突方案：线性探测$d_i=i$、平方探测$d_i=\pm i^2$、双散列$d_i=i\ast h_2(key)$；

1.1、线性探测法（Linear Probing）

• 线性探测法：以**增量序列 1，2，…，(TableSize - 1)**循环试探下一个存储地址；

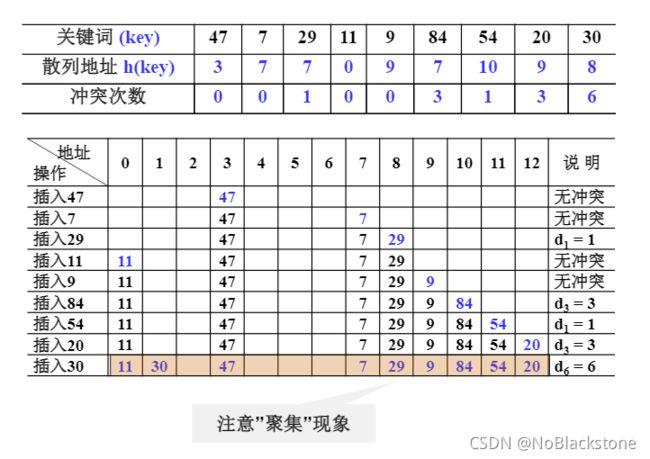
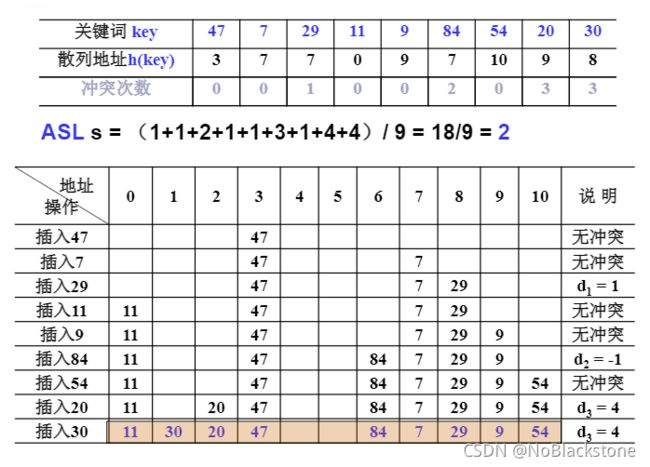
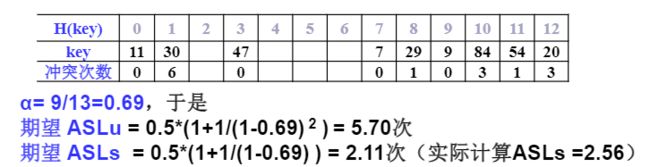
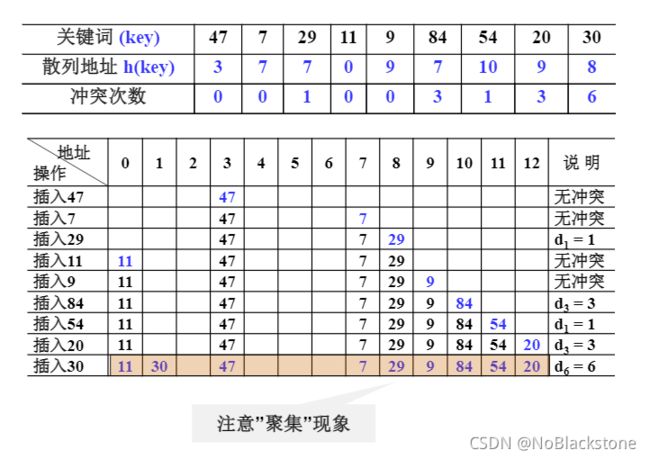
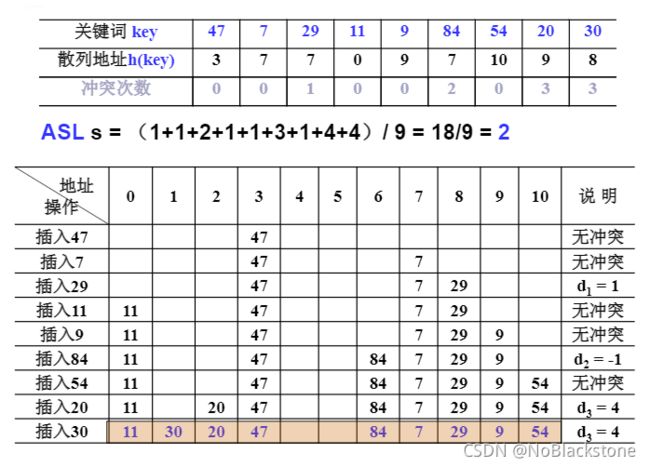
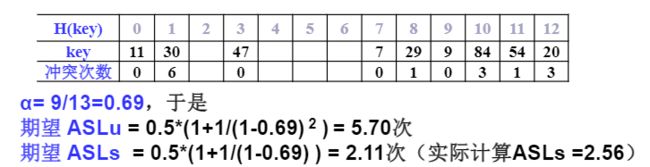
• 例子设关键词序列为 $\{47,7,29,11,9,84,54,20,30\}$，

  • 散列表表长TableSize = 13（装填因子 $\alpha =9/13\approx 0.69$）；
  • 散列函数为：$h(key)=keymod11$；

  用线性探测法处理冲突，列出依次插入后的散列表，并估算查找性能；

• 线性探测法处理冲突，容易出现聚集现象；

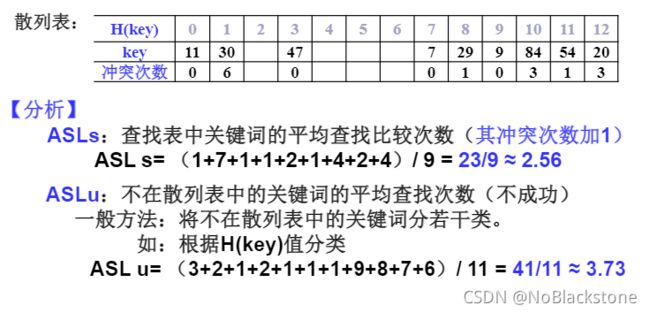
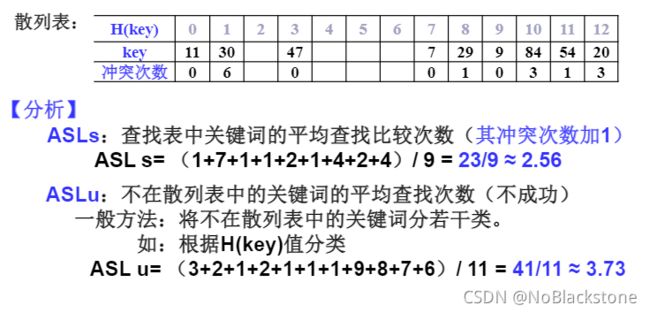
• 散列表查找性能分析2

  • 成功平均查找长度 （ASLs）
  • 不成功平均查找长度 （ASLu）

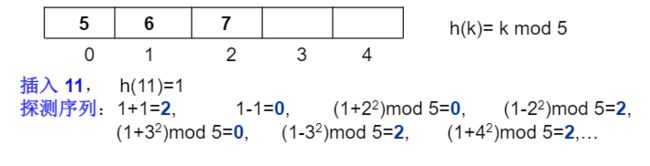
1.2、平方探测法（Quadratic Probing）—二次探测

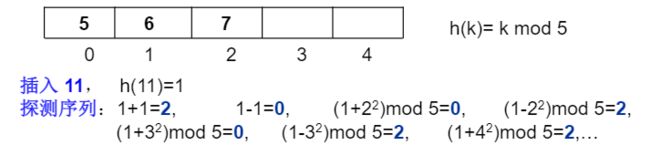
• 平方探测法：以增量序列 $1^2,-1^2,2^2,-2^2,\cdots ,q^2,-q^2$ 且 $q\le \lfloor TableSize/2\rfloor$循环试探下一个存储地址；

• 如果散列表长度TableSize 是某个 4k + 3（k是正整数）形式的素数时，平方探测法就可以探查到整个散列表空间；
• 不然容易在几个地址上来回探测，如下图：

struct HashTbl{
    int TableSize;
    Cell *TheCells;
};
using HashTable = *HashTbl;

HashTable initializeTable (int TableSize) {
    if (TableSize < minTableSize) {
        Error ("散列表太小");
        return NULL;
    }
    
    HashTable H = new HashTable;
    if (H == NULL) {
        FatalError ("空间溢出");
    }
    
    H->TableSize = NextPrime(TableSize);  //调整为素数大小的散列表；
    
    //分配散列表Cells
    H->TheCells = new Cell[H->TableSize];
    if (H->TheCells == NULL) {
        FatalError ("空间溢出");
    }
    
    for (int i = 0; i < H->TableSize; ++i) {
        H->TheCells[i].Info = Empty;  //数组设计为结构数组形式
    }
    return H;
}

• 结构数组形式：

Position Find (elementType key, HashTable H) {
    Position currentPos, newPos; 
    int CNum = 0;  //记录冲突次数
    
    newPos = currentPos = Hash (key, H->TableSize); //返回一个地址
    while (H->TheCells[newPos].Info != Empty && H->TheCells[newPos].Element != key) {
        //字符串类型的关键词需要strcmp函数
        //判断冲突的奇偶次数
        if (++CNum % 2) {
            newPos = currentPos + (CNum + 1) / 2 * (CNum + 1) / 2;
            while (newPos >= H->TableSize) {
                newPos -= H->TableSize;
            }
        }
        else {
            newPos = currentPos - CNum / 2 * CNum / 2;
            while (newPos < 0) {
                newPos += H->TableSize;
            }
        }
    }
    return newPos;
}

void Insert (elementType key, HashTable H) {
    Position Pos = Find (key, H);
    if (H->TheCells[Pos].Info != Legitimate) {
        H->TheCells[Pos].Info = Legitimate;
        H->TheCells[Pos].Element = key;
        //字符串类型的关键词需要strcpy函数
    }
}

• 在开放地址法的散列表中，删除操作要很小心；
  通常只能懒惰删除，即需要增加一个删除标志（Deleted），而并不是真正删除它；
  以便查找时不会断链，其空间可以在下次插入时重用；

1.3、双散列探测法（Double Hashing）

• 双散列探测法：d_i为i * h₂(key)，h₂(key)是另一个散列函数
  探测序列成：h₂*(key), 2h₂(key), 3h₂(key), …
• 对任意的key，$h_2(key)\ne 0$；
• 探测序列还应该保证所有的散列存储单元都应该能够被探测到；选择以下形式有良好的效果：
  $h_2(key)=p-(keymodp)$，其中：$p<TableSize,p、TableSize都是素数$；

1.4、再散列（Rehashing）

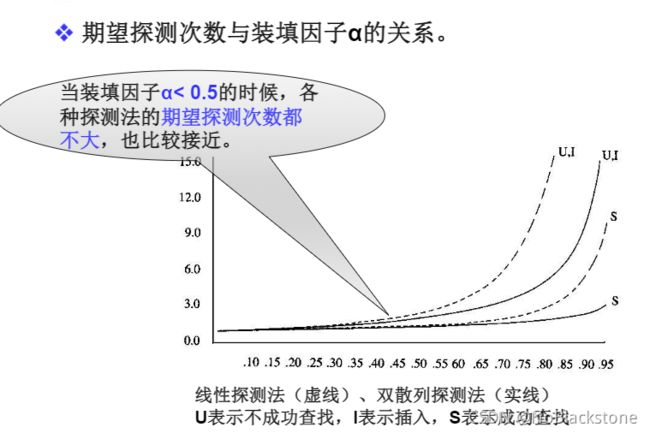
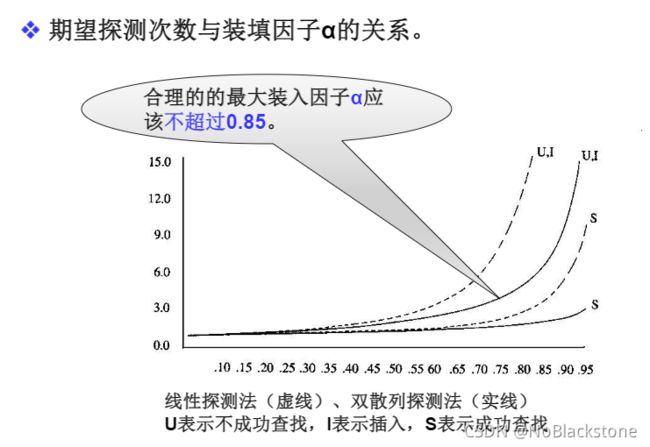
• 当散列表元素太多（即装填因子$\alpha$太大）时，查找效率会下降；
  • 实用最大装填因子一般取$0.5\le \alpha \le 0.85$；
• 当装填因子过大时，解决的方法是加倍扩大散列表，这个过程叫做再散列；

2、链地址法

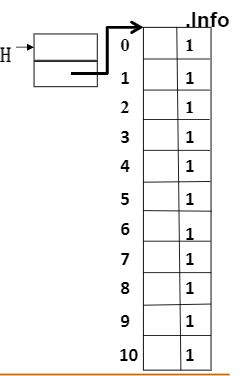
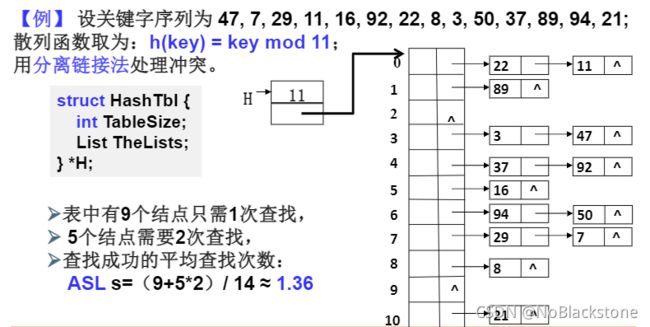
2.1、分离链接法（Separate Chaining）

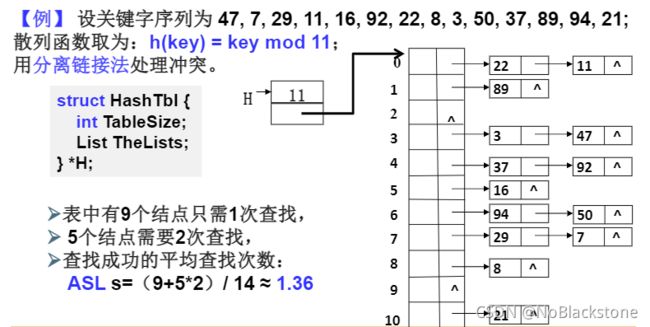
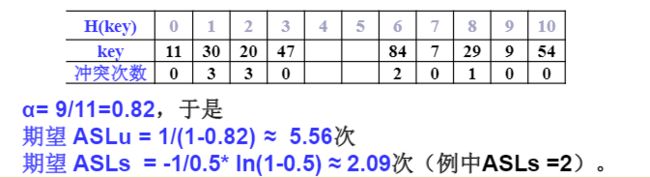
• 分离链接法：将相应位置上冲突的所有关键词存储在同一个单链表中；

• 例子

struct ListNode {
    elementType Element;
    ListNode *Next;
};
using Position = *ListNode;,
using List = *ListNode;

struct HashTbl {
    int TableSize;
    List TheLists;
};
using HashTable = *HashTbl;

Position Find (elementType key, HashTable H) {
    int Pos = Hash(key, H->TableSize);  //初始散列位置
    Position P = H->TheLists[Pos].Next;  //获得链表头
    while (P != NULL && strcmp(P->Element, key)) {
        P = P->Next;
    }
    return P;
}

四、散列表的性能分析

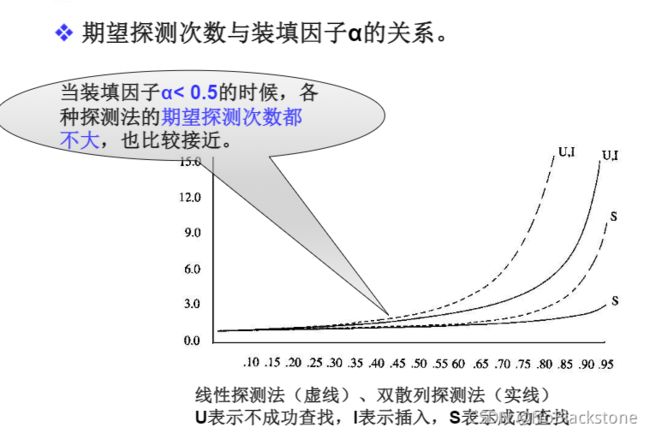
• 平均查找长度（ASL）用来度量散列表查找效率：成功、不成功；
• 关键词的比较次数，取决于产生冲突的多少，影响产生冲突多少有以下三个因素：
  • 散列函数是否均匀；
  • 处理冲突的方法；
  • 散列表的装填因子$\alpha$；

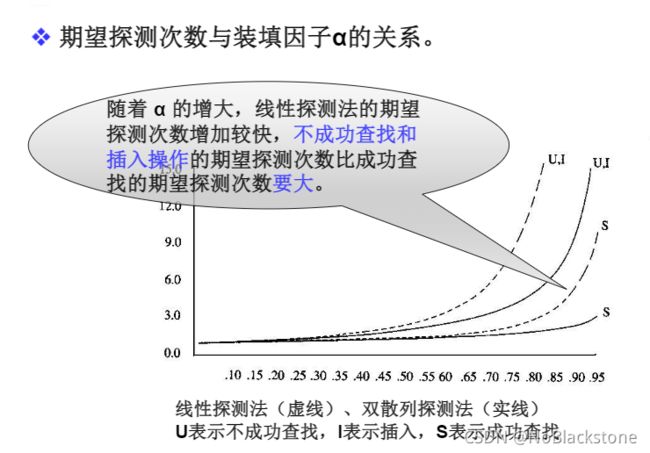
1、线性探测法的查找性能

• 线性探测法的期望探测次数 满足下列公式：
  $p=\{\begin{array}{ll}\frac{1}{2}[1+\frac{1}{{(1-\alpha )}^2}]& (对插入和不成功查找而言)\\ \frac{1}{2}(1+\frac{1}{1-\alpha })& (对成功查找而言)\end{array}$
• 当 $\alpha =0.5$时，
  • 插入操作和不成功查找的期望 $ASLu=0.5\ast (1+1/{(1-0.5)}^2)=2.5$ 次；
  • 成功查找的期望 $ASLs=0.5\ast (1+1/(1-0.5))=1.5$ 次；

2、平方探测法和双散列探测法的查找性能

• 平方探测法和双散列探测法的探测次数 满足下列公式：
  $p=\{\begin{array}{ll}\frac{1}{1-\alpha }& (对插入和不成功查找而言)\\ -\frac{1}{\alpha }\ln (1-\alpha )& (对成功查找而言)\end{array}$
• 当 $\alpha =0.5$ 时，
  • 插入操作和不成功查找的期望 $ASLu=1/(1-0.5)=2$ 次；
  • 成功查找的期望 $ASLs=-1/0.5\ast \ln (1-0.5)\approx 1.39$ 次；

3、分离链接法的查找性能

• 所有地址链表的平均长度定义成装填因子 $\alpha$，$\alpha$有可能超过1；
• 其期望探测次数p为：
  $p=\{\begin{array}{ll}\alpha +e^{-\alpha }& (对插入和不成功查找而言)\\ 1+\frac{\alpha }{2}& (对成功查找而言)\end{array}$
• 当 $\alpha =1$ 时，
  • 插入操作和不成功查找的期望 $ASLu=1+e^{-1}=1.37$ 次；
  • 成功查找的期望 $ASLs=1+1/2=1.5$ 次；

4、总结

• 选择合适的 h(key)，散列法的查找效率期望是常数O(1)，它几乎与关键字的空间的大小n无关；也适合于关键字直接比较计算量大的问题；
• 它是以较小的 $\alpha$为前提；因此，散列方法是一个以空间换时间；
• 散列方法的存储对关键字是随机的，不便于顺序查找关键字，也不适合于范围查找，或最大值最小值查找；

4.1、开放地址法

• 散列表是一个数组，存储效率高，随机查找；
• 散列表有”聚集”现象；

4.2、分离链法

• 散列表是顺序存储和链式存储的结合，链表部分的存储效率和查找效率都比较低；
• 关键词删除不需要“懒惰删除”法，从而没有存储“垃圾”；
• 太小的$\alpha$可能导致空间浪费，大的$\alpha$又将付出更多的时间代价；
• 不均匀的链表长度导致时间效率的严重下降；

Index Hash(const char *Key, int TableSize) {
    unsigned int h = 0;  //散列函数值，初始化为0
    while (*Key != '\0')  //位移映射
        h = (h << 5) + *Key++;
    return h % TableSize;
}

三、冲突处理方法

• 常用处理冲突的思路：
  • 换个位置：开放地址法；
  • 同一位置的冲突对象组织在一起：链地址法；

1、开放地址法

• 一旦产生了冲突（该地址已有其它元素），就按某种规则去寻找另一空地址；
• 若发生了第i次冲突，试探地下一个地址将增加d_i，基本公式是：
  $h_i(key)=(h(key)+d_i)modTableSiz(1\le i<TableSzie)$；
• **d_i**决定了不同的解决冲突方案：线性探测$d_i=i$、平方探测$d_i=\pm i^2$、双散列$d_i=i\ast h_2(key)$；

1.1、线性探测法（Linear Probing）

• 线性探测法：以**增量序列 1，2，…，(TableSize - 1)**循环试探下一个存储地址；

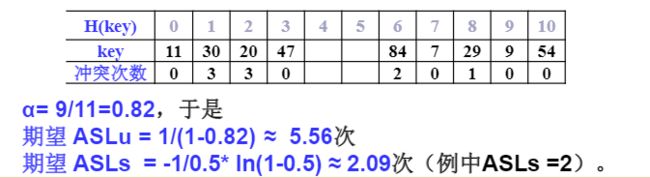
• 例子设关键词序列为 $\{47,7,29,11,9,84,54,20,30\}$，

  • 散列表表长TableSize = 13（装填因子 $\alpha =9/13\approx 0.69$）；
  • 散列函数为：$h(key)=keymod11$；

  用线性探测法处理冲突，列出依次插入后的散列表，并估算查找性能；

• 线性探测法处理冲突，容易出现聚集现象；

• 散列表查找性能分析2

  • 成功平均查找长度 （ASLs）
  • 不成功平均查找长度 （ASLu）

1.2、平方探测法（Quadratic Probing）—二次探测

• 平方探测法：以增量序列 $1^2,-1^2,2^2,-2^2,\cdots ,q^2,-q^2$ 且 $q\le \lfloor TableSize/2\rfloor$循环试探下一个存储地址；

• 如果散列表长度TableSize 是某个 4k + 3（k是正整数）形式的素数时，平方探测法就可以探查到整个散列表空间；
• 不然容易在几个地址上来回探测，如下图：

struct HashTbl{
    int TableSize;
    Cell *TheCells;
};
using HashTable = *HashTbl;

HashTable initializeTable (int TableSize) {
    if (TableSize < minTableSize) {
        Error ("散列表太小");
        return NULL;
    }
    
    HashTable H = new HashTable;
    if (H == NULL) {
        FatalError ("空间溢出");
    }
    
    H->TableSize = NextPrime(TableSize);  //调整为素数大小的散列表；
    
    //分配散列表Cells
    H->TheCells = new Cell[H->TableSize];
    if (H->TheCells == NULL) {
        FatalError ("空间溢出");
    }
    
    for (int i = 0; i < H->TableSize; ++i) {
        H->TheCells[i].Info = Empty;  //数组设计为结构数组形式
    }
    return H;
}

• 结构数组形式：

Position Find (elementType key, HashTable H) {
    Position currentPos, newPos; 
    int CNum = 0;  //记录冲突次数
    
    newPos = currentPos = Hash (key, H->TableSize); //返回一个地址
    while (H->TheCells[newPos].Info != Empty && H->TheCells[newPos].Element != key) {
        //字符串类型的关键词需要strcmp函数
        //判断冲突的奇偶次数
        if (++CNum % 2) {
            newPos = currentPos + (CNum + 1) / 2 * (CNum + 1) / 2;
            while (newPos >= H->TableSize) {
                newPos -= H->TableSize;
            }
        }
        else {
            newPos = currentPos - CNum / 2 * CNum / 2;
            while (newPos < 0) {
                newPos += H->TableSize;
            }
        }
    }
    return newPos;
}

void Insert (elementType key, HashTable H) {
    Position Pos = Find (key, H);
    if (H->TheCells[Pos].Info != Legitimate) {
        H->TheCells[Pos].Info = Legitimate;
        H->TheCells[Pos].Element = key;
        //字符串类型的关键词需要strcpy函数
    }
}

• 在开放地址法的散列表中，删除操作要很小心；
  通常只能懒惰删除，即需要增加一个删除标志（Deleted），而并不是真正删除它；
  以便查找时不会断链，其空间可以在下次插入时重用；

1.3、双散列探测法（Double Hashing）

• 双散列探测法：d_i为i * h₂(key)，h₂(key)是另一个散列函数
  探测序列成：h₂*(key), 2h₂(key), 3h₂(key), …
• 对任意的key，$h_2(key)\ne 0$；
• 探测序列还应该保证所有的散列存储单元都应该能够被探测到；选择以下形式有良好的效果：
  $h_2(key)=p-(keymodp)$，其中：$p<TableSize,p、TableSize都是素数$；

1.4、再散列（Rehashing）

• 当散列表元素太多（即装填因子$\alpha$太大）时，查找效率会下降；
  • 实用最大装填因子一般取$0.5\le \alpha \le 0.85$；
• 当装填因子过大时，解决的方法是加倍扩大散列表，这个过程叫做再散列；

2、链地址法

2.1、分离链接法（Separate Chaining）

• 分离链接法：将相应位置上冲突的所有关键词存储在同一个单链表中；

• 例子

struct ListNode {
    elementType Element;
    ListNode *Next;
};
using Position = *ListNode;,
using List = *ListNode;

struct HashTbl {
    int TableSize;
    List TheLists;
};
using HashTable = *HashTbl;

Position Find (elementType key, HashTable H) {
    int Pos = Hash(key, H->TableSize);  //初始散列位置
    Position P = H->TheLists[Pos].Next;  //获得链表头
    while (P != NULL && strcmp(P->Element, key)) {
        P = P->Next;
    }
    return P;
}

四、散列表的性能分析

• 平均查找长度（ASL）用来度量散列表查找效率：成功、不成功；
• 关键词的比较次数，取决于产生冲突的多少，影响产生冲突多少有以下三个因素：
  • 散列函数是否均匀；
  • 处理冲突的方法；
  • 散列表的装填因子$\alpha$；

1、线性探测法的查找性能

• 线性探测法的期望探测次数 满足下列公式：
  $p=\{\begin{array}{ll}\frac{1}{2}[1+\frac{1}{{(1-\alpha )}^2}]& (对插入和不成功查找而言)\\ \frac{1}{2}(1+\frac{1}{1-\alpha })& (对成功查找而言)\end{array}$
• 当 $\alpha =0.5$时，
  • 插入操作和不成功查找的期望 $ASLu=0.5\ast (1+1/{(1-0.5)}^2)=2.5$ 次；
  • 成功查找的期望 $ASLs=0.5\ast (1+1/(1-0.5))=1.5$ 次；

2、平方探测法和双散列探测法的查找性能

• 平方探测法和双散列探测法的探测次数 满足下列公式：
  $p=\{\begin{array}{ll}\frac{1}{1-\alpha }& (对插入和不成功查找而言)\\ -\frac{1}{\alpha }\ln (1-\alpha )& (对成功查找而言)\end{array}$
• 当 $\alpha =0.5$ 时，
  • 插入操作和不成功查找的期望 $ASLu=1/(1-0.5)=2$ 次；
  • 成功查找的期望 $ASLs=-1/0.5\ast \ln (1-0.5)\approx 1.39$ 次；

3、分离链接法的查找性能

• 所有地址链表的平均长度定义成装填因子 $\alpha$，$\alpha$有可能超过1；
• 其期望探测次数p为：
  $p=\{\begin{array}{ll}\alpha +e^{-\alpha }& (对插入和不成功查找而言)\\ 1+\frac{\alpha }{2}& (对成功查找而言)\end{array}$
• 当 $\alpha =1$ 时，
  • 插入操作和不成功查找的期望 $ASLu=1+e^{-1}=1.37$ 次；
  • 成功查找的期望 $ASLs=1+1/2=1.5$ 次；

4、总结

• 选择合适的 h(key)，散列法的查找效率期望是常数O(1)，它几乎与关键字的空间的大小n无关；也适合于关键字直接比较计算量大的问题；
• 它是以较小的 $\alpha$为前提；因此，散列方法是一个以空间换时间；
• 散列方法的存储对关键字是随机的，不便于顺序查找关键字，也不适合于范围查找，或最大值最小值查找；

4.1、开放地址法

• 散列表是一个数组，存储效率高，随机查找；
• 散列表有”聚集”现象；

4.2、分离链法

• 散列表是顺序存储和链式存储的结合，链表部分的存储效率和查找效率都比较低；
• 关键词删除不需要“懒惰删除”法，从而没有存储“垃圾”；
• 太小的$\alpha$可能导致空间浪费，大的$\alpha$又将付出更多的时间代价；
• 不均匀的链表长度导致时间效率的严重下降；