LeetCode 热题 HOT 100 Java 题解 -- Part 1
练习地址
LeetCode 热题 HOT 100 Java 题解 -- Part 1
-
- 1. 两数之和 1
- 2. 两数相加 2
- 3. 无重复字符的最长子串 3
- 4. 寻找两个正序数组的中位数 4
- 5. 最长回文子串 5
- 6. 正则表达式匹配 10
- 7. 盛最多水的容器 11
- 8. 三数之和 15
- 9. 电话号码的字母组合 17
- 10. 删除链表的倒数第 N 个结点 19
- 11. 有效的括号 20
- 12. 合并两个有序链表 21
- 13. 括号生成 22
- 14. 合并K个升序链表 23
- 15. 下一个排列 31
- 16. 最长有效括号 32
- 17. 搜索旋转排序数组 33
- 18. 在排序数组中查找元素的第一个和最后一个位置
- 19. 组合总和 39
- 20. 接雨水 42
- 21. 全排列 46
- 22. 旋转图像 48
- 23. 字母异位词分组 49
- 24 最大子数组和 53
- 25. 跳跃游戏 55
- 26. 合并区间 56
- 27. 不同路径 62
- 28. 最小路径和 64
- 29. 爬楼梯 70
- 30. 编辑距离 72
- 31. 颜色分类 75
- 32. 最小覆盖子串 76
- 33. 子集 78
- 34. 单词搜索 79
- 35. 柱状图中最大的矩形 84
- 36. 最大矩形 85
1. 两数之和 1
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
解析
使用 Hash 表记录所有已遍历元素及对应的下标,遍历的同时查找满足条件的数字是否已遍历,若找到返回即可。
代码
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer,Integer> map = new HashMap<>();
int[] res = new int[0];
for(int i = 0; i < nums.length; i++){
if(map.containsKey(target - nums[i])) return new int[]{i, map.get(target - nums[i])};
map.put(nums[i],i);
}
return res;
}
}
2. 两数相加 2
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:

输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
解析
按位模拟加法,注意循环条件不要忘记进位。
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int cur = 0;
int carry = 0;//进位
ListNode dummy = new ListNode();
ListNode helper = dummy;
while(l1 != null || l2 != null || carry != 0){
int v1 = l1 == null ? 0 : l1.val;
int v2 = l2 == null ? 0 : l2.val;
int sum = v1 + v2 + carry;
cur = sum % 10;
carry = sum / 10;
helper.next = new ListNode(cur);
helper = helper.next;
if(l1 != null) l1 = l1.next;
if(l2 != null) l2 = l2.next;
}
return dummy.next;
}
}
3. 无重复字符的最长子串 3
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
解析
使用一个数组记录每个字符出现次数,在遍历的同时移动窗口左边界,最后返回窗口长度的最大值即可。
注:子串是连续的,子序列是不连续的
代码
class Solution {
public int lengthOfLongestSubstring(String s) {
int[] map = new int[128];
int res = 0;
// i : 窗口右边界 j : 窗口左边界
for(int i = 0 , j = 0;i < s.length(); i++){
map[s.charAt(i)]++;
while(map[s.charAt(i)] > 1){ //重复
map[s.charAt(j++)]--;//窗口左移
}
res = Math.max(res, i - j + 1);// i - j + 1是窗口的长度
}
return res;
}
}
4. 寻找两个正序数组的中位数 4
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
解析
本题可以抽象为:给定两个数组 A、B,如何找到从小到大排列的第 K 个数字,而中位数存在 K = K -1的下标映射关系
代码
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n = nums1.length + nums2.length;
if(n % 2 == 0){
return (findKth(nums1, 0, nums2, 0, n / 2) + findKth(nums1, 0, nums2, 0, n / 2 + 1)) / 2.0;
}else{
return findKth(nums1, 0, nums2, 0, n / 2 + 1);
}
}
//i: nums1的起始位置 j: nums2的起始位置
public int findKth(int[] nums1, int i, int[] nums2, int j, int k){
if( i >= nums1.length) return nums2[j + k - 1];//nums1为空数组
if( j >= nums2.length) return nums1[i + k - 1];//nums2为空数组
if(k == 1){
return Math.min(nums1[i], nums2[j]);
}
int midVal1 = (i + k / 2 - 1 < nums1.length) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
int midVal2 = (j + k / 2 - 1 < nums2.length) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
if(midVal1 < midVal2){
return findKth(nums1, i + k / 2, nums2, j , k - k / 2);
}else{
return findKth(nums1, i, nums2, j + k / 2 , k - k / 2);
}
}
}
5. 最长回文子串 5
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = “babad”
输出:“bab”
解释:“aba” 同样是符合题意的答案。
示例 2:
输入:s = “cbbd”
输出:“bb”
解析
中心扩展法,枚举回文子串的中心位置,每次循环需要分奇数和偶数两种情况。
题解
class Solution {
public String longestPalindrome(String s) {
int l = 0;
int r = 0;
int maxLen = 0;
for(int i = 0; i < s.length(); i++){
int len = Math.max(center(s, i, i), center(s, i, i + 1));
if(len > maxLen){
l = i - (len - 1) / 2;
r = i + len / 2;
maxLen = len;
}
}
return s.substring(l, r + 1);
}
//中心扩散法
private int center(String s, int left, int right){
while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){
left--;
right++;
}
return right - left - 1;
}
}
6. 正则表达式匹配 10
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = “a*”
输出:true
解释:因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:s = “ab”, p = “."
输出:true
解释:".” 表示可匹配零个或多个(‘*’)任意字符(‘.’)。
解析
使用动态规划来记录前面的匹配信息,
1、状态表示
f[i][j] 表示 s的前i个字符与 p中的前j个字符是否能够匹配
2、状态计算
p [ j ] ≠ ∗ ⟶ f ( i , j ) = f ( i − 1 , j − 1 ) & & match ( i , j ) p[j] \neq * \longrightarrow f(i, j)=f(i-1, j-1) \& \& \operatorname{match}(i, j) p[j]=∗⟶f(i,j)=f(i−1,j−1)&&match(i,j)
p [ j ] = ∗ ⟶ f ( i , j ) = f ( i , j − 2 ) ∥ f ( i − 1 , j − 2 ) & & match ( i , j − 1 ) ∥ f ( i − 2 , j − 2 ) & & match ( i − 1 , j − 1 ) & & match ( i , j − 1 ) ⋯ = f ( i , j − 2 ) ∥ f ( i − 1 , j ) & & match ( i , j − 1 ) p[j]=* \longrightarrow \\ f(i, j)=f(i, j-2)\|f(i-1, j-2) \& \& \operatorname{match}(i, j-1)\| f(i-2, j-2) \& \& \operatorname{match}(i-1, j-1) \& \& \operatorname{match}(i, j-1) \cdots \\ =f(i, j-2) \| f(i-1, j) \& \& \operatorname{match}(i, j-1) p[j]=∗⟶f(i,j)=f(i,j−2)∥f(i−1,j−2)&&match(i,j−1)∥f(i−2,j−2)&&match(i−1,j−1)&&match(i,j−1)⋯=f(i,j−2)∥f(i−1,j)&&match(i,j−1)
即
p [ j ] = ∗ ⟶ f ( i , j ) = f ( i , j − 2 ) ∥ f ( i − 1 , j ) & & match ( i , j − 1 ) p[j]=* \longrightarrow \\ f(i, j)=f(i, j-2)\|f(i-1, j) \& \& \operatorname{match}(i, j-1) p[j]=∗⟶f(i,j)=f(i,j−2)∥f(i−1,j)&&match(i,j−1)
其中match(i, j) 表示 s[i] 和 p[j] 匹配,即 s [ i ] = = p [ j ] ∣ p [ j ] = = " s[i] == p[j] | p[j] == " s[i]==p[j]∣p[j]=="
题解
class Solution {
public boolean isMatch(String s, String p) {
//f[i][j] 表示 s的前i个字符与 p中的前j个字符是否能够匹配
int n = s.length();
int m = p.length();
boolean[][] f = new boolean[n + 1][m + 1];
f[0][0] = true;
for(int i = 0; i < n + 1; i++){
for(int j = 1; j < m + 1; j++){
if(p.charAt(j - 1) != '*'){
f[i][j] = i >= 1 && j >= 1 && f[i - 1][j - 1] && match(s, p, i, j) ;
}else{
//* 匹配零个
boolean mathZero = j >= 2 && f[i][j - 2];
//* 匹配多个
boolean matchMany = i >= 1 && j >= 1 && f[i - 1][j] && match(s, p, i, j - 1);
f[i][j] = mathZero || matchMany;
}
}
}
return f[n][m];
}
private boolean match(String s, String p, int i, int j){
return s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.';
}
}
7. 盛最多水的容器 11
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
解析
使用首尾双指针,具体过程如下:
- 求出当前双指针对应的容器的容量;
- 由于对应数字较小的那个指针以后不可能作为容器的边界了,将其丢弃,并移动对应的指针。(移动短板)
代码
class Solution {
public int maxArea(int[] height) {
int ans = 0;
int l = 0;
int r = height.length - 1;
while(l < r){
//对应的容器的容量
int temp = (r - l) * Math.min(height[r], height[l]);
ans = Math.max(ans, temp);
//规则:移动短板
if(height[l] > height[r]){
r--;
}else{
l++;
}
}
return ans;
}
}
8. 三数之和 15
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
解析
先对数组排序,这样方便之后处理。整体思路为,通过遍历数组选取第一个数字,在遍历的同时用前后双指针寻
找满足条件的数字即可。
i去重,判断num[i] == num[i -1]
left去重:判断num[left] == num[left + 1]
right去重: 判断num[right] == num[right - 1]
题解
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
//排序方便去重
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<List<Integer>>();
for(int i = 0; i < nums.length; i++){
if(i > 0 && nums[i] == nums[i - 1]) continue; //i去重
int l = i + 1;
int r = nums.length - 1;
while(l < r){
int target = 0 - nums[i];
if(nums[l] + nums[r] == target){
List<Integer> list = new ArrayList<Integer>();
list.add(nums[i]);
list.add(nums[l]);
list.add(nums[r]);
res.add(list);
while(l < r && l + 1 < nums.length && nums[l] == nums[l + 1]) l++;//l去重
while(l < r && r - 1 >= 0 && nums[r] == nums[r - 1]) r--;//r去重
l++;
r--;
}else if(nums[l] + nums[r] < target){
l++;
}else{
r--;
}
}
}
return res;
}
}
9. 电话号码的字母组合 17
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
示例 2:
输入:digits = “”
输出:[]
示例 3:
输入:digits = “2”
输出:[“a”,“b”,“c”]
解析
首先存储每个数字对应的所有可能的字母,然后进行回溯操作。回溯过程中维护一个字符串,表示已有的字母排列,并记录当前回溯位置。每次尝试对应位置数字的所有字母,即可得到完整排列。
代码
class Solution {
List<String> res = new ArrayList<>();
StringBuilder sb = null;
String[] map = {"", "", "abc", "def",
"ghi", "jkl", "mno",
"pqrs", "tuv", "wxyz"};
public List<String> letterCombinations(String digits) {
if(digits == null || digits.length() == 0) return res;
sb = new StringBuilder();
dfs(digits, 0, sb);
return res;
}
private void dfs(String digits, int index, StringBuilder sb){
if(sb.length() == digits.length()){
res.add(new String(sb));
return;
}
String s = map[digits.charAt(index) - '0'];
for(int i = 0; i < s.length(); i++){
sb.append(s.charAt(i));
dfs(digits, index + 1, sb);
//回溯
sb.deleteCharAt(sb.length() - 1);
}
}
}
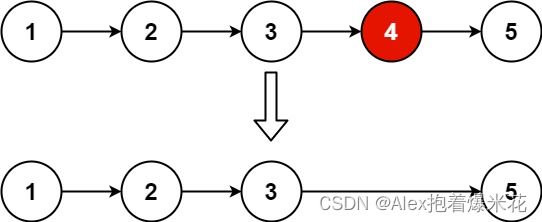
10. 删除链表的倒数第 N 个结点 19
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
解析
快慢双指针,令快指针先走 n 步,之后两指针再同步移动,直到快指针移动到链表结尾,此时慢指针指向的下一个位置即为要删除元素。
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode();
dummy.next = head;
ListNode fast = head;
for(int i = 0; i < n; i++){
fast = fast.next;
}
ListNode slow = dummy;
while(fast != null){
fast = fast.next;
slow = slow.next;
}
//走到了要删的前一个位置
slow.next = slow.next.next;
return dummy.next;
}
}
11. 有效的括号 20
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = “()”
输出:true
示例 2:
输入:s = “()[]{}”
输出:true
示例 3:
输入:s = “(]”
输出:false
解析
遍历字符串,每遇到一个左括号时,将与其匹配的右括号入栈;当遇到右括号时,与栈顶元素比较配对,不一致则匹配失败。
代码
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i = 0; i < s.length(); i++){
if(s.charAt(i) == '(') stack.push(')');
else if(s.charAt(i) == '[') stack.push(']');
else if(s.charAt(i) == '{') stack.push('}');
else if(stack.isEmpty() || stack.pop() != s.charAt(i)) return false;
}
return stack.isEmpty();
}
}
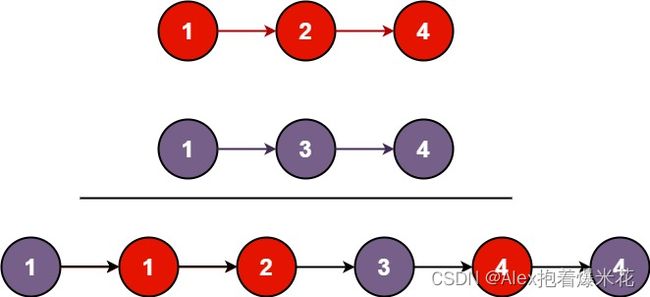
12. 合并两个有序链表 21
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
解析
同时遍历两个链表,从中选取较小的元素添加到结果链表,直至两个链表都遍历完成。归并排序的思想
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode dummy = new ListNode();
ListNode help = dummy;
while(list1 != null && list2 != null){
if(list1.val < list2.val){
help.next = list1;
list1 = list1.next;
}else{
help.next = list2;
list2 = list2.next;
}
help = help.next;
}
if(list1 != null) help.next = list1;
if(list2 != null) help.next = list2;
return dummy.next;
}
}
13. 括号生成 22
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]
示例 2:
输入:n = 1
输出:[“()”]
解析
一个合法的括号序列需要满足以下两个条件:
- 任意前缀中左括号的数量 ≥ 右括号的数量;
- 左右括号数量相等。
因此只要在回溯的同时,记录当前状态已使用的左右括号数,根据使用情况决定下一步状态即可。
代码
class Solution {
StringBuilder sb = null;
List<String> res = null;
public List<String> generateParenthesis(int n) {
sb = new StringBuilder();
res = new ArrayList<String>();
dfs(0, 0, n);
return res;
}
private void dfs(int left, int right, int n){
if(left == n && right == n){
res.add(new String(sb));
return;
}
if(left < n){
sb.append("(");
dfs(left + 1, right, n);
sb.deleteCharAt(sb.length() - 1);
}
if(right < n && right < left){
sb.append(")");
dfs(left, right + 1, n);
sb.deleteCharAt(sb.length() - 1);
}
}
}
14. 合并K个升序链表 23
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
解析
归并算法
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists == null || lists.length == 0) return null;
return merger(lists, 0, lists.length - 1);
}
private ListNode merger(ListNode[] lists, int l, int r){
if(l == r) return lists[l];
int mid = l + (r - l) / 2;
ListNode left = merger(lists, l, mid);
ListNode right = merger(lists, mid + 1, r);
return mergerTwoList(left, right);
}
private ListNode mergerTwoList(ListNode left, ListNode right){
if(left == null) return right;
if(right == null) return left;
ListNode dummy = new ListNode();
ListNode help = dummy;
while(left != null && right != null){
if(left.val < right.val){
help.next = left;
left = left.next;
}else{
help.next = right;
right = right.next;
}
help = help.next;
}
if(left != null) help.next = left;
if(right != null) help.next = right;
return dummy.next;
}
}
15. 下一个排列 31
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
解析
从后向前找到第一个升序数 k - 1;
从后向前找到第一个比 k - 1 大的数 t;
交换 k - 1和 t,并将原 k 位置后面的数字升序。
代码
class Solution {
public void nextPermutation(int[] nums) {
int k = nums.length - 1;
//从后往前找到第一个升序数 k - 1
while(k >= 1 && nums[k - 1] >= nums[k]) k--;
//没有升序全是降序
if(k == 0) Arrays.sort(nums);
else{
//从后往前找第一个大于k - 1的升序数
int t = nums.length - 1;
while(nums[t] <= nums[k - 1]) t--;
//交换,然后k之后的都是降序
int s = nums[t];
nums[t] = nums[k - 1];
nums[k - 1] = s;
//k之后的变为升序
Arrays.sort(nums, k, nums.length);
}
}
}
16. 最长有效括号 32
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = “(()”
输出:2
解释:最长有效括号子串是 “()”
示例 2:
输入:s = “)()())”
输出:4
解释:最长有效括号子串是 “()()”
示例 3:
输入:s = “”
输出:0
解析
一个合法的括号序列需要满足以下两个条件:
- 任意前缀中左括号的数量 ≥≥ 右括号的数量;
- 左右括号数量相等。
因此可以根据首次不合法的右括号(右括号数量首次大于左括号数量的位置)将原字符串划分成多段,可以看出,最长有效括号一定在段内产生;之后在每一段内找到所有合法括号序列,求出最大值即可。具体算法如下:
- 遇到左括号,将下标入栈;
- 遇到右括号:
- 如果栈不空,将栈顶元素出栈,与当前右括号匹配:
- 出栈后栈不空,则栈顶元素的下一个位置开始即为合法序列;
- 出栈后栈为空,则当前段起始点开始都为合法序列;
- 如果栈为空,说明此时右括号为首次不合法的右括号,更新段起始位置。
- 如果栈不空,将栈顶元素出栈,与当前右括号匹配:
代码
class Solution {
public int longestValidParentheses(String s) {
int res = 0;
int start = -1; //起始位置
Stack<Integer> stack = new Stack<>();
for(int i = 0; i < s.length(); i++){
if(s.charAt(i) == '('){
stack.push(i);//下标进栈
}else{
if(stack.isEmpty()){
start = i;//进去的是),更新起始位置
}else{
stack.pop();//弹出(
//栈为空和不为空,更新结果
if(!stack.isEmpty()){
res = Math.max(res, i - stack.peek());
}else{
res = Math.max(res, i - start);
}
}
}
}
return res;
}
}
17. 搜索旋转排序数组 33
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
解析
对于旋转数组,我们无法直接根据 nums[mid] 与 target 的大小关系来判断 target 是在 mid 的左边还是右边,因此需要「分段讨论」。
通过二分找到数组旋转点;
确定 target 在哪个区间;
子区间内二分查找。
代码
情况一
如果搜索区间[left, right]中一定有目标值索引,那么循环截止条件是while(left < right)
情况二
如果搜索区间[left, right]中不一定有目标值索引,那么循环截止条件是while(left <= right);(一般用于搜索区间内是否有某个值)
class Solution {
public int search(int[] nums, int target) {
int l = 0;
int r = nums.length - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target) return mid;
// l - mid 是有序数组, mid + 1 - r 是旋转数组(不有序)
if(nums[l] <= nums[mid]){
//判断是不是在l - mid有序数组中
if(target >= nums[l] && target < nums[mid]) r = mid - 1;
else l = mid + 1;
}else{
// l - mid 是旋转数组(不有序), mid + 1 - r 是有序数组
//判断是不是在mid + 1 - r有序数组中
if(target <= nums[r] && target > nums[mid]) l = mid + 1;
else r = mid - 1;
}
}
return -1;
}
}
18. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
解析
求左右边界的二分查找。
代码
拿[1,3,3,3,4],target = 3举例,第一次二分mid = 2,但是nums[2]的3并不是最左边界的3,然后leftOrRight为true,表示查找左侧边界的,所以要缩小右边界,right需要往左移,也就是right = mid-1,false 则相反,要查找右侧边界,即扩大左边界
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] res = new int[]{-1, -1};
res[0] = bsearch(nums, target, true);
res[1] = bsearch(nums, target, false);
return res;
}
private int bsearch(int[] nums, int target, boolean leftOrRight){
int res = -1;
int l = 0, r = nums.length - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(target > nums[mid]) l = mid + 1;
else if(target < nums[mid]) r = mid - 1;
else{
res = mid;
if(leftOrRight) r = mid - 1;
else l = mid + 1;
}
}
return res;
}
}
19. 组合总和 39
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
解析
依据每个位置的元素可选取的次数进行搜索。
代码
可以重复选择,所有 i = index, i 每次传递时不变
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> pre = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
dfs(candidates, target, 0);
return res;
}
private void dfs(int[] candidates, int target, int index) {
//等于零说明结果符合要求
if (target == 0) {
res.add(new ArrayList<>(pre));
return;
}
//遍历,index为本分支上一节点的减数的下标
for (int i = index; i < candidates.length; i++) {
//如果减数大于目标值,则差为负数,不符合结果
if (candidates[i] <= target) {
pre.add(candidates[i]);
//目标值减去元素值
dfs(candidates, target - candidates[i], i);
//每次回溯将最后一次加入的元素删除
pre.remove(pre.size() - 1);
}
}
}
}
20. 接雨水 42
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
解析
木桶原理,从当前节点往左找最高的高度,往右找最高的高度,这两个高度我们可以看做是木桶的两个木板,能接的雨水由最短的那块决定,累加每个位置能存的雨水量即可。
代码
class Solution {
public int trap(int[] height) {
int res = 0, l = 0, r = height.length - 1;
int lmax = 0, rmax = 0;
while(l < r){
//左右两侧最大高度
lmax = Math.max(lmax, height[l]);
rmax = Math.max(rmax, height[r]);
//移动短板
if(lmax <= rmax){
res = res + lmax - height[l];//短侧接雨水
l++;
}else{
res = res + rmax - height[r];
r--;
}
}
return res;
}
}
21. 全排列 46
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
解析
回溯法,维护两个数组,分别记录当前排列和每个数字的使用情况,之后枚举每个位置可能出现的数字即可。
代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> temp = new ArrayList<>();
boolean[] isused;
public List<List<Integer>> permute(int[] nums) {
isused = new boolean[nums.length];
dfs(nums, 0);
return res;
}
private void dfs(int[] nums, int index){
if(temp.size() == nums.length){
res.add(new ArrayList(temp));
}
for(int i = 0; i < nums.length; i++){
if(isused[i] == true) continue;
temp.add(nums[i]);
isused[i] = true;
dfs(nums, i + 1);
temp.remove(temp.size() - 1);
isused[i] = false;
}
}
}
22. 旋转图像 48
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
解析
通过两次翻转,完成顺时针旋转,分别是按主对角线翻转,然后再左右翻转即可。
代码
class Solution {
public void rotate(int[][] matrix) {
//对角线翻转
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < i; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i]= temp;
}
}
//左右对称翻转
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix.length / 2; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[i][matrix.length - j - 1];
matrix[i][matrix.length - j - 1]= temp;
}
}
}
}
23. 字母异位词分组 49
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
示例 1:
输入: strs = [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出: [[“bat”],[“nat”,“tan”],[“ate”,“eat”,“tea”]]
示例 2:
输入: strs = [“”]
输出: [[“”]]
示例 3:
输入: strs = [“a”]
输出: [[“a”]]
解析
将每个字符串排序后的结果作为 key,对原字符串数组进行分组,最后提取分组结果即可。
代码
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<>();
for(int i = 0; i < strs.length; i++){
//对字符串排序
char[] ch = strs[i].toCharArray();
Arrays.sort(ch);
String key = new String(ch);
//相同的字符串进行添加
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(strs[i]);
//放入map中
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}
}
24 最大子数组和 53
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
解析
前缀和(用于解决区间求和问题) + 动态规划
状态方程
f ( i ) = m a x ( f ( i − 1 ) + n u m s [ i ] , n u m s [ i ] ) f(i)=max(f(i−1)+nums[i],nums[i] ) f(i)=max(f(i−1)+nums[i],nums[i])
代码
class Solution {
public int maxSubArray(int[] nums) {
int res = nums[0], pre = nums[0];
for(int i = 1; i < nums.length; i++){
pre = Math.max(pre + nums[i], nums[i]);
res = Math.max(res, pre);
}
return res;
}
}
25. 跳跃游戏 55
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
解析
遍历数组的同时维护一个当时能跳到的最远位置,若不能到达此时下标,则说明不能到达最后一个下标,直接返回即可。
代码
class Solution {
public boolean canJump(int[] nums) {
int max = 0; // 能跳的最远距离
for(int i = 0; i < nums.length; i++){
if(i > max) return false;
max = Math.max(max, nums[i] + i);
}
return true;
}
}
26. 合并区间 56
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
解析
- 按照区间 左端点 排序;
- 设当前维护的区间端点为 s , e,下一个区间端点为 ns ,ne 按照
s<= ns <= ne <= e时,说明下一区间已被包含在内,跳过;
s<= ns <= e <= ne时,说明下一区间被部分包含在内,更新 e 为 ne
s<= e <= ns <= ne时,说明下一区间与当前区间无交集,当 [s,e] 加入结果,同时更新 s 和 e 分别为 ns 和 ne。
代码
class Solution {
public int[][] merge(int[][] intervals) {
//按照start进行排序
Arrays.sort(intervals, (o1, o2) -> {return o1[0] - o2[0];});
List<int[]> res = new ArrayList<>();
res.add(intervals[0]);
int index = 0;//res中最后一个序号
for(int i = 1; i < intervals.length; i++){
int[] cur = intervals[i];
int[] cmp = res.get(index);
if(cmp[1] >= cur[0]) cmp[1] = Math.max(cmp[1], cur[1]);
else{
res.add(cur);
index++;
}
}
int[][] ans = new int[res.size()][];
for(int i = 0; i < res.size(); i++){
ans[i] = res.get(i);
}
return ans;
}
}
27. 不同路径 62
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
解析
d p [ i ] [ j ] dp[i][j] dp[i][j] 是到达 i, j 最多路径 ,
从上面移动下来的 f ( i , j ) = f ( i − 1 , j ) f(i, j) = f(i - 1, j) f(i,j)=f(i−1,j)
从左面移动过来的 f ( i , j ) = f ( i , j − 1 ) f(i, j) = f(i , j - 1) f(i,j)=f(i,j−1)
f ( i , j ) = f ( i − 1 , j ) + f ( i , j − 1 ) f(i, j) = f(i - 1,j) + f(i, j -1) f(i,j)=f(i−1,j)+f(i,j−1)
代码
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for(int i = 0; i < m; i++){
dp[i][0] = 1;//第 0 列 只能向下走,一条路径
}
for(int j = 0; j < n; j++){
dp[0][j] = 1;//第 0 列 只能向右走,一条路径
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
28. 最小路径和 64
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
解析
d p [ i ] [ j ] dp[i][j] dp[i][j]是到达 i, j 最小路径和 ,
从上面移动下来的 f ( i , j ) = f ( i − 1 , j ) + o [ i ] [ j ] f(i, j) = f(i - 1, j) + o[i][j] f(i,j)=f(i−1,j)+o[i][j]
从左面移动过来的 f ( i , j ) = f ( i , j − 1 ) + o [ i ] [ j ] f(i, j) = f(i , j - 1) + o[i][j] f(i,j)=f(i,j−1)+o[i][j]
f ( i , j ) = m i n ( f ( i − 1 , j ) + f ( i , j − 1 ) ) + o [ i ] [ j ] f(i, j) = min( f(i - 1,j) + f(i, j -1)) + o[i][j] f(i,j)=min(f(i−1,j)+f(i,j−1))+o[i][j]
代码
class Solution {
public int minPathSum(int[][] grid) {
int r = grid.length, c = grid[0].length;
int[][] dp = new int[r][c];
dp[0][0] = grid[0][0];
for(int i = 1; i < r; i++){
dp[i][0] = dp[i - 1][0] + grid[i][0]; // 第 0 列只能往下走
}
for(int j = 1; j < c; j++){
dp[0][j] = dp[0][j - 1] + grid[0][j]; //第 0 行只能往左走
}
for(int i = 1; i < r; i++){
for(int j = 1; j < c; j++){
dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[r - 1][c - 1];
}
}
29. 爬楼梯 70
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
3. 1 阶 + 1 阶 + 1 阶
4. 1 阶 + 2 阶
5. 2 阶 + 1 阶
解析
1.定义状态:上一个 n 级的台阶总共有多少种爬法
2.编写状态转移方程:f(n)=f(n-1)+f(n-2)
3.设置初始值:f(0)=1,f(1)=1 到达0台阶的方法有一种,就是不爬
代码
class Solution {
public int climbStairs(int n) {
if(n == 1) return 1;
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i < n + 1; i++){
dp[i] = dp[i - 1] + dp[i -2];
}
return dp[n];
}
}
30. 编辑距离 72
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
解析
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示 str1 的前 i 个字符和 str2 的前 j 个字符的编辑距离。否则就比较插入、删除和替换三种操作哪种的代价小:
-
如果 str1 的前 i - 1 个字符和 str2 的前 j 个字符相等,那么我们只需要在 str1 最后
插入一个字符就可以转化为 str2 。
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + 1 dp[i][j] = dp[i - 1][j] + 1 dp[i][j]=dp[i−1][j]+1 -
如果 str1 的前 i 个字符和 str2 的前 j - 1 个字符相等,那么我们只需要在 str1 最后
删除一个字符就可以转化为 str2 。
d p [ i ] [ j ] = d p [ i ] [ j − 1 ] + 1 dp[i][j] = dp[i][j - 1] + 1 dp[i][j]=dp[i][j−1]+1 -
如果 str1 的前 i - 1 个字符和 str2 的前 j - 1 个字符相等,那么我们要判断 str1 和 str2 最后一个字符是否相等:
-
如果相等,则不需要任何操作。 d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] dp[i][j] = dp[i - 1][j - 1] dp[i][j]=dp[i−1][j−1]
-
如果不相等,则只需要将 str1 最后一个字符
修改为 str2 最后一个字符即可。 d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j] = dp[i - 1][j - 1] + 1 dp[i][j]=dp[i−1][j−1]+1
-
代码
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m + 1][n + 1];
dp[0][0] = 0;
for(int i = 1; i < n + 1; i++){
dp[0][i] = dp[0][i - 1] + 1;
}
for(int j = 1; j < m + 1; j++){
dp[j][0] = dp[j - 1][0] + 1;
}
for(int i = 1; i < m + 1; i++){
for(int j = 1; j < n + 1; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1])) + 1;
}
}
}
return dp[m][n];
}
}
31. 颜色分类 75
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
解析
荷兰国旗问题
代码
class Solution {
public void sortColors(int[] nums) {
int less = -1, more = nums.length, index = 0;
while(index < more){
if(nums[index] < 1){
swap(nums, index++, ++less);
}else if(nums[index] > 1){
swap(nums, index, --more);
}else{
index++;
}
}
}
private void swap(int[] nums, int a, int b){
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
32. 最小覆盖子串 76
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
解释:最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。
示例 2:
输入:s = “a”, t = “a”
输出:“a”
解释:整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。
解析
使用双指针 i、j,其中 i 遍历字符串 s,j 用来寻找满足条件的位置,使得 j 到 i 的字符串刚好包含字符串 t 的所有字符。
双指针一个left 一个 right,中间夹着的就是子串,right不停往右走,一旦之间的子串符合要求,left收缩直到长度最小,当子串不符合要求的时候,right 继续往右走。
代码
class Solution {
public String minWindow(String s, String t) {
int[] map = new int[128]; //ASCII码的map
for(int i = 0; i < t.length(); i++){
map[t.charAt(i)]++;
}
String res = null;
int count = 0;//统计是否全部包含t
//i 是 快 j 是慢指针
for(int i = 0, j = 0; i < s.length(); i++){
//当前字符
map[s.charAt(i)]--;
if(map[s.charAt(i)] >= 0){
count++;
}
//慢指针有冗余字符
while(j <= i && map[s.charAt(j)] < 0) map[s.charAt(j++)]++;
if(count == t.length()){
if(res == null || res.length() > i - j + 1){
res = s.substring(j, i + 1);
}
}
}
return res == null ? "" : res;
}
}
33. 子集 78
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
解析
枚举每个元素是否选择,遍历到最后一个元素结束搜索。
代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> temp = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
dfs(nums, 0);
return res;
}
private void dfs(int[] nums, int index){
if(index == nums.length){
res.add(new ArrayList(temp));
return;
}
//选择当前元素
temp.add(nums[index]);
dfs(nums, index + 1);
//回溯
temp.remove(temp.size() - 1);
//不选择当前元素
dfs(nums, index + 1);
}
}
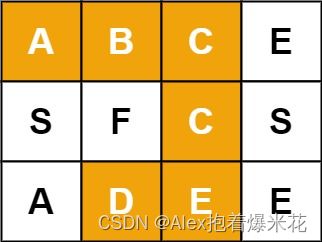
34. 单词搜索 79
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
解析
参考 岛屿的数量
枚举矩阵的每个位置作为单词的起点,只要能找到对应单词就直接返回 true。
具体在每次搜索中,可以依次尝试相邻未访问格子的字母,只要能和单词对应位置匹配,就继续向下搜索。
代码
class Solution {
public boolean exist(char[][] board, String word) {
for(int i = 0; i < board.length; i++){
for(int j = 0; j < board[0].length; j++){
if(dfs(board, word, i, j, 0)) return true;
}
}
return false;
}
public boolean dfs(char[][] board, String word, int i, int j, int index){
if(index == word.length()) return true;
if(i < 0 || i >= board.length || j < 0 || j >= board[0].length //边界条件
|| board[i][j] != word.charAt(index)) return false;
char tmp = board[i][j];
board[i][j] = '.';
boolean t1 = dfs(board, word, i - 1, j, index + 1);
boolean t2 = dfs(board, word, i + 1, j, index + 1);
boolean t3 = dfs(board, word, i, j - 1, index + 1);
boolean t4 = dfs(board, word, i, j + 1, index + 1);
board[i][j] = tmp;
return t1 || t2 || t3 || t4;
}
}
35. 柱状图中最大的矩形 84
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
解析
本题与 0042. 接雨水 解法相似,但由于计算面积需要找到当前柱子左右第一个比它小的柱子,因此栈内顺序与「接雨水」相反,即:从栈顶到栈底的高度右大到小,这样就可以得到当前高度的左右边界,遍历所有高度即可求出最大值。
代码
class Solution {
public int largestRectangleArea(int[] heights) {
Deque<Integer> stack = new ArrayDeque<>();//单调栈
int res = 0;
int[] newHeights = new int[heights.length + 1];
for(int i = 0; i < heights.length; i++){
newHeights[i] = heights[i];
}
newHeights[heights.length] = -1;//为了清空栈
for(int i = 0; i < newHeights.length; i++){
while(!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]){
int index = stack.pop();
int left = stack.isEmpty() ? -1 : stack.peek();
res = Math.max(res, (i - left - 1) * newHeights[index]);
}
stack.push(i);
}
return res;
}
}
36. 最大矩形 85
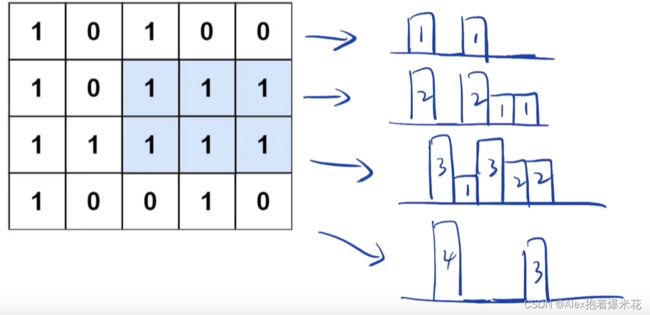
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:

输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = []
输出:0
解析
本题是 0084. 柱状图中最大的矩形 的改编版,只需在原有基础上对每一行作为 x 轴的柱状图求解即可。
代码
class Solution {
public int maximalRectangle(char[][] matrix) {
int r = matrix.length, c = matrix[0].length;
int[] height = new int[c];
int res = 0;
for(int i = 0; i < r; i++){
//对每一行统计柱状图
for(int j = 0; j < c; j++){
if(matrix[i][j] == '1') height[j]++;
else height[j] = 0;
}
res = Math.max(res, maxArea(height));
}
return res;
}
private int maxArea(int[] height){
Deque<Integer> stack = new ArrayDeque<>();
int[] newHeight = new int[height.length + 1];
for(int i = 0; i < height.length; i++){
newHeight[i] = height[i];
}
newHeight[height.length] = -1;//为了清空栈
int res = 0;
for(int i = 0; i < newHeight.length; i++){
while(!stack.isEmpty() && newHeight[i] < newHeight[stack.peek()]){
int idx = stack.pop();
int left = stack.isEmpty() ? -1: stack.peek();
res = Math.max(res, (i - left - 1) * newHeight[idx]);
}
stack.push(i);
}
return res;
}
}