计算机也能成为艺术家？(基于论文A Neural Algorithm of Artistic Style的图像风格迁移)

先不急着到达最精彩的地方，在这之前，让子弹再飞一会。

引言

卷积神经网络能做什么？ 不论是图像识别，物体检测，图像分割或是场景重建，CNN早已经在计算机视觉的各种任务上大放异彩。对于CV研究者而言，2012年就像一个分水岭。2012年以前，在CV任务上的研究重点倾向于如何设计更好的人工特征，2012年以后，研究方向发生了180度大转弯，人工特征被渐渐抛弃，取而代之的是越来越复杂，能够提取越来越丰富特征的深度学习算法，其中就包括卷积神经网络。各种论文，实验，竞赛早已证明了CNN在CV任务上的卓越能力。

但是，CNN，或者说深度神经网络却一直有一个通病，那就是同传统的机器学习算法相比，CNN实则是一个黑盒子，传统机器学习算法重在特征工程，人工调参。算法的可解释性强，相比之下CNN网络却一直缺乏合理的可解释性。

可解释性

相较于把可解释性描述为数学上把一个公式通过运用各种定理，加上严谨的推理证明的这一过程，我本人更倾向将可解释性针对于CNN的内部推理机制，而不是CNN的算法本身。(当然算法本身需要调参也比较玄学)

再回到CNN缺乏合理的可解释性上来，也就是说，对于某个任务而言，CNN完成的很出色，但是对于作为人类的我们来说，我们并不知道它到底是如何完成的这么出色的，相反，一个具有可解释性的算法，对于我们而言才是具有借鉴意义的，因为我们能够通过网络到底学到了什么，来有针对性的修改网络的结构，或是辅助人类发现无法观察到的特征。

正是由于CNN的可解释性差，自从AlexNet诞生以来，研究者们对于卷积神经网络的研究就分叉为两个方向，一个致力于挖掘CNN在各种任务上的应用，另一个则倾向于寻找CNN网络的潜在可解释性。

一种途径：特征可视化

最早基于可解释性研究的是2013年的一篇论文Visualizing and Understanding Convolutional Networks。作者将特定卷积层的激活值通过梯度上升的方法，利用反卷积映射回原图大小，从而可视化出不同的卷积核到底学到了什么样的特征表达。通过该可视化方法，作者发现越是底层的卷积学习到的特征越简单，越是深层次的卷积学习到的特征越复杂。

紧随其后，Google在2015年也发布了一个有意思的项目，叫做Deep Dream，即让CNN"做梦"，来实现一些有意思的效果。

Deep Dream的原理和论文中的可视化方法相似，通过梯度上升的方法，在反向传播时，更新的是输入图像的参数(左图)而不是网络的参数，通过迭代将卷积某一层的激活值优化到最大，最终得到的结果(右图)在某种意义上就是该卷积核所负责提取的特征：

这里的输入图像可以是任意的，假如我们优化的卷积核恰好负责提取狗的特征，那么优化之后的图像再输入预测网络时，就会被网络大概率的预测为狗，而不是人。因为优化后的图像包含了大量的神经网络所认为的狗的特征。

特征和风格，两者或许是一种东西

对于人类而言，当你看到一幅梵高的画，或是毕加索的画，你一定会一眼就认出来。如果再问你，是依据什么进行判断的，这还不简单，这两位大师的风格明显就不一样嘛。

对于风格迁移而言，算法的核心部分就是如何提取一幅图的风格。这也是其灵魂所在。但事实上，对于风格这种东西，实则是很难通过量化去表达的。传统的风格迁移算法，其原理就是从风格图中提取出某种统计模型，这些模型就代表了图像风格的某种量化表达。但这样基于人工设计的方法耗时又费力。渐渐地，人们发现卷积神经网络天然就具有这方面的能力，因为图像的风格可以表示为图像的一种内在的特征，在风格生成这方面，上述卷积特征可视化的方法就具有借鉴意义。

当然，无论是风格还是特征，它们都有一个统称——图像的纹理(texture)。

图像纹理生成

在2015年的论文 Texture Synthesis Using Convolutional Neural
Networks中，作者就提出了一种通用的算法，可以生成任意图像的纹理，方法也和前面两种类似，都是基于不更新网络参数，只更新初始噪声的梯度上升方法。一个创新之处在于，在如何量化的衡量图像风格这一问题上，作者采用了**格拉姆矩阵(Gram Matrix)**的度量方法。

格拉姆矩阵

在存数学的定义上，格拉姆矩阵被定义为n维欧式空间中任意k个向量之间两两的内积所组成的矩阵：
$$M_{Gram}=M^{T}M$$
我们知道，两个向量内积的值可以反映这两个向量之间的某种联系，运用在图像风格的度量上，就可以表示两种特征在原图上的“出现程度”以及“共现相关性”。

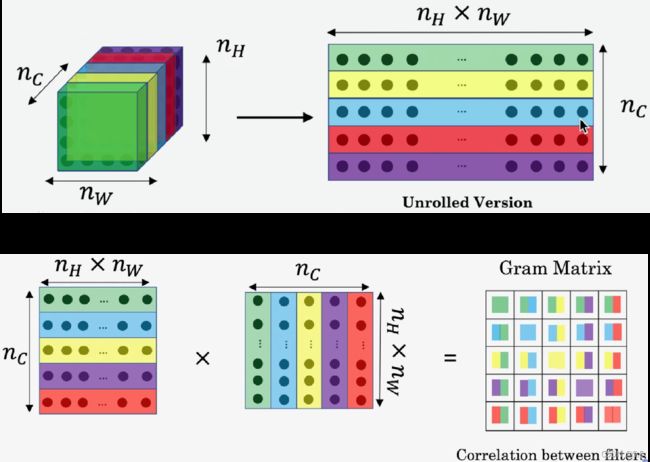
如果将一层卷积的输出作为输入，那么格拉姆矩阵就可以反映该层卷积提取的特征两两之间的关系：

如上图所示，对于某层卷积的输出，先将每个通道展平成一维张量(reshape成[C, H*W]),作为特征矩阵，再将该特征矩阵和自己的转置相乘，得到的矩阵即为特征矩阵的格拉姆矩阵，格拉姆矩阵是一个对称阵，对角线上的元素代表每个通道特征自己和自己的内积，其余的元素代表不同通道之间的两两内积。

为什么格拉姆矩阵可以反映特征之间的“出现程度”以及“共现相关性”呢，一个普遍且易于理解的解释是，卷积网络不同卷积层下每一个通道的输出实则反映了图像对于某一种特征的激活程度，图像越具有该特征，那么输出的feature map的每一个像素值就越高，将两个不同特征的激活值两两相乘，如果两个特征在原图都有出现并且特别明显，那么相乘得到的值就越高，这时候我们就认为这两个特征的共现相关性就高，相反，如果一个特征在图上比较明显而另一个特征不明显或是两个特征都不明显，那么他们相乘的值就低。这在一定的程度上就可以定义图像的风格或者说纹理。

纹理生成网络

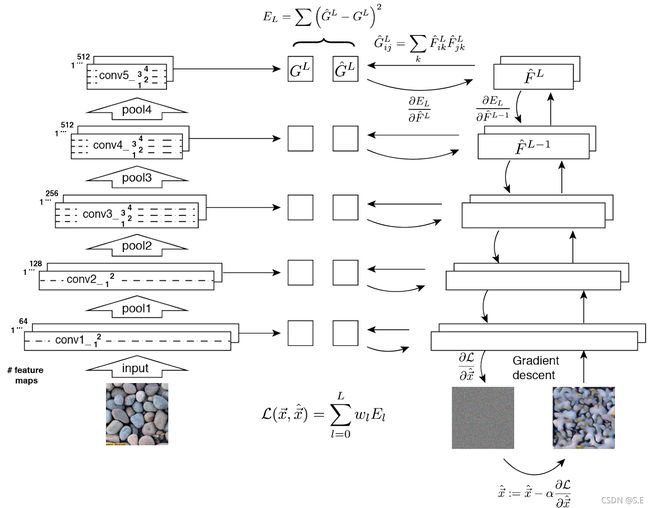
在论文中，作者采用预训练的VGG19(去掉最后用来分类的全连接层)卷积网络来提取图像特征。网络的输入包括一张风格图和一张随机初始化的噪声图。vgg19共有5个卷积Block，在每个Block的输出部分，都会计算一个输出Feature Map的Gram矩阵：
$${\hat{G}}_{ij}^L=\sum _k{\hat{F}}_{ik}^L{\hat{F}}_{jk}^L$$

纹理损失函数

对于每一层的损失，即通过优化风格图的Gram矩阵与初始噪声图的Gram矩阵的L2距离，来使得噪声图与风格图的纹理(风格)尽可能的接近：
$$E_L=\sum {\left({\hat{G}}^L-G^L\right)}^2$$
有别于梯度下降优化网络参数的方法，在图像纹理生成网络中，VGG19更像是一个先验的Encoder，在训练过程中需要冻结其内部的网络参数，与此相反，随机初始化的噪声图才是梯度下降优化的对象，对于网络的总损失，则是对每一层的损失加权求和：
$$\mathcal{L}(x,\hat{x})=\sum _{l=0}^L{w}_l{E}_l$$
纹理生成效果：

在论文中，作者给出了四张图像的纹理生成效果，可以发现，对于浅层的卷积，生成的比较单一，主要都是一些基础的颜色以及斑块，一定程度上反映了浅层卷积负责提取较为简单的特征；随着网络尺度的加深，越是深层的卷积提取的特征就更为复杂，具体。包含的语义和结构化信息更丰富。

在搜索资料的过程中，偶然发现了一个纹理合成网站，有兴趣的请移步:

BETHGE LAB · Texture Synthesis with deep CNNs

一些细节

在这里有一个细节不知大家是否注意，那就是对于前两张图像而言，网络合成的纹理和原始的图像几乎达到了真假难辨的程度，普通人如果不仔细观测或许很难发现右边的图像是合成的，但是对于第三张尤其是第四张图像而言，合成的图像和原始图像就具有很大差异。这个问题其实并不是网络收敛得不好，而是由网络的损失函数决定的。

在格拉姆矩阵的计算过程中，风格之间的度量采用向量点积的方式，也就意味着，如果将feature map的Instance维度调换位置，计算得到的Gram矩阵仍然是一致的。这就说明了一个问题，即图像的纹理特征和空间属性无关。

而对于第四张图而言，图像具有明显的空间语义信息(人，地板，显示屏)，而合成的图像把空间属性给忽略了。

从纹理合成到风格迁移

好了，讲了那么多铺垫，终于到风格迁移了吗

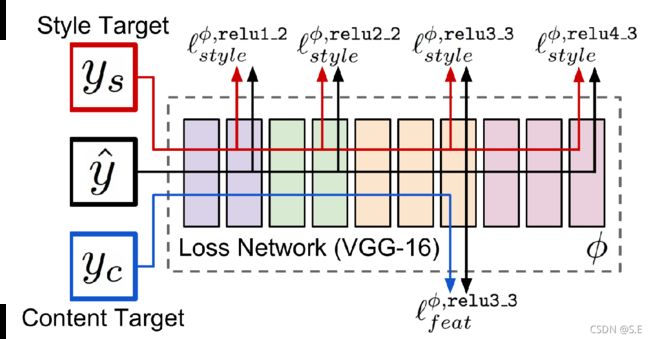
由论文A Neural Algorithm of Artistic Style所构建的图像风格迁移网络，特征提取网络仍然是VGG19，训练过程分为两个部分：一部分输入内容图像(Content Image),通过内容损失优化生成图像的内容；另一部分输入风格图像(Style Image),由风格损失优化生成图像的风格。最终优化结果便是，生成图既包含内容图的内容，又包含风格图的风格：

风格迁移网络结构：

对于风格的优化，原理以及损失和纹理合成的思想相同，可以参考纹理生成网络部分，这里就不再详细介绍了。

当然除了风格上的优化，网络还需要继续内容上的优化，使得生成的图像仍然保留内容图的基本信息。

在训练过程中，和风格优化稍有不同的是，内容的优化只选取网络的第四层卷积Block的输出，原因在于，浅层的卷积输出的feature map和原图大小相近，更容易重建出原图的内容，而深层的卷积经过多次下采样，损失了一些信息，虽然重建效果不好，但对于艺术效果来说，反而使得生成图像多具备了一些绘画质感的"灵魂"：

内容损失函数

$${\mathcal{L}}_{\text{content }}(p,x,l)=\frac{1}{2}\sum _{i,j}{\left(F_{ij}^l-P_{ij}^l\right)}^2$$

对于第l层卷积，内容损失即计算该层的内容图的feature map和噪声图的feature map的L2距离(一点都不复杂，就是你想的那样)，前面的1/2系数只是为了方便求导，也可以用权重系数代替。同风格损失一样，内容损失同样需要冻结网络参数，只优化生成图。(在论文中，只选取网络第四个卷积block的feature map参与计算内容损失)

总损失函数

$${\mathcal{L}}_{\text{total }}(p,a,x)=\alpha {\mathcal{L}}_{\text{content }}(p,x)+\beta {\mathcal{L}}_{\text{style }}(a,x)$$

将风格损失和内容损失加权求和，就是网络的总损失。

Torch代码实战

导入所需库

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision.models import vgg19
from torchvision import transforms as tf
from PIL import Image
import numpy as np
from matplotlib import pyplot as plt

device =  'cuda' if torch.cuda.is_available() else 'cpu'

超参数

α = 1    # 内容损失权重
β = 1e3  # 风格损失权重
γ = 0
EPOCH = 100 # 迭代次数
Content_layer = 4
closs, sloss = [0.],[0.]
mse_loss = nn.MSELoss(reduction='mean') # 损失函数

预处理

# 图像预处理
transform = tf.Compose([ # 喂入网络
                tf.Resize((512,512)),
                tf.ToTensor(),
                tf.Normalize([0.485, 0.456, 0.406], [1, 1, 1]),
            ])
decode = tf.Compose([  # 复原(transform逆操作)
                tf.Normalize([-0.485,-0.456,-0.406], [1, 1, 1]),       
                tf.Lambda(lambda x: x.clamp(0,1))
            ])
tensor2PIL = tf.ToPILImage()

数据读取

style_img_path = '../input/styles/style/monet.jpg'  # 风格图
content_img_path = '../input/imagesdata/old.png'    # 内容图

style_img = Image.open(style_img_path)
content_img = Image.open(content_img_path)

style_img = transform(style_img).to(device)
content_img = transform(content_img).to(device)

内容损失

# 内容损失:
class content_loss(nn.Module):
    def __init__(self):
        super(content_loss, self).__init__()

    def forward(self, content, content_target):
        c_loss = mse_loss(content, content_target)
        return c_loss

风格损失

# 计算格拉姆矩阵
def gram_matrix(x):
    # x = x.unsqueeze(0)
    b, c, h, w = x.size()
    F = x.view(b,c,h*w)
    # torch.bmm计算两个矩阵的矩阵乘法，维度必须是(batches, w, h)
    G = torch.bmm(F, F.transpose(1,2))/(h*w)
    return G
    
    
# 风格损失:
class style_loss(nn.Module):
    def __init__(self):
        super(style_loss, self).__init__()

    def forward(self, gram_styles, gram_targets):
        s_loss = 0
        for i in range(5):
            # N = gram_styles[i].shape[-1]
            # M = style_features[i].shape[-1]
            s_loss += mse_loss(gram_styles[i],gram_targets[i])
        return s_loss

• 平滑损失(缓解生成图在优化时产生突变的噪声)(感觉效果不明显就给去了)

# # 平滑损失:
# class smooth_loss(nn.Module):
#     def __init__(self):
#         super(smooth_loss, self).__init__()

#     def forward(self, x):
#         smoothloss = torch.mean(torch.abs(x[:, :, 1:, :]-x[:, :, :-1, :])) + torch.mean(torch.abs(x[:, :, :, 1:]-x[:, :, :, :-1]))
#         return smoothloss

总损失

# 总损失:
class total_loss(nn.Module):
    def __init__(self):
        super(total_loss, self).__init__()

    def forward(self, content, content_target, gram_styles, gram_targets, image, α, β):
        closs = content_loss()
        sloss = style_loss()
        smooth = smooth_loss()
        c = closs(content, content_target)
        s = sloss(gram_styles, gram_targets)
        t = α * c + β * s # + γ * smooth(image)
        return t, α * c, β * s

读取网络中间层输出 torch.register_forward_hook()

# 获取网络某层的输出
def get_features(module, x, y):
    features.append(y)
    
    
# 只需要卷积层
VGG = vgg19(pretrained=True).features.to(device)

for i, layer in enumerate(VGG):
    # 获取forward过程中网络特定层的输出, 21层用作计算内容损失, 其余用作计算风格损失
    if i in [0,5,10,19,21,28]:
        VGG[i].register_forward_hook(get_features) 
    # 将网络中的最大池化全部替换为平均池化，论文中表示这样生成效果更好
    elif isinstance(layer, nn.MaxPool2d):
        VGG[i] = nn.AvgPool2d(2)

基于迭代优化生成的风格迁移方法不需要大量的数据集，只需要一张风格图和一张内容图，在每一次迭代训练的过程中，风格图和内容图都是相同的，因此我们无需每次迭代都循环地提特征：

VGG.eval()
# 由于优化的是生成图，因此冻结网络的参数
for p in VGG.parameters():
    p.requires_grad = False

# 内容损失需要参考的网络输出层
features = []  # features用来保存网络中间层输出
VGG(content_img.unsqueeze(0))
content_target = features[Content_layer].detach() 
# 风格损失需要参考的网络输出层
features = []
VGG(style_img.unsqueeze(0))
s_targets = features[:4] + features[5:] 
# 计算风格图的格拉姆矩阵:
gram_targets = [gram_matrix(i).detach() for i in s_targets]

初始图像可以是噪声图也可以是内容图，最后的优化效果也有不同

# 优化图像就是原图
image = content_img.clone().unsqueeze(0)      
# 优化图像是随机噪声
# image = torch.randn(1,3,512,512).to(device)   

由于两张图像就是整个数据集，因此就不存在batches这一东西，每一次迭代优化就是整个损失空间。所以对于优化器的选择可以大胆一点，干脆直接采用牛顿二阶优化方法(求二阶导，更精确的逼近)，并设置大学习率，能够缩短收敛时间：

# 牛顿二阶优化法(学习率为1.1)
optimizer = optim.LBFGS([image.requires_grad_()], lr=1.1)  

训练(生成)

for step in range(EPOCH):

    features = []
    # LBFGS需要重复多次计算函数，因此需要传入一个闭包去允许它们重新计算你的模型。这个闭包应当清空梯度，计算损失，然后返回
    def closure():
        optimizer.zero_grad()

        VGG(image)
        t_features = features[-6:]
        # 内容层
        content = t_features[Content_layer]  
        # 风格层  
        style_features = t_features[:4] + t_features[5:] 
        t_features = []
        # 计算风格层的格拉姆矩阵
        gram_styles = [gram_matrix(i) for i in style_features]  

        # 计算损失
        loss = total_loss()
        tloss, closs[0], sloss[0] = loss(content, content_target, gram_styles, gram_targets, image, α, β)
        tloss.backward()
        return tloss

    optimizer.step(closure)
    

    
	# 保存生成图像
    if step % 2 == 0:
        print('Step {}: Style loss: {:.8f} Content loss: {:.8f}'.format(step, sloss[0], closs[0]))
        temp = decode(image[0].cpu().detach())
        temp = tensor2PIL(temp)
        temp = np.array(temp)
        plt.imsave('result.jpg',temp)

效果展示

只优化风格损失函数(α = 0, β = 1e3 )

只优化内容损失函数(α = 1, β = 0)

风格迁移效果展示(太惊艳了)