114. 二叉树展开为链表
给定一个二叉树,原地将它展开为一个单链表。
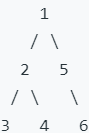
例如,给定二叉树
将其展开为:
思路一:
先来一个前序遍历把所有结点存在一个列表中,然后遍历链表,把所有结点用右指针串起来
1 /**
2 * Definition for a binary tree node.
3 * public class TreeNode {
4 * int val;
5 * TreeNode left;
6 * TreeNode right;
7 * TreeNode() {}
8 * TreeNode(int val) { this.val = val; }
9 * TreeNode(int val, TreeNode left, TreeNode right) {
10 * this.val = val;
11 * this.left = left;
12 * this.right = right;
13 * }
14 * }
15 */
16 class Solution {
17 public void flatten(TreeNode root) {
18 if(root == null)
19 return ;
20 List list = new ArrayList<>();
21 TreeNode top = root;
22 Stack stack = new Stack<>();
23 // 先来一个前序遍历把所有结点存在一个列表中
24 while(!stack.empty() || top != null){
25 while(top != null){
26 list.add(top);
27 stack.push(top);
28 top = top.left;
29 }
30 top = stack.pop();
31 top = top.right;
32 }
33
34 // 遍历链表,把所有结点用右指针串起来
35 int n = list.size();
36 for(int i = 0; i < n; i++){
37 if(i > 0){
38 list.get(i - 1).right = list.get(i);
39 }
40 list.get(i).left = null;
41 }
42 }
43 }
力扣测试:时间为2ms, 空间为39MB
复杂度分析:
时间复杂度:一次存,一次遍历,相当于遍历了两次二叉树,所以时间复杂度为O(n), n为节点个数
空间复杂度:列表的大小,所以为O(n)
思路二:
1. 把当前结点的右子树挂到左子树最右边的结点上
2. 把左子树挂到右子树上、
3. 更新当前结点的右子树为新的当前结点,重复上面的操作,直到当前结点为空
1 class Solution {
2 public void flatten(TreeNode root) {
3 TreeNode cur = root;
4 while(cur != null){
5 // 如果左子树为空,直接进入下个结点
6 if(cur.left == null){
7 cur = cur.right;
8 }else{
9 // 如果左子树不为空,找到它最右边的结点
10 TreeNode leftRight = cur.left;
11 while(leftRight.right != null){
12 leftRight = leftRight.right;
13 }
14 // 将右子树挂到这个结点上
15 leftRight.right = cur.right;
16
17 // 将左子树挂到右子树的位置
18 cur.right = cur.left;
19 cur.left = null;
20
21 // 更新cur指针
22 cur = cur.right;
23 }
24 }
25
26 }
27 }
力扣测试时间为:1ms, 空间为39.2mb
复杂度分析:
这个时间复杂度不太好判断,我觉得应该是O(nlogn),首先总体对每个结点必须访问一次,所以是O(n), 其次内层循环中每次都必须找到左子树最右边的结点,我觉得这个复杂度应该是O(logn),所以我觉的时间复杂度是O(nlogn)
空间复杂度为O(1)
思路三:巧用后序遍历(速度最快)
1. 右、左、根的后序遍历,遍历结果为6->5->4->3->2->1
2. 使用p->right = pre, 即可把逆序编程正序,变为把 1->2->3->4->5->6,pre结点刚好是p结点的左结点,所以不用担心左结点会丢失,
1 class Solution {
2 public void flatten(TreeNode root) {
3 // 右、左、根的后序遍历,遍历结果为6->5->4->3->2->1
4 // 使用p->right = pre, 即可把逆序编程正序,变为把 1->2->3->4->5->6,pre结点刚好是p结点的左结点,所以不用担心左结点会丢失,
5 postTraversal(root);
6 }
7 public TreeNode pre = null;
8 public void postTraversal(TreeNode p){
9 if(p != null){
10 postTraversal(p.right);
11 postTraversal(p.left);
12 p.right = pre;
13 p.left = null;
14 pre = p;
15 }
16 }
17 }
力扣测试时间为0ms, 空间为39.8MB
复杂度分析:
时间复杂度为:仅仅是一次后序遍历,所以复杂度为O(n)
空间复杂度:方法栈最大递归层数为树的高度,所以空间复杂度为O(n)
思路四:利用栈
借助一个栈,每次先把右子树压入栈,然后把左子树压入栈,这样每次左子树都会先弹栈,直接把根的右子树指向这个弹出的左子树,因为右子树已经被压入栈中了,所以右子树不会丢失
1 class Solution {
2 public void flatten(TreeNode root) {
3 Stack stack = new Stack();
4 if(root != null){
5 stack.push(root);
6 }
7 TreeNode pre = null;
8 while(!stack.empty()){
9 TreeNode top = stack.pop();
10 if(top.right != null){
11 stack.push(top.right);
12 }
13 if(top.left != null){
14 stack.push(top.left);
15 }
16 // 直接把根的右子树指向这个弹出的左子树
17 if(pre != null){
18 pre.right = top;
19 pre.left = null;
20 }
21 pre = top;
22 }
23 }
24 }
力扣测试时间为2ms, 空间为39.7MB
复杂度分析:
时间复杂度:对每个结点都出栈一次,所以时间复杂度为O(n)
空间复杂度:栈的大小即为空间的花费,这里栈同时存储的是同一层的结点,所以最坏情况下,当树只有两层时,空间复杂度为O(n/2),所以空间复杂度为O(n)
思路参考:
https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--26/