数据结构 —— 堆(超详细图解 & 接口函数实现)
系列文章目录
数据结构 —— 顺序表
数据结构 —— 单链表
数据结构 —— 双向链表
数据结构 —— 队列
数据结构 —— 栈
数据结构 —— 堆
数据结构 —— 二叉树
数据结构 —— 八大排序
文章目录
- 系列文章目录
- 前言
- 一、示例问题:层级管理
-
- 1.层级管理分配
- 2.逻辑示意图
- 3.堆的引入
- 二、堆的概念
-
- 1.定义
- 2.结构
- 3.存储
- 三、堆的接口函数
-
- 1.初始化堆
- 2.判断空堆
- 3.堆形态插入数据
- 4.堆形态删除顶部
- 5.堆顶元素
- 6.堆的元素个数
- 7.堆的销毁
- 四、总结
前言
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。数据结构是一种十分优秀的解决实际问题的模板,是先进思想的结晶。博主将会用代码结合大量图解,对数据结构进行深度剖析,以便大家更好的学习数据结构的思想。
一、示例问题:层级管理
1.层级管理分配
假如你是一个班主任,你为了方便人员的管理,需要一些有能力的同学担任班长和组长,一个职位最多管理两个同学
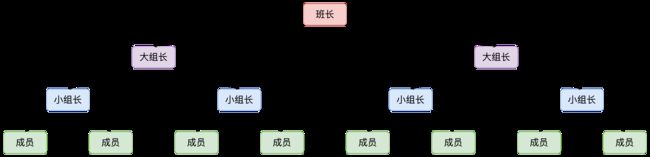
2.逻辑示意图
这里由数值表示能力,数值越大能力越强,数值越小能力越弱
- 班长 > 自己班的两个大组长
- 大组长 > 自己组的两个小组长
- 小组长 > 自己组的两个成员
注意:某组大组长不一定大于其他组的小组长或成员,同理某组小组长也不一定大于其他小组的成员
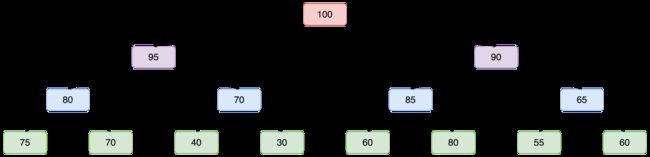
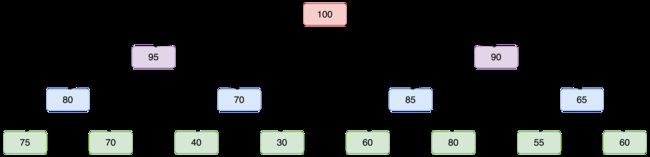
3.堆的引入
堆的引入:父节点永远大于其子节点,或父节点永远小于其子节点的数据结构
二、堆的概念
1.定义
堆:将所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树。
2.结构
堆的结构类型:二叉树的顺序存储结构
// 二叉树的顺序表结构
typedef int HPDataType;
// 顺序表结构
typedef struct Heap {
HPDataType *array;
int size;
int capacity;
} Heap;
3.存储
存储:用动态开辟的顺序表来存储
逻辑结构
物理结构
![]()
三、堆的接口函数
1.初始化堆
对队列的内容进行初始设置
// 堆的初始化
void HeapInit(Heap *php) {
assert(php);
php->array = NULL;
php->capacity = php->size = 0;
}
2.判断空堆
判断这个堆是否为空
// 堆的判空
int HeapEmpty(Heap *php) {
assert(php);
return php->size ? false : true;
}
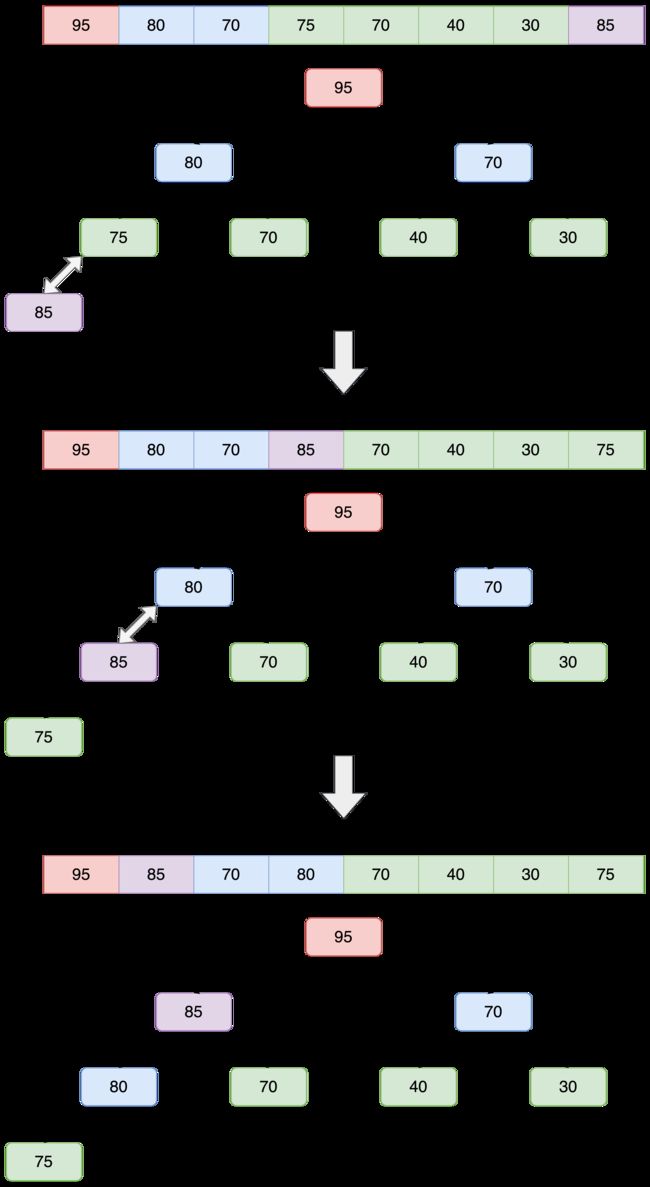
3.堆形态插入数据
插入 x 并保持堆的形态
思想精髓:
- 将插入的值与它的父节点进行比较,将大的值向上交换
- 经过多次比较交换,就维持了堆的形态
void HeapPush(Heap *php, HPDataType x) {
assert(php);
// 判断容量
if (php->size == php->capacity) {
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType *newSpace = (HPDataType *)realloc(php->array, newCapacity * sizeof(HPDataType));
if (newSpace == NULL) {
perror("realloc fail:");
}
php->array = newSpace;
php->capacity = newCapacity;
}
php->array[php->size] = x;
php->size++;
// 算法 向上调整
AdjustUp(php->array, php->size - 1);
}
// 算法 向上调整
void AdjustUp(HPDataType *array, int child) {
while (child > 0) {
int parent = (child - 1) / 2;
if (array[child] > array[parent]) {
Swap(&array[child], &array[parent], sizeof(HPDataType));
child = parent;
} else {
break;
}
}
}
// 算法 内存交换
void Swap(void *A, void *B, int size) {
while (size--) {
char tmp = *(char *)A;
*(char *)A = *(char *)B;
*(char *)B = tmp;
A = (char *)A + 1;
B = (char *)B + 1;
}
}
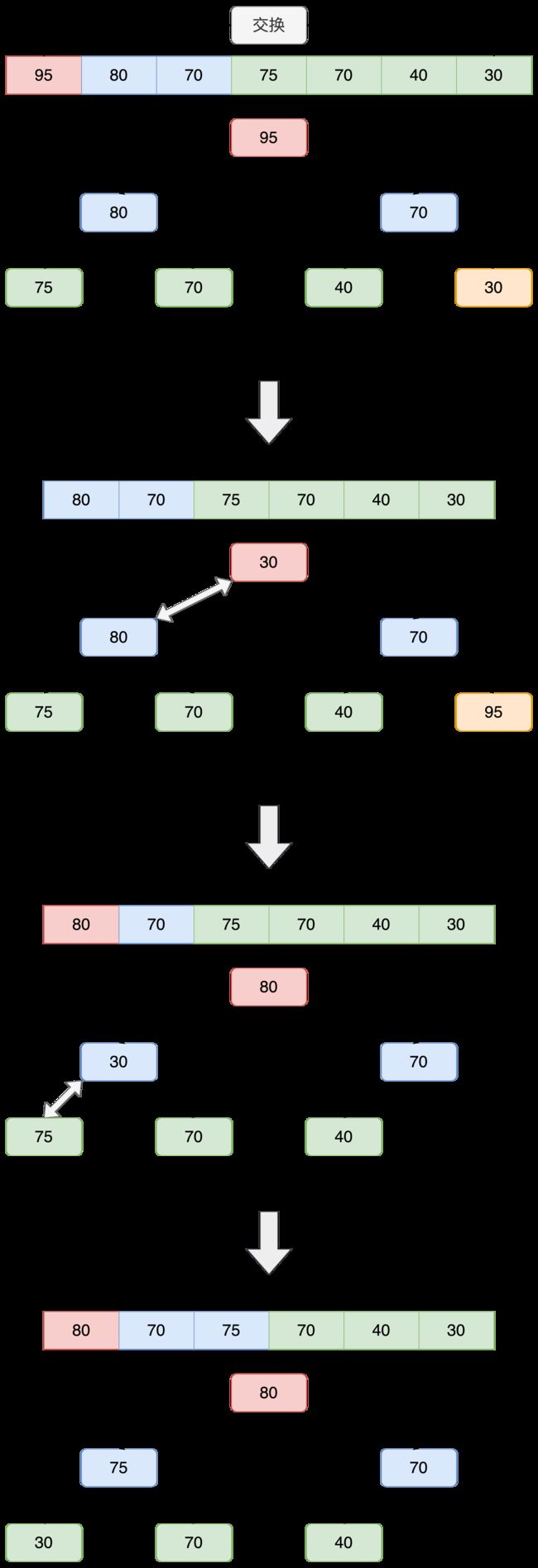
4.堆形态删除顶部
删除位于堆顶的数据,并维持堆形态
思想精髓:
- 将开头和结尾交换
- 顺序表大小减一,就将原先堆顶位置的 (最大 或 最小) 值删除成功
- 将现在堆顶的值向下调整,重新维持堆的形态
// 堆的删除
void HeapPop(Heap *php) {
assert(php);
// 将开头和结尾交换
Swap(&php->array[0], &php->array[php->size - 1], sizeof(HPDataType));
// 删除结尾
php->size--;
// 算法 向下调整
AdjustDown(php->array, php->size, 0);
}
// 算法 向下调整
void AdjustDown(HPDataType *array, int size, int parent) {
int child = parent * 2 + 1;
while (child < size) {
// 找出最小的孩子
if (child + 1< size && array[child + 1] CMP array[child]) {
child++;
}
// 判断下调
if (array[child] CMP array[parent]) {
Swap(&array[child], &array[parent], sizeof(HPDataType));
parent = child;
child = parent * 2 + 1;
} else {
break;
}
}
}
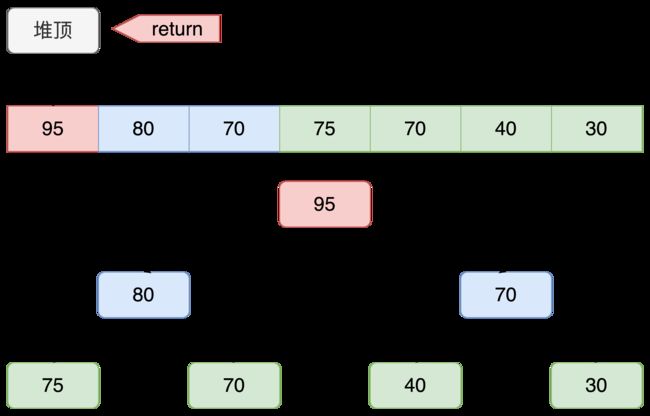
5.堆顶元素
获取堆顶位置的值
// 取堆顶的数据
HPDataType HeapTop(Heap *php) {
assert(php);
assert(!HeapEmpty(php));
return php->array[0];
}
6.堆的元素个数
获取堆中有效元素个数
// 堆的数据个数
int HeapSize(Heap *php) {
assert(php);
return php->size;
}
7.堆的销毁
释放堆申请的空间
// 堆的销毁
void HeapDestory(Heap *php) {
assert(php);
free(php->array);
php->array = NULL;
php->capacity = php->size = 0;
}
四、总结
堆是解决实际问题时极其常用的一种数据结构,是非常重要的解决问题的方式。堆的各种接口的复现,有利于更好的学习数据结构的思想,有利于开阔视野,学习前辈的智慧结晶。对我们后续解决实际问题也会有很大帮助。