回溯+剪枝算法（详细原理+代码推理过程）

理解顺序：枚举法 --> 递归/回溯法 --> 剪枝 （算法思想通用所有语言，这里采用主要Java书写）

枚举法：

将问题的所有可能的答案一一列举，然后根据条件判断此答案是否合适，合适就保留，不合适就丢弃。
例：在一个陌生的国度，有5种不同的硬币单位：15、23、29、41和67（分）。寻找所有组成18元8分（即1808分）的可能组合。假定对于所有面值的硬币你都有足够的硬币。
解：这道题也是一道经典的用枚举法求解的题。首先15分的硬币从0(最少)到1808/15种(最多)；同理23分硬币0 ~ 1808/23(做除法)；29分硬币0 ~ 1808/29；41分硬币0 ~ 1808/41；67分硬币0 ~ 1808/67；这样15、23、29、41、67分硬币只需满足15 * i+23 * j+29 * k+41 * h+67 * s=1808就是符合条件的组合；其中i,j,k,h,s都是在对应的硬币的范围之内(最少到最多)；

for(int i=0;i<=n/15;i++)//15分硬币
 {
  for(int j=0;j<=n/23;j++)//23分硬币
  {
   for(int k=0;k<=n/29;k++)//29分硬币
   {
    for(int h=0;h<=n/41;h++)//41分硬币
    {
     for(int s=0;s<=n/67;s++)//67分硬币
     {
      if(i*15+j*23+k*29+h*41+s*67==n) //判断
      {
       printf("15分硬币%d个，23分硬币%d个,29分硬币%d个，41分硬币%d个，67分硬币%d个\n",i,j,k,h,s)；
     }
     }
    }
   }
  }
 }

缺陷：
用枚举法解题的最大的缺点是运算量比较大，解题效率不高，如果枚举范围太大（一般以不超过两百万次为限），在时间上就难以承受。但 [3] 枚举算法的思路简单，程序编写和调试方便，比赛时也容易想到，在竞赛中，时间是有限的，我们竞赛的最终目标就是求出问题解，因此，如果题目的规模不是很大，在规定的时间与空间限制内能够求出解，那么我们最好是采用枚举法，而不需太在意是否还有更快的算法，这样可以使你有更多的时间去解答其他难题。

回溯算法：

例题：给定两个整数n和k，返回1…n中所有可能的k个数的组合
输入：n=4，k=2
输出：n[ [2,4]，[3,4]，[2,3]，[1,2]，[1,3]，[1,4] ]
解释：n为4，则待选数组为[ 1 2 3 4 ]
先取1，然后依次取2,3,4,。再取2，然后再依次去3,4…

这道题如果用纯枚举法，当k=2时，用两层for循环就可以解决，当k=3时，可以再嵌套一层。但当k=100时，意味着100层for循环。
这意味着代码的繁琐，所以用回溯的方法来递归解决嵌套层数的问题。以下为回溯算法的大体模板（本质是这个，但具体问题具体变形）

result 路径数组 //用于存放所有满足条件的数据
void backtrack(路径,选择列表){
	if(满足结束条件){ //第一步，如果满足结束条件，就添加数据，并结束递归
    	result.add(路径);
        return;
    }
    //如果不满足，则继续执行
    for(在选择列表中 枚举 各种情况){ //在选择列表中 枚举 各种情况。并在选择这种情况的时候，标记出这种情况已经被使用过
        做选择; //
        backtrack(路径,选择列表); //然后进行递归，直到满足结束条件，跳出递归。（注意：这一次递归，当前情况已被改变）
        撤销选择; //然后我们撤销对这种递归的情况的改变
    }
}

return result;

递归原理：在寻找当前情况下可能满足条件的结果，当它寻找完成后，就跳出了递归（遇到return）

这样，就可以暴力枚举出这种情况下我们可以进行的所有选择。最后，当所有的情况被判断完之后程序结束，返回最后的结果数组
很多回溯算法，也会适合动态规划以及记忆体搜索等算法

回溯算法是什么：一个纯暴力的搜索算法，不是什么高效算法
回溯和递归相辅相成，二者缺一不可。通常来说，递归的下面就是回溯
使用背景：有些问题纯暴力（一层一层for循环）搜索不出来，必须用回溯
能解决的问题：
1、组合问题：如上面的例题：给一个数组如[ 1,2,3,4,5 ]，选出所有的2组合，如1,2、1,3、1,4等等
2、切割问题：给一个字符串，问有几种切割的方式，可能再给一些切割条件（如怎么切割才能达到所有的子串都是回文子串）
3、子集问题：[ 1,2,3,4 ]的子集有1、2、3、4、1,2、1,3、1,4等等
4、排列问题：组合不强调元素顺序，排列强调。如 [ 1,2 ] 的排列有1,2和2,1 而组合可能只有1,2或2,1（因为组合无序，所以1,2和2,1等价）
5、棋盘问题：n皇后、解数组

建议用图形来理解回溯法，纯脑想容易混乱。回溯法可以抽象为一个树形结构（一个n叉树）

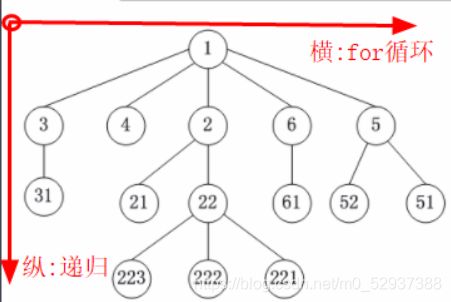
一般来说树的宽度就是我们在回溯法中处理的集合的大小（这里通常用for循环进行遍历）
而树的深度就是递归的深度（因为递归是由终止的，终止后就一层一层的向上返回）

代码构造：
回溯法一般采用void backtrack（不返回东西），参数一般是比较多的（开始时很难都确定下来，在写逻辑时，想用什么就添加上即可）
先添加终止

void backtrack(路径,选择列表){ 
	if(终止条件) { 
         收集结果 //如收集[1,2,3,4]的子集之一[1,2] 
         return; 
     }

然后一个for循环，用来处理集合里的每一个元素

    for(集合元素) { 
        处理节点  //作用：如收集[1,2,3,4]的子集之一的[1,2]，就是先在这里被存进了一个数组，在接下来递归时进入 收集结果 中 
        递归
        回溯操作 //撤销 处理节点 的操作。
    }
}
return;

回溯操作：为什么好不容易得到了一个有用的节点，还要进行 撤销节点 的操作呢：
如收集[1,2,3,4]的子集，假设我们有1，取了2，这是 [ 1, 2 ] 是一个我们需要的结果，该数据到达收集结果中后，
进行回溯，就是把取了2这个操作取消掉，这样才能再取3时数据为 [ 1,3 ] 而不是 [ 1,2,3 ] 。同理，存完 [ 1,3 ] 后再取消取了3的操作，取4
所以，有了回溯，我们才能把所有的情况的都取出来（这是纯暴力for循环嵌套所做不到的）

例题：leetcode 77.组合：给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
这道题如果用纯暴力算法for循环嵌套，那么层数无限，根本写不出来，只能用回溯。
这里以n=4，k=2为例做树形结构图

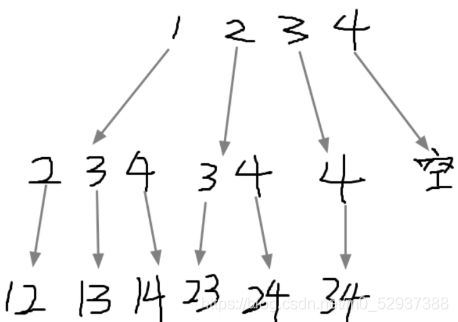
我们需要确定(1)、递归函数的参数和返回值(2)、递归的终止条件（处理不好就是死循环）(3)、单层递归逻辑
对（1）：首先我们需要最基本的n，k。在上图中进入第次个递归时是怎么做到从3开始而不是从2开始呢：用indexstart来表示起始点

int[] path = new int[999]; //我们最终要确定的东西就是如1，2、1，3、1,4..的组合，可以用一维数组储存一个组合
int[][] result = new int[2][999]; //最终我们用一个二维数组来储存所有的一维数组，也就是所有的可能组合
void backtrack(int n,int k,startindex){ 
	
}
return result; 

对（2）：因为我们需要的最终结果是如[1,2]、[1,3]、[1,4]的一维数组，所以当path的长度等于k时，就算是满足结束条件

if(path.length == k ){ //数组用.length、集合用.size()方法、字符串用.length()方法;
    	result.add(path);
        return;
}

对（3）：在树结构图里每一个节点就是一个for循环

for(i = startindex ;i <= n ;i++) {
    path.push(i); //假设现在从1开始，先将1记录（这里是第一次for循环）
    backtrack(n,k,i+1); 
    //开始递归，不满足结束条件，进入第二次的for循环(此时startindex等于2)，再记录2。再次递归，达成结束条件，return。
    //回到第二次for循环，进入这里的下一行代码开始回溯
    path.pop(); 
    //开始回溯，把刚才记录的2弹出去。然后for循环里i+1，再次递归，记录3。达成结束条件...直至12,13,14都被记录完，for循环结束，
    //这一次递归轮回彻底结束，回到第一次的for循环。进行回溯，弹出1，i+1让i变成2，记录2，开始递归...
}

剪枝：

以n=4，k=4为例：先做图表示剪枝原理

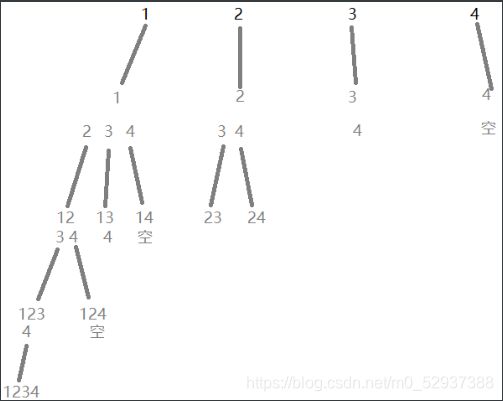
这里我们可以发现，当第一行中以2开始时，剩下的只有34，一共才3个元素，组不成4个。所以这一条分支可以剪掉
（好处：这条分支的下面还有很多衍生分支，相当于都剪掉了，节省运算）
以此可以得出，第一行2开头往右的所有分支（第一行的3和4）也都可以剪掉，节省运算
同理，第一行1开头的分支的衍生分支中，到第三行时，13开头的只剩4，可以剪掉，其右侧也都可以剪掉
同理…
代码实现：

void backtrack(int n,int k,int startindex){
	if(path.length == k ){ //数组用.length、集合用.size()方法、字符串用.length()方法;

    //for(i = startindex ;i <= n ;i++) { 剪枝就在这里进行操作，i=1时可以继续，i=2时已经没必要继续，所以换成下行的形式
    for(i = startindex ;i <= n-(k-path.size)+1 ;i++) {
        path.push(i); 
        backtrack(n,k,i+1);
        path.pop(); 
	}
}

n-(k-path.size)+1 为什么要这么取：
这个值是能进行搜索的最大值：举个例子，n=4，k=3，还未存数(path.size=0)时，代入上式最后=2。符合实际情况，从1开始，还有234共4个数可以满足k=3，从2开始，还有34共3个数也满足k=3，但从3开始就不行了，所以这个公式求出的是搜索最大值

以下为leetcode上别人的代码，链接在底下

//77.组合
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

public class Solution {

    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int index, Deque<Integer> path, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 只有这里 i <= n - (k - path.size()) + 1 与参考代码 1 不同
        for (int i = index; i <= n - (k - path.size()) + 1; i++) {
            path.addLast(i);
            dfs(n, k, i + 1, path, res);
            path.removeLast();
        }
    }
}
//链接：https://leetcode-cn.com/problems/combinations/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-ma-/

代码效果：