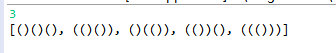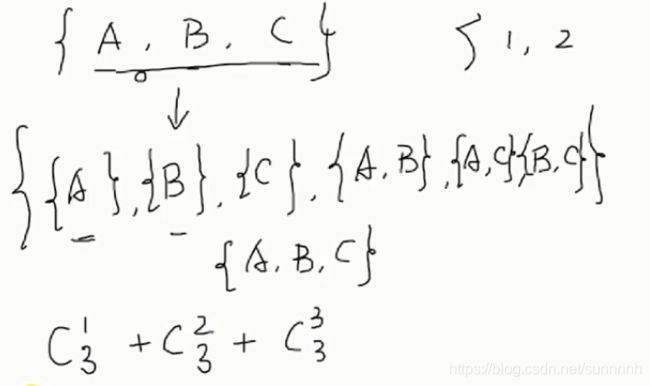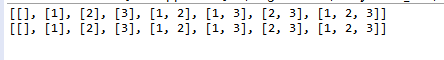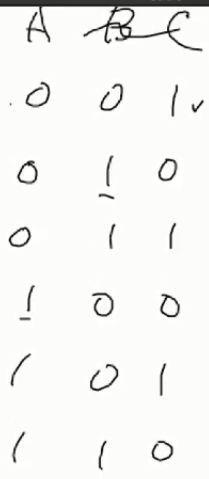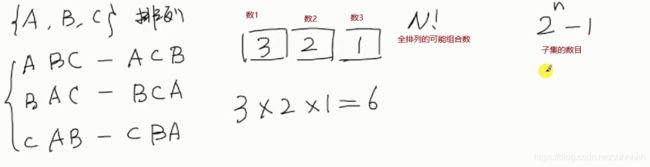7.2逐步生成结果类问题之 非数值型 ---- 第7章 深入递归(深搜,回溯,剪枝等)----求合法括号、子集、全排列
例1 合法括号
方法一:递归
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
public class Main {
/*
* Set集合去重复。注意:集合是引用类型!!不能用等号赋值!!
* */
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
Set ans = getAns(n);
System.out.println(ans);
}
private static Set getAns(int n) {
Set a = new HashSet();
if(n==1) {//只有一个括号
a.add("()");
return a;
}
Set newa = getAns(n-1);//获取n-1个括号时的组合数
for (String str : newa) {//在n-1个括号的基础上加括号。有三种可能
a.add("()"+str);//左边加括号
a.add(str+"()");//右边加括号
a.add("("+str+")");//两边加括号
}
return a;
}
}
方法二:迭代
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
public class Main {
/*
* Set集合去重复
* */
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
Set ans = getAns(n);
System.out.println(ans);
}
private static Set getAns(int n) {
Set a = new HashSet();
a.add("()");
if(n==1) return a;
for(int i=2;i<=n;i++) {//括号数目累积到n
Set newa = new HashSet();
for (String str : a) {//每次添加括号时,更新每个集合中括号的组合
newa.add("()"+str);
newa.add(str+"()");
newa.add("("+str+")");
}
a=newa;//更新当前括号集合a
}
return a;
}
}
例题2 子集生成
![]() (非空子集)
(非空子集)
类似上题加括号,是加左、加右、加外的问题
子集生成就是针对某些子集,选和不选的问题
两种方法:递归或迭代
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
public class Main {
/*
* Set集合去重复
* */
public static void main(String[] args) {
int[] a = {1,2,3};//获取数组a中不重复的子集组合
int n = a.length;//总的元素个数
int cur=n-1;//当前加入的元素下标
Set> set = getSubs1(a,n,cur);//方法一:递归
System.out.println(set);
System.out.println(getSubs2(a, n));//方法二:迭代
}
/*方法一:递归
* a:获取数组a中所有的子集,包含空寂
* n:总的元素个数
* cur:当前加入的元素a[cur]
* */
private static Set> getSubs1(int[] a, int n, int cur) {
Set> newSet = new HashSet<>();
if(cur==0) {//处理第一个元素a[0]
Set s1 = new HashSet<>();//1.空集
Set s2 = new HashSet<>();
s2.add(a[0]);
newSet.add(s1);//分别将空集和只含第一个元素的集合加入
newSet.add(s2);
return newSet;
}
Set> oldSet = getSubs1(a, n, cur-1);//加入前n-1个元素之后的集合
for (Set set : oldSet) {
newSet.add(set);//将当前的集合set加入新集合newSet
Set clone = (Set) ((HashSet)set).clone();//克隆当前集合set中的内容
clone.add(a[cur]);//将当前元素a[cur]加入当前集合set
newSet.add(clone);//将加入当前元素的集合 加入到 大集合中
}
return newSet;
}
/*
* 方法二:迭代
* */
private static Set> getSubs2(int[] a, int n) {
Set> ans = new HashSet();
ans.add(new HashSet<>());//将大集合初始化为只含 一个空集的集合
for(int i=0;i> newSet = new HashSet();//存放当前新的大集合
for (Set set : ans) {//遍历之前的集合,全部克隆一遍。并将当前元素加入每个小集合
newSet.add(set);//将当前集合加入
Set clone = (Set) ((HashSet)set).clone();//再将当前元素加入集合后,放入大集合newSet
clone.add(a[i]);
newSet.add(clone);//加入新的大集合
}
ans = newSet;
}
return ans;
}
}
例3 子集生成之二进制法(获取子集的第三种方法)
import java.util.ArrayList;
import java.util.Arrays;
public class Main {
/*
* Set集合去重复
* */
public static void main(String[] args) {
int[] a = {1,2,4};//获取数组a中不重复的子集组合
int n = a.length;//总的元素个数
ArrayList> ans= getAns(a,n);
System.out.println(ans);
}
/*
* 方法三:子集生成之二进制法
* 对于含有n个元素的集合,可生成的子集个数为2^n(包含空集)
* 因此只需判断从0~n-1位上是否为1,如果第i位为1 表示a[i]在子集中
*
* */
private static ArrayList> getAns(int[] a, int n) {
Arrays.sort(a);//对数组a进行升序排列。由于下面是从高位开始检查,故得到的结果集是逆序
ArrayList> res = new ArrayList();
for(int i=(int) Math.pow(2, n)-1;i>=0;i--) {//较大的数字~0 (最多有2^n个子集)
ArrayList s = new ArrayList();//针对每一个i建立一个集合
for(int j=n-1;j>=0;j--) {//检查哪一位上的数字为1,从高位开始检查
if(((i>>j)&1)==1) {
s.add(a[j]);
}
}
res.add(s);
}
return res;
}
}
例4 全排列
对n个数进行全排列,可能的组合数目:n!
方法一:
import java.util.ArrayList;
public class Main {
/*
* Set集合去重复
* */
public static void main(String[] args) {
String str="ABC";
ArrayList res = getPermutation1(str);//对串str进行全排列
System.out.println(res);
}
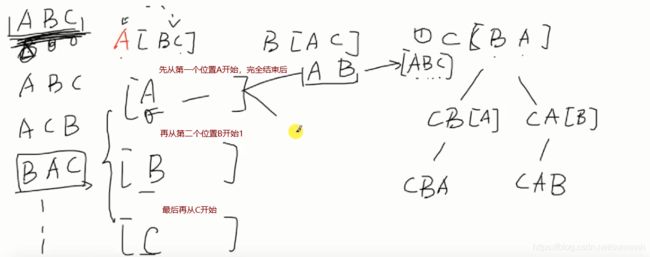
/*方法一:逐步生成大法--迭代法
* (1)初始化集合只包含第一个字符
* (2)依次向集合中加入剩余的字符
* (2.1)依次遍历集合中已有的排列
* (2.1.1)向当前排列的 前面位置加入当前字符
* (2.1.2)向当前排列的 后面位置加入当前字符
* (2.1.3)向当前排列的 所有可能的中间位置加入当前字符
*
* */
private static ArrayList getPermutation1(String str) {
int len = str.length();
ArrayList res = new ArrayList<>();
res.add(str.charAt(0)+"");//(1)初始化集合只包含第一个字符
//(2)依次向集合中加入剩余的字符
for(int i=1;i newRes = new ArrayList<>();
char c= str.charAt(i);//获取要插入的字符
//(2.1)依次遍历原集合中已有的排列
for (String s: res) {
//(2.1.1)向当前排列的"前面位置"加入当前字符
newRes.add(c+s);
//(2.1.2)向当前排列的 "后面位置"加入当前字符
newRes.add(s+c);
//(2.1.3)向当前排列的 所有可能的"中间位置"加入当前字符
for(int j=1;j<=s.length()-1;j++) {
String news = s.substring(0, j)+c+s.substring(j);
newRes.add(news);
}
}
res = newRes;
}
return res;
}
}
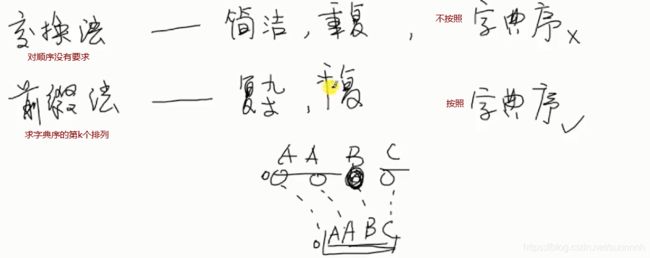
方法二:交换法。
import java.util.ArrayList;
public class Main {
static ArrayList list = new ArrayList();//存放结果
public static void main(String[] args) {
String str="ABC";
getPermutation2(str.toCharArray(),0);//方法二:对串str进行全排列
System.out.println(list);
}
/*
* 方法二:递归
* */
private static void getPermutation2(char[] str,int k) {
if(k==str.length) {//已确定完最后一个位置
list.add(new String(str));
return;
}
for(int i=k;i 方法三:前缀法。解决全排列中的字典序问题
找出“字典序”的第k个排列,我们需按照字典序(即从小到大)的顺序获取排列
需解决:(1)到第k个排列时,不再继续排列
(2)按照字典序递增
方法:每次从头开始扫描有序的数组[A B C],如果不在就加入
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
static int k; //字典序第k个排列
static int cnt=0;//记录当前已完成排列的数目
static ArrayList list = new ArrayList();//存放结果
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
k=sc.nextInt();//字典序第k个排列
String str="ABC";
getPermutation3("",str.toCharArray());//方法二:对串str进行全排列
System.out.println(list);
}
/*
* 方法三:前缀法
* 参数1prefix:当前的前缀
* 参数2a:全排列的数组
* (1)每次将未被加入前缀的字符加入 到当前的前缀prefix中
* (2)如果当前前缀的长度 = 数组a的长度。则排列完一次
* 且当前完成的排列是第k个,则结束
* */
private static void getPermutation3(String prefix,char[] a) {
int n = a.length;
//(1)判断是否完成一次排列
if(prefix.length()==n) {//已完成的一次排列
cnt++;
if(cnt==k) {//找到第k个排列
System.out.println(prefix);
System.exit(0);
}
}
//(2)依次向前缀加入字符
for(int i=0;i