【列车节能优化】--灰狼优化算法的应用
列车节能优化:灰狼优化算法的应用
-
- 一、研究背景
- 二、灰狼优化算法简介
- 三、灰狼优化算法在列车节能优化中的应用
-
- 1、算法求解模型
-
- 1.1 将多目标优化问题转化为单目标问题
- 1.2 基于Pareto原理求解
- 2、列车动力学模型
- 3、建立目标函数
- 4、决策变量的选取
- 四、仿真参数设置
- 五、部分源程序Matlab代码
- 六、部分实验结果仿真图
- 七、部分参考文献
一、研究背景
- 当今社会对能源资源的需求越来越大,如何提高列车的能效,减少能源的消耗和环境污染已经成为一个重要的研究方向。列车节能优化是一种综合运用机械、电气、控制等学科知识,通过采用先进的算法和技术手段来优化列车的能耗、运行效率和安全性,实现降低能源消耗和减少环境污染的目标。
列车节能优化的主要目的是在保证列车正常运行的前提下,最大限度地降低列车的能耗,从而达到节能的效果。具体来说,列车节能优化包括优化列车的运行策略、控制系统和车辆设计,如优化列车的牵引力、制动力、速度控制等,使列车在保证安全的情况下,最大限度地利用动能,减少能耗和环境污染。
二、灰狼优化算法简介
- 灰狼优化算法(Grey Wolf Optimizer,GWO)是一种新兴的优化算法,其灵感来源于狼群捕食行为。灰狼优化算法通过模拟狼群中的互动行为,寻找最优解。在列车节能优化中,我们可以将灰狼优化算法应用于调整列车速度等参数,实现节能的目的。
- 灰狼属于犬科动物,被认为是顶级的掠食者,它们处于生物圈食物链的顶端。灰狼大多喜欢群居,每个群体中平均有5-12只狼。特别令人感兴趣的是,它们具有非常严格的社会等级层次制度,如图1所示。金字塔第一层为种群中的领导者,称为 α \alpha α 。在狼群中 α \alpha α是具有管理能力的个体,主要负责关于狩猎、睡觉的时间和地方、食物分配等群体中各项决策的事务。金字塔第二层是 α \alpha α 的智囊团队,称为 β \beta β。 β \beta β 主要负责协助 α \alpha α 进行决策。当整个狼群的 α \alpha α 出现空缺时, β \beta β 将接替 α \alpha α 的位置。 β \beta β 在狼群中的支配权仅次于 α \alpha α,它将 α \alpha α 的命令下达给其他成员,并将其他成员的执行情况反馈给 α \alpha α 起着桥梁的作用。金字塔第三层是 δ \delta δ, δ \delta δ 听从 α \alpha α 和 β \beta β 的决策命令,主要负责侦查、放哨、看护等事务。适应度不好的 α \alpha α 和 β \beta β 也会降为 δ \delta δ。金字塔最底层是 ω \omega ω,主要负责种群内部关系的平衡。
- 此外,集体狩猎是灰狼的另一个迷人的社会行为。灰狼的社会等级在群体狩猎过程中发挥着重要的作用,捕食的过程在 α \alpha α的带领下完成。灰狼的狩猎包括以下 3个主要部分: 1)跟踪、追逐和接近猎物; 2)追捕、包围和骚扰猎物,直到它停止移动; 3)攻击猎物
三、灰狼优化算法在列车节能优化中的应用
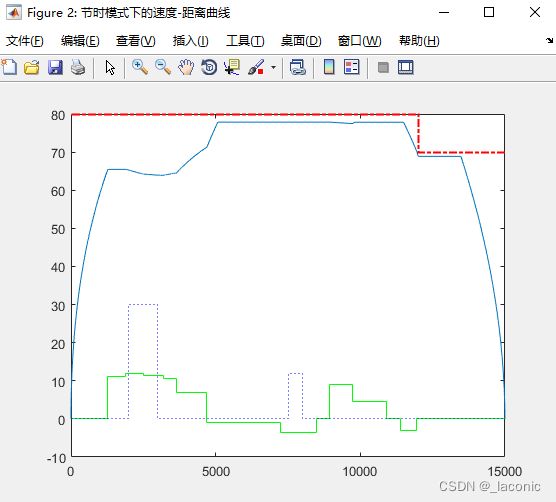
列车运行通常有两种操纵模式:节时模式和节能模式。其中节时模式是让列车以最短时间完成运行计划(即运行最大牵引力和最大制动力),该模式下要求列车贴近限制速度运行,当速度大于限制速度值后保持匀速运行,当速度小于限制速度值后牵引,即在运行过程中达到最高的技术速度。而节能模式是让列车选择最低能耗的优化操纵方案,使得列车在保证列车安全运行、准点的前提下,以比较节能的操纵方式完成运行计划。我们以节时模式和优化后的节能模式进行对比来证明灰狼优化算法优化后的能耗指标。
1、算法求解模型
对于多目标优化问题的求解,具有两种典型的思路:一种是化繁为简的求解思路,将其转化为求解单目标优化问题;一种是基于Pareto理论应用多目标优化的智能算法进行求解。
1.1 将多目标优化问题转化为单目标问题
将多目标优化问题转变为单目标优化问题进行求解的核心思想是通过一定的方式将各个子目标组装起来,组成一个包含多个子目标的数学表达式,这种求解方式对于多个目标通常有主次之分。以下具体介绍了几种常用的转化方法:
线性加权法。线性加权法是求解多目标优化问题的一种经典方法。该方法将多个优化目标函数分配一个固定的权重值 w i w_i wi,通过线性加权的方式将它们组合成一个新的综合目标函数。尽管这种方法将复杂的多目标问题简化成了单一的目标函数,但是由于多目标问题中各子优化目标及其评价指标存在差异,无法对权重系数的赋值确定统一合理的标准。因此,赋值权重大多需要根据求解者的主观判断,导致方法具有太强的主观操纵性。
主函数法。另一种将多目标优化问题转化为单目标优化问题的常用方法是主目标函数法。该方法选择一个主要的优化目标,将其他优化目标作为次要目标,并将其他目标的期望值大小转化为相应的约束条件,从而对优化变量的范围进行约束。这有助于优化过程向所期望的解的方向发展。通过这种方法,可以简化多目标优化问题的求解,但需要注意主要目标的选择和其他目标的转化方式,以确保所得到的单目标问题能够准确地反映出多目标优化问题的求解要求。
惩罚函数法。惩罚函数法是一种解决含有约束条件的最优化问题的常用方法。在惩罚函数法中,选定一个目标函数作为主要优化目标,将其他目标函数构造为惩罚函数,并将其作为约束条件添加到主目标函数中。这样就可以将含有约束条件的问题转化为一个无约束优化问题。由于列车运行优化控制问题通常含有较多的约束条件,惩罚函数法可以有效地将目标函数转换为无约束优化问题,从而减轻了主观赋权带来的不确定性和复杂性,并且可以方便地进行求解。因此,惩罚函数法在列车运行优化控制问题中具有广泛的应用前景。
1.2 基于Pareto原理求解
Pareto原理是多目标优化领域中的一种基本原理,也称为帕累托优化原理或帕累托最优解原理。其基本思想是:在多个优化目标存在的情况下,存在一组解集,其中任何一个目标函数值的改善都会导致另一个目标函数值的恶化,即不存在一种解能够同时使得所有目标函数达到最优值,而只有一些解具有“最优”的性质,这些解被称为帕累托最优解。
在多目标优化问题中,帕累托最优解具有以下两个特点:
非劣性:即帕累托最优解是在所有可行解中非劣的,不能被其他解支配。
多样性:即帕累托最优解集中的每一个解在目标函数值上都是独立的,没有一组解在所有目标函数上都优于其他解。
基于Pareto原理的求解方法被称为Pareto最优解求解方法,其主要目的是寻找一组非劣解,这些非劣解组成了帕累托最优解集合。通过Pareto最优解求解方法,我们可以在多目标优化问题中获得一些重要信息,比如理解目标之间的权衡,边界情况和最优解的多样性等。这对于决策制定和问题解决都有重要的指导意义。
2、列车动力学模型
- 在各类列车运动学模型当中,比较常见的有单质点、多质点以及质量带模型。就单质点模型而言,是把列车看做成一个质点,不会对车的长度和车厢彼此产生的耦合力进行考虑。在列车牵引计算研究中,由于该类模型并不复杂,因此得到了不少学者的应用;就多质点模型而言,多质点模型是将列车每个车厢都看成是一个质点,在列车的牵引计算中,考虑每个车厢的受力关系并求和得到列车的运动参数。该类模型由于需要对列车所具备的长度和列车车厢产生的受力加以考虑,故相比较于单质点模型,其更符合实际列车运行的状态。然而列车运行线路复杂且长,使用多质点模型可能会出现计算量大的问题,甚至在求取列车多目标速度曲线时会出现无解的情况。
单质点模型。所谓的单质点模型属于把整个列车当作一个质点看待,该点需要承受全部作用于列车之上的力,同时不会对车厢彼此产生的受力进行考虑。
多质点模型。就多质点模型而言,多质点模型是将所有的车厢都当做质点看待,这样设计的牵引计算模型可以考虑到列车长度带来的影响,可以将所有列车运行之间承受的合力真实反映出来。这样的模型仍然是通过受力分析来进行计算,但在受力分析的同时可以得到车辆之间所产生的拉力与推力,进而当列车到达变坡点抑或是变曲率点之际,就可产生渐变过程。由于多质点模型需对所有车辆具体情况进行考虑,相较于单质点模型而言,该模型实施具体计算较为复杂。
质量带模型。质量带模型的概念是将列车看做一个粗细均匀分配的木棒,列车按照其长度均匀分配质量。质量带模型比单质点模型多考虑了列车车厢的长度对于牵引计算的影响,在列车进入坡道或曲线时能精确利用变坡点或者变曲率点分段计算参数,与单质点模型相比减少了计算误差。与多质点模型相比,质量带模型不考虑车厢之间的推力或者拉力等受力关系,减少了计算量。 - 列车运行过程中受到牵引力 F F F、制动力 B B B、列车基本阻力 W W W和线路附加阻力 R R R的共同作用,假设列车质量为 M M M,列车运行时间 t t t,运行速度 v v v,运行距离 x x x,根据牛顿第二定律可推导得到列车运动的微分方程:
d x d t = v d v d t = F ( v ) − B ( v ) − W ( v ) − R ( x ) M (1) \begin{aligned} \frac{dx}{dt} \quad &=v \\ \frac{dv}{dt} \quad &=\frac{F(v)-B(v)-W(v)-R(x)}{M} \quad \end{aligned}\tag{1} dtdxdtdv=v=MF(v)−B(v)−W(v)−R(x)(1)
3、建立目标函数
- 在应用灰狼优化算法进行列车节能优化之前,我们需要建立一个目标函数。目标函数是用于评价列车行驶过程中的能量消耗的函数。
m i n Q = w 1 ∗ ∣ E − E 0 E 0 ∣ + w 2 ∗ ∣ T − T 0 T 0 ∣ \begin{align} min Q =& w_1*\lvert\frac{E-E_0}{E_0}\rvert+w_2*\lvert\frac{T-T_0}{T_0}\rvert \tag{2}\\ \end{align} minQ=w1∗∣E0E−E0∣+w2∗∣T0T−T0∣(2)式(2)中, Q Q Q为目标函数值, w 1 w_1 w1、 w 2 w_2 w2分别为运行能耗权重和运行时分权重, E E E为列车实际运行能耗, E 0 E_0 E0为列车期望的最小运行能耗,与线路条件和列车参数有关, T T T为列车实际运行时间, T 0 T_0 T0为区间给定计划运行时分。 - 同时,在列车节能优化中需满足某些约束条件。主要有速度限制约束、停车精度约束以及舒适度约束。
4、决策变量的选取
列车运行的过程中,司机的操纵简单说来就是在相应的位置对操纵工况进行调整。典型的列车操纵策略主要有节时操纵策略、节能操纵策略和混合操纵策略。针对列车不同的运行要求,应采用不同的操纵策略。无论采用哪种操纵策略,列车在启动加速阶段采用最大牵引力进行牵引加速,达到限速后,中间阶段根据运行要求采用合适的操纵策略。如果已知了列车运行过程中的操纵工况转换序列,以及相应的工况转换点位置,则列车运行曲线能够唯一确定。
工况转化序列可用如下公式描述:
P = ( p 0 , p 1 , p 2 , . . . , p i , . . . , p m ) \begin{align} P =& (p_0,p_1,p_2,...,p_i,...,p_m) \tag{3}\\ \end{align} P=(p0,p1,p2,...,pi,...,pm)(3)式(3)中, P P P为牵引、巡航、惰行和制动工况组成的工况转换序列,需满足工况转换约束。
基于工况序列表的列车列车节能操纵可描述为:预先给定列车运行过程中的操纵工况序列,将节能优化问题的解表示为求这些转换点的位置,即求解式(4)中的 X X X。
X = ( x 0 , x 1 , x 2 , . . . , x i , . . . , x m ) \begin{align} X=& (x_0,x_1,x_2,...,x_i,...,x_m) \tag{4}\\ \end{align} X=(x0,x1,x2,...,xi,...,xm)(4)式(4)中, x i x_i xi为工况切换点位置,且满足 0 = x 0 < x 1 < x 2 . . . < x i < . . . < x m < S 0=x_0
列车实际运行时,其工况转换次数是不定的,可采取若干个工况转换序列进行操纵。为提高节能操纵优化问题解的多样性,可预先给定多种操纵工况序列,比较各工况序列下的节能效果。假设现在操纵优化问题有两个合理的工况转换序列:
工况序列一: P 1 = ( p 0 , p 1 , p 2 , p 3 , p 4 , p 5 , p 6 , p 7 ) = ( 牵引 , 巡航 , 惰行 , 牵引 , 巡航 , 惰行 , 制动 ) P_1=(p_0,p_1,p_2,p_3,p_4,p_5,p_6,p_7)=(牵引,巡航,惰行,牵引,巡航,惰行,制动) P1=(p0,p1,p2,p3,p4,p5,p6,p7)=(牵引,巡航,惰行,牵引,巡航,惰行,制动)工况序列二: P 2 = ( p 0 , p 1 , p 2 , p 3 , p 4 , p 5 , p 6 , p 7 ) = ( 牵引 , 惰行 , 牵引 , 惰行 , 牵引 , 惰行 , 制动 ) P_2=(p_0,p_1,p_2,p_3,p_4,p_5,p_6,p_7)=(牵引,惰行,牵引,惰行,牵引,惰行,制动) P2=(p0,p1,p2,p3,p4,p5,p6,p7)=(牵引,惰行,牵引,惰行,牵引,惰行,制动)因此,仿真实验时则需分别求解其对应的工况转换点,比较两者得到节能操纵优化问题的最优解。实际应用时,工况序列可根据具体线路情况结合操纵经验预先给定。
四、仿真参数设置
以某实际线路为仿真线路,HXD1型电力机车牵引50节C80货车为仿真对象。货运列车基本属性如表1所示。
表1 货运列车的基本参数
| 参数 | 取值 |
|---|---|
| 列车编组 | 1机车+50货车 |
| 机车质量 | 200 ( t ) 200(t) 200(t) |
| 机车长度 | 35.22 ( m ) 35.22(m) 35.22(m) |
| 机车单位基本阻力 | 1.2 + 0.0065 v + 0.000279 v 2 ( N / t ) 1.2+0.0065v+0.000279v^2(N/t) 1.2+0.0065v+0.000279v2(N/t) |
| 货车质量 | 80 ( t ) 80(t) 80(t) |
| 机车长度 | 12 ( m ) 12(m) 12(m) |
| 货车单位基本阻力 | 0.92 + 0.0048 v + 0.000125 v 2 ( N / t ) 0.92+0.0048v+0.000125v^2(N/t) 0.92+0.0048v+0.000125v2(N/t) |
五、部分源程序Matlab代码
- HXD1型电力机车的牵引特性曲线
function f= TractionForce(vel)
% 根据牵引曲线计算列车牵引力大小
% 输入速度单位为m/s
f=0;
u=vel*3.6; %单位换算
if u<5
f=760;
elseif u<65
f=779-3.8*u;
elseif u<100
f=34560/u;
end
end
- HXD1型电力机车的制动特性曲线
function f= BrakingForce(vel)
% 根据制动曲线计算列车制动力大小
% 输入速度单位为m/s
f=0;
u=vel*3.6; %单位换算
if u<3
f=153.3*u ;
elseif u<=75
f=461;
elseif u<=100
f=34560/u;
end
end
- 列车运行时所受到的总阻力
function f = TotalResistance(vel,pos)
% 计算列车运行时所受到的总阻力
global RampArray;
global CurveArray;
global TrainLength;
global LocomotiveWeight TruckWeight TrainWeight;
%%
% tailStock=pos-TrainLength;
% bodyStock=pos-TRAINWGH/2;
% L=TrainLength;
u=vel*3.6;
%%
w0=1.2+0.0065*u+0.000279*u*u; %机车
w1=0.92+0.0048*u+0.000125*u*u; %C80货车
f1=w0*LocomotiveWeight*9.8/1000; %机车基本阻力
f2=w1*TruckWeight*9.8/1000;%货车基本阻力
f=0;
RampResistance=0;
CurveResistance=0;
n = size(RampArray, 2);
m = size(CurveArray, 2);
i=1;
j=1;
%% 列车坡道附加阻力计算公式,采用单质点模型
while (i<n)
if((pos>=RampArray(1,i)) && (pos<RampArray(1,i+1)))
wi = RampArray(2, i);
RampResistance =wi*TrainWeight*9.8/1000;
break;
end
i = i + 1;
end
%% 列车曲线附加阻力计算公式
while (j<m)
if pos>=CurveArray(1,j) && pos<CurveArray(1,j+1)
if 0==CurveArray(2,j)
wr=0;
CurveResistance =wr*TrainWeight*9.8/1000;
break;
else
wr=600/CurveArray(2,j);
CurveResistance =wr*TrainWeight*9.8/1000;
break;
end
end
j = j + 1;
end
%% 列车所受的总阻力
f=f1+f2+RampResistance+CurveResistance;
end
- 适应度函数设计
function fitness = CalculateFitness(Energy,Time)
% 计算适应度函数
% 定义全局变量
global Tmin;
% global Emax;
global Emin;
%% 适应度计算应该归一化
% 设置线性权重,包括能耗权重w1和时间权重w2
w1=0.5;
w2=0.5;
%% 分目标适应度值
f1=(abs(Energy-Emin))/Emin;
f2=(abs(Time-Tmin))/Tmin;
%% 适应度函数
fitness=w1*f1+w2*f2;
end
- 灰狼优化算法的主函数
function [bestFitnessPos,bestFitness,newPop,IterCurve]=GWO_main(option)
%灰狼化算法的主函数
global switchNumber;
global popSize iterNumber;
global upLimit lowLimit;
%灰狼优化算法参数
popSize=option.PopulationSize; %种群数量
iterNumber=option.MaxGenerations; %迭代次数
%% 产生初始种群
Population= InitializePopulation(popSize,switchNumber); %生成种群
%% 计算适应度值
for i=1:popSize
[~,Energy,Time,~]=ModelConstraint(Population(i,:),2);
fitness(i)=CalculateFitness(Energy,Time);
end
%% 对适应度排序,找到Alpha,Beta,Delta狼
%寻找适应度最小的位置
[SortFitness,indexSort] = sort(fitness);
%记录适应度值和位置
Alpha_pos = Population(indexSort(1),:);
Alpha_score = SortFitness(1);
Beta_pos = Population(indexSort(2),:);
Beta_score = SortFitness(2);
Delta_pos = Population(indexSort(3),:);
Delta_score = SortFitness(3);
gBest = Alpha_pos;
gBestFitness = Alpha_score;
%% 开始迭代
for iter=1:iterNumber
%% 把种群赋给旧种群
oldPopulation=Population;
a=2-iter*((2)/iterNumber);
%% 对个体进行评估
for i=1:popSize
for j=1:switchNumber
%% 根据Alpha狼更新位置
r1=rand(); % [0,1]随机数
r2=rand(); % [0,1]随机数
A1=2*a*r1-a; % 计算A1
C1=2*r2; % 计算C1
D_alpha=abs(C1*Alpha_pos(j)-Population(i,j)); % 计算距离Alpha的距离
X1=Alpha_pos(j)-A1*D_alpha; %位置更新
%% 根据Beta狼更新位置
r1=rand();%[0,1]随机数
r2=rand();%[0,1]随机数
A2=2*a*r1-a;% 计算A2
C2=2*r2; % 计算C2
D_beta=abs(C2*Beta_pos(j)-Population(i,j)); % 计算距离Beta的距离
X2=Beta_pos(j)-A2*D_beta; %位置更新
%% 根据Delta狼更新位置
r1=rand();%[0,1]随机数
r2=rand();%[0,1]随机数
A3=2*a*r1-a; % 计算A3
C3=2*r2; % 计算C3
D_delta=abs(C3*Delta_pos(j)-Population(i,j)); % 计算距离Delta的距离
X3=Delta_pos(j)-A3*D_delta; %位置更新
%更新位置
Population(i,j)=(X1+X2+X3)/3;
end
%% 边界检查
Population(i,:) = BoundaryCheck(Population(i,:),upLimit,lowLimit,switchNumber);
end
%% 判断个体是否符合约束条件
for i=1:popSize
[flag,Energy,Time,~]=ModelConstraint(Population(i,:),2);
if flag~= 0
Population(i,:)=lowLimit + (upLimit -lowLimit).*rand(1,switchNumber);
%再次测试
[flag,Energy,Time,~]=ModelConstraint(Population(i,:),2);
while flag~= 0
Population(i,:)=lowLimit + (upLimit -lowLimit).*rand(1,switchNumber);
[flag,Energy,Time,~]=ModelConstraint(Population(i,:),2);
end
end
fitness(i)=CalculateFitness(Energy,Time);
end
%% 合并新旧种群,取种群数量大小
newPopulation = [oldPopulation; Population];
% 计算适应度值
newfitness = zeros(size(newPopulation, 1), 1);
for i = 1:size(newPopulation, 1)
[~,Energy,Time,~] = ModelConstraint(newPopulation(i,:), 2);
newfitness(i) = CalculateFitness(Energy, Time);
end
% 排序并选择前setNum个个体
[~, sortIndex] = sort(newfitness, 'ascend');
newPopulation = newPopulation(sortIndex(1:popSize), :);
% 更新种群和适应度值
Population = newPopulation;
fitness = newfitness(sortIndex(1:popSize));
%% 更新适应度值
for i=1:size(Population,1)
% 更新 Alpha, Beta, Delta狼
if fitness(i)<Alpha_score
Alpha_score= fitness(i); % 更新alpha狼
Alpha_pos=Population(i,:);
end
if fitness(i)>Alpha_score && fitness(i)<Beta_score
Beta_score= fitness(i); % 更新beta狼
Beta_pos=Population(i,:);
end
if fitness(i)>Alpha_score && fitness(i)>Beta_score && fitness(i)<Delta_score
Delta_score= fitness(i); %更新delta狼
Delta_pos=Population(i,:);
end
end
%%
gBest = Alpha_pos;
gBestFitness = Alpha_score;
IterCurve(iter) = gBestFitness;
%% 显示迭代次数
disp(['第',num2str(iter),'次迭代']);
end
bestFitnessPos=gBest;
bestFitness=gBestFitness;
newPop=Population;
end
六、部分实验结果仿真图
- 节时模式下的速度-距离曲线
- 优化后的列车速度-距离曲线
- 优化后的工况序列
七、部分参考文献
[1] Mirjalili, Seyedali, Seyed Mohammad Mirjalili, and Andrew Lewis. “Grey wolf optimizer.” Advances in engineering software 69 (2014): 46-61.
[2] 杨彦强,刘海东,麻存瑞,徐靓.列车节能运行目标速度控制优化研究[J].交通运输系统工程与信息,2019,19(01):138-144.
[3] 张惠茹,贾利民,王莉.基于Pareto多目标优化的高速铁路列车节能驾驶曲线集生成[J].铁道学报,2021,43(03):85-91.
[4] 褚心童. 基于蚁群算法的城轨多列车节能运行优化研究[D].西南交通大学,2021.
[5] 杨杰. 货运列车节能运行优化与智能控制方法[D].北京交通大学,2017.
[6] 林轩. 货运电力机车节能优化操纵策略研究[D].西南交通大学,2018.