二叉搜索树，平衡二叉树，红黑树，B树，B+树

二叉树（BT）

树的一些基本概念：

• 层数：从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推
• 树的高度（深度）：树中结点的最大层次

注：节点的深度&高度
二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

两种特殊的二叉树：

1. 满二叉树

定义：只有度为0的结点和度为2的结点，并且度为0的结点在同一层上

如图：

2. 完全二叉树

定义：除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

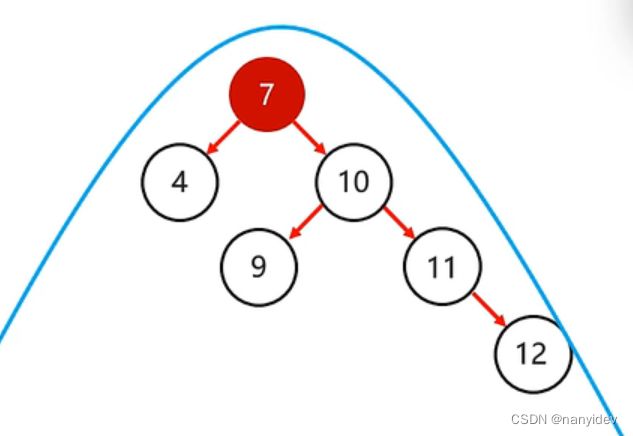
二叉搜索树（BST）

Binary Sort Tree，又称二叉查找树，二叉排序树，是一个有序树

满足以下条件：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

如图：

平衡二叉搜索树（AVL）

（注意，平衡二叉搜索树可简称为平衡二叉树，所以有的说法是平衡二叉树一定是二叉搜索树。但单独说平衡二叉树并没有要求是二叉搜索树。当然如果不是考试，死扣概念没有太大意义，所以平衡二叉树大多数情况都是二叉搜索树）

1. 定义

【由一个姓 AV 的大佬（G. M. Adelson-Velsky） 和一个姓 L 的大佬（ Evgenii Landis）提出。】

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树（即任意节点高度差不超过1）

如图：

2. 如何保持平衡——旋转

当我们在一个平衡二叉树上插入一个结点时，有可能会导致失衡，这时就需要旋转来平衡，那怎么旋转呢？

基本步骤（以左旋为例）：

第一步是确定支点：从添加的节点开始，不断的往父节点找不平衡的节点

第二步根据情况的不同

如果是下图情况：

• 以不平衡的点作为支点
• 把支点左旋降级，变成左子节点
• 晋升原来的右子节点

如果是下图情况：

• 以不平衡的点作为支点
• 将根节点的右侧往左拉
• 原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点

通常有四种情况

（1）LL：左左，当根节点的左子树的左子树有节点插入时—— 一次右旋

（2）LR：左右，当根节点的左子树的右子树有节点插入时—— 先局部左旋，再整体右旋

（3）RR：右右，当根节点的右子树的右子树有节点插入时—— 一次左旋

（4）RL：右左，当根节点的右子树的左子树有节点插入时—— 先局部右旋，再整体左旋

红黑树（RBTree）

1.定义

（1）一种自平衡的二叉搜索树
（2）不是高度平衡的
（3）特有的红黑规则（来维持平衡）

2.红黑规则

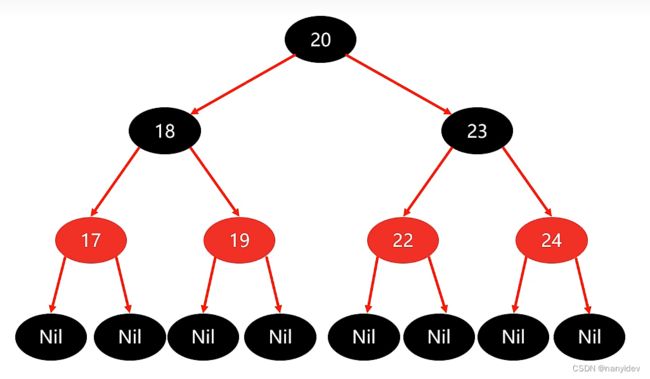
（1）每一个节点或是红色的，或者是黑色的

（2）根节点必须是黑色

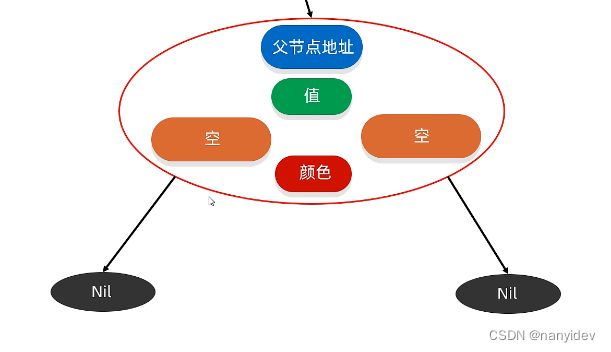
（3）如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nil，这些Nil视为叶节点，每个叶节点(Nil)是黑色的（注意这里的叶节点是空节点）

（4）如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)

（5）对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点

如图：

每一个节点的示意图如下（比正常的二叉树节点多了一个颜色）

3.插入规则

首先明确一点，红黑树在插入一个节点时，效率最高的是插入红节点（如果插入的节点是黑色，那么这个节点所在路径比其他路径多出一个黑色节点，这个调整起来会比较麻烦，如果是红色，就不影响）

所以以下默认插入节点是红色，再根据情况来调整

B树

1.定义

首先可以把B树看作一个M树，并且允许一个结点中包含多个key，并且满足下列条件：
（1）树中每个结点最多有M-1个key（有M个孩子节点），并且以升序排列

（2）若根节点不是叶子结点,则根结点至少有两个孩子结点

（3）除根节点外，其他结点至少有m/2个孩子结点

（4）所有叶子结点都在同一层上，即B树是所有结点的平衡因子均等于0的多路查找树。

（5）每个节点的结构是：

其中n表示key的数量，Pi 是指向孩子的指针，ki 是其中一个key的值

B树示意图如下：

一般可以简画成：

2.在磁盘系统中的应用

在我们的程序中，不可避免的需要通过IO操作文件，而我们的文件是存储在磁盘上的。计算机操作磁盘上的文件是通过文件系统进行操作的，在文件系统中就使用到了B树这种数据结构。

其实讲到B树和B+树都离不开磁盘系统

查找文件或者数据都需要索引（更快的查询）， 一般是通过 K:V（键值对）的形式，那么怎么设计一个文件系统的索引？（用什么样的数据结构）

如果设计的是线性形式，那查询效率肯定很低

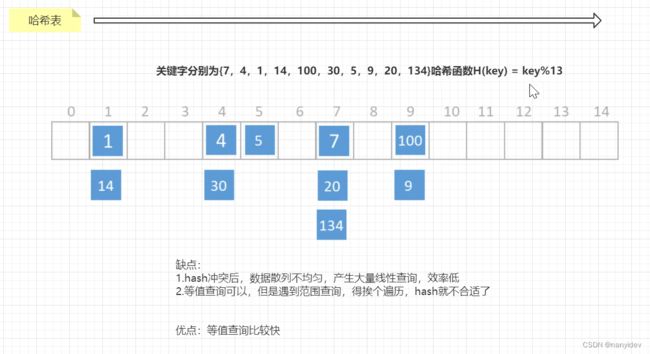
如果设计成哈希表，如下图，会出现哈希冲突也会产生大量线性查询

又考虑到二叉树，上面介绍了很多种二叉树，都还不够吗？

• 普通二叉树：数据无序，效率低
• BST二叉搜索树是有序的，但如果原始数据是有序的，则会退化为线性查找
• AVL平衡二叉树，当插入频率大于查找时，会消耗性能
• 红黑树：其实已经解决了上面几种的缺点，但是当数据量很大，查询次数就会增多（数据量大，树的深度就会不断增加）

所以才考虑到B树——多路平衡查找树

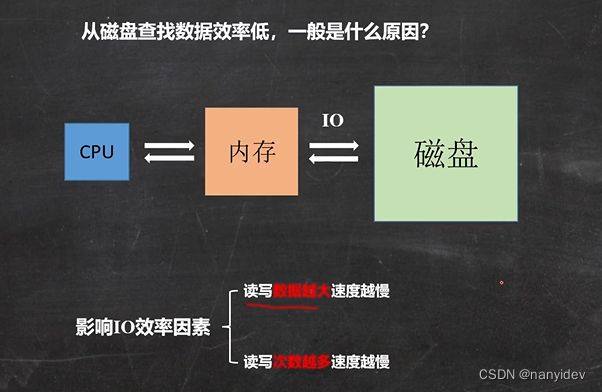
由于存储介质的特性，磁盘本身存取就比主存慢很多，为提高效率，要尽量减少磁盘I/O。 所以磁盘往往不是严格按需读取，而是每次都会预读——局部性原理。由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），因此预读可以提高I/O效率

内存和磁盘发生数据交互时，一般情况下有一个最小逻辑单元，称为页，页一般由操作系统决定多大，一般是4k或者8k，预读的长度一般为页的整倍数

文件系统的设计者利用了磁盘预读原理，将一个结点的大小设为等于一个页（1024个字节或其整数倍），这样每个结点只需要一次I/O就可以完全载入。那么3层的B树可以容纳102410241024差不多10亿个数据（如果换成二叉查找树，则需要30层）

B+树

1.定义

B+树是在B树的基础上又一次的改进（B树非叶子节点存储数据占用内存，因此进行改进）

B+树与B树的区别：

（1）非叶结点仅具有索引作用，也就是说，非叶子结点只存储key，不存储value

（2）树的所有叶结点构成一个有序链表，可以按照key排序的次序遍历全部数据。

其中Max Degree=3

2.应用

B+树的优点：
（1）由于B+树在非叶子结点上不包含真正的数据，只当做索引使用，因此在内存相同的情况下，能够存放更多的key。
（2）B+树的叶子结点都是相连的，因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。

参考链接：

https://www.bilibili.com/video/BV1rB4y1Q7e6/spm_id_from=333.788&vd_source=752a4cd440b20a1953dc8d254ef99696
https://www.bilibili.com/video/BV1iJ411E7xWp=135&vd_source=38cb30e60861b967d6cdfa51ce1c31fa