什么是强化学习(马尔可夫决策过程)
文章目录
-
- 什么是强化学习(马尔可夫决策过程)
-
- 1. 强化学习(概述)
- 2. 马尔可夫决策过程
-
- 2.1 马尔可夫假设
- 2.2 马尔可夫决策过程
- 2.3 状态值函数(state-value function)
- 2.4 状态-行动价值函数(action-valuefunction)
什么是强化学习(马尔可夫决策过程)
1. 强化学习(概述)
强化学习(Reinforcement learning,简称RL)是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。强化学习是除了监督学习和非监督学习之外的第三种基本的机器学习方法。与监督学习不同的是,强化学习不需要带标签的输入输出对,同时也无需对非最优解的精确地纠正。其关注点在于寻找探索(对未知领域的)和利用(对已有知识的)的平衡,强化学习中的“探索-利用”的交换,在多臂老虎机问题和有限MDP中研究得最多。
其灵感来源于心理学中的行为主义理论,即有机体如何在环境给予的奖励或惩罚的刺激下,逐步形成对刺激的预期,产生能获得最大利益的习惯性行为。这个方法具有普适性,因此在其他许多领域都有研究,例如博弈论、控制论、运筹学、信息论、仿真优化、多智能体系统、群体智能、统计学以及遗传算法。在运筹学和控制理论研究的语境下,强化学习被称作“近似动态规划”(approximate dynamic programming,ADP)。在最优控制理论中也有研究这个问题,虽然大部分的研究是关于最优解的存在和特性,并非是学习或者近似方面。在经济学和博弈论中,强化学习被用来解释在有限理性的条件下如何出现平衡。
强化学习有两个组成部分:环境和代理
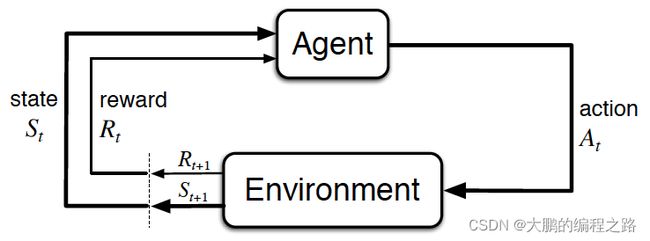
代理在特定环境中确定一个动作,而环境奖励该决定。这种奖励通常在采取若干行动后立即确定,而不是在采取行动后立即确定。这是因为,在许多情况下,当采取特定行动时,不可能立即评估该行动。
强化学习与前面讨论的深度学习密切相关。当一个代理决定一个行为并通过自己的学习作为环境的奖励时,就会使用主要由深度学习覆盖的人工神经网络。人工神经网络根据环境和代理的状态作为输入来判断行为,如果有奖励,则积极学习之前的输入值和行为。
2. 马尔可夫决策过程
2.1 马尔可夫假设
二十世纪初,数学家 Andrey Markov 研究了没有记忆的随机过程,称为马尔可夫链。这样的过程具有固定数量的状态,并且在每个步骤中随机地从一个状态演化到另一个状态。它从状态 S S S 演变为状态 S ′ S^{\prime} S′ 的概率是固定的,它只依赖于( S S S, S ′ S^{\prime} S′ ')对,而不是依赖于过去的状态(系统没有记忆)。
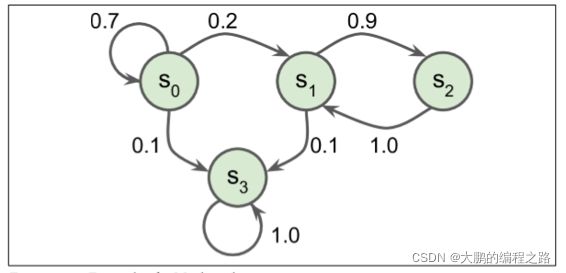
下 图 展示了一个具有四个状态的马尔可夫链的例子。假设该过程从状态S0开始,并且在下一步骤中有 70% 的概率保持在该状态不变中。最终,它必然离开那个状态,并且永远不会回来,因为没有其他状态回到S0。如果它进入状态 S 1 S_1 S1,那么它很可能会进入状态 S 2 S_2 S2(90% 的概率),然后立即回到状态 S 1 S_1 S1(以 100% 的概率)。它可以在这两个状态之间交替多次,但最终它会落入状态 S 3 S_3 S3 并永远留在那里(这是一个终端状态)。马尔可夫链可以有非常不同的应用,它们在热力学、化学、统计学等方面有着广泛的应用。
 马尔科夫假设的公式是
马尔科夫假设的公式是
P ( S t ∣ S 1 , S 2 , … , S t − 1 ) = P ( S t ∣ S t − 1 ) \mathbb{P}\left(S_{t} \mid S_{1}, S_{2}, \ldots, S_{t-1}\right)=\mathbb{P}\left(S_{t} \mid S_{t-1}\right) P(St∣S1,S2,…,St−1)=P(St∣St−1)在上面的公式中,坐标表示在某个时间点t上的状态 S t S_t St 受从最初状态 S 1 S_1 S1 到之前状态 S t S_t St 的影响。它清楚地描述了一系列连续存在且正在发生的状态,但实际上很难计算这些状态。因此,如果应用马尔科夫假设,即状态 S t S_t St 受前一状态 S t − 1 S_t-1 St−1 的影响最大,反映 S t − 1 S_{t-1} St−1 到 S t − 2 S_{t-2} St−2 的所有前一状态,则可以简化为上述公式的右变量。
2.2 马尔可夫决策过程
马尔可夫决策过程最初是在 20 世纪 50 年代由 Richard Bellman 描述的。它们类似于马尔可夫链,但有一个连结:在状态转移的每一步中,一个智能体可以选择几种可能的动作中的一个,并且转移概率取决于所选择的动作。此外,一些状态转移返回一些奖励(正或负),智能体的目标是找到一个策略,随着时间的推移将最大限度地提高奖励。
马尔可夫决策过程(Markov Decision Process, M D P MDP MDP)是基于马尔可夫过程的决策模型。MDP是状态(state)集 S S S、行为(action)集 A A A、状态转移概率(state transference概率)矩阵 P P P、补偿(response)函数 R R R、折扣因子 γ \gamma γ 配置。
M D P = ( S , A , P , R , γ ) M D P=(S, A, P, R, \gamma) MDP=(S,A,P,R,γ)状态集是 M D P MDP MDP 可以具有的所有状态集 S = S 1 、 S 2 . . . S t S={S _1、S_ 2... S_t} S=S1、S2...St 。如下所示,任何时刻的状态 S t S_ t St 都将成为状态集 S S S 中包含的特定状态。
S t = s , s ∈ S S_{t}=s, s \in S St=s,s∈S行为集是作为行为主体的Agent可以执行的所有行为的集合 A = a 1 、 a 2 、 … 、 a ∣ A ∣ A=a1、a2、…、a|A| A=a1、a2、…、a∣A∣ 。代理在某个时间点采取行动 A t = a , a ∈ A At=a,a∈A At=a,a∈A 。 M D P MDP MDP 中的状态转移概率比马尔可夫过程中的状态转移概率稍微复杂一些。 M D P MDP MDP 中的状态转移概率公式如下:
P s , s ′ a = P ( S t + 1 = s ′ ∣ S t = s , A t = a ) P_{s, s^{\prime}}^{a}=\mathbb{P}\left(S_{t+1}=s^{\prime} \mid S_{t}=s, A_{t}=a\right) Ps,s′a=P(St+1=s′∣St=s,At=a) P s , s ′ a P_{s, s^{\prime}}^{a} Ps,s′a 是当代理在某个状态下采取行为 a a a 时变为状态 s ′ s′ s′的概率。
补偿函数用于补偿代理在任何状态下所采取的行为。其公式如下:
R s a = E [ R t + 1 ∣ S t = s , A t = a ] R_{s}^{a}=\mathbb{E}\left[R_{t+1} \mid S_{t}=s, A_{t}=a\right] Rsa=E[Rt+1∣St=s,At=a]补偿函数返回在 R s a R_{s}^{a} Rsa 状态 s s s 中执行行为 a a a 时的补偿期望值。折扣因子是一个介于0和1之间的值,用于确定对过去行为的反映程度。折扣因素 γ \gamma γ 如果是1,则为<1、1、1、1和1,并为折扣因素 γ \gamma γ如果是0.9,则<1、0.9、0.81、0.729、0.6561>。也就是说,越是对遥远过去的补偿,越是削减并反映。
代理必须确定在任何状态下执行的行为 a a a ,称为策略(policy),策略 π π π 将朝着最大化总补偿的方向更新
π ( a ∣ s ) = P ( A t = a ∣ S t = s ) \pi(a \mid s)=\mathbb{P}\left(A_{t}=a \mid S_{t}=s\right) π(a∣s)=P(At=a∣St=s)
2.3 状态值函数(state-value function)
当代理执行一个动作时,它的状态会随着时间而改变。这时候,你会收到一份奖励,加上随时间打折的奖励所获得的价值可以表示如下:
V π ( s ) = E [ ∑ i = 0 γ i R t + i + 1 ∣ S t = s ] V_{\pi}(s)=\mathbb{E}\left[\sum_{i=0} \gamma^{i} R_{t+i+1} \mid S_{t}=s\right] Vπ(s)=E[i=0∑γiRt+i+1∣St=s]
策略 π π π 决定行为,决定的行为也决定状态。状态值函数返回当前状态 s s s 中遵循策略 π π π 时的值。
2.4 状态-行动价值函数(action-valuefunction)
状态-行为价值函数返回在任何状态下执行行为 a a a 时的价值。状态-行为价值函数也称为 Q v a l u e Q_{value} Qvalue。在任何状态 a a a 中执行行为a时获得的总奖励的期望值。
Q π ( s , a ) = E [ ∑ i = 0 γ i R t + i + 1 ∣ S t = s , A t = a ] Q_{\pi}(s, a)=\mathbb{E}\left[\sum_{i=0} \gamma^{i} R_{t+i+1} \mid S_{t}=s, A_{t}=a\right] Qπ(s,a)=E[i=0∑γiRt+i+1∣St=s,At=a]从公式可以看出,在状态值函数中为行为 a a a 添加了条件。状态-行为价值函数表示在当前状态 s s s 中沿策略 π π π 执行行为 a a a 时的价值。