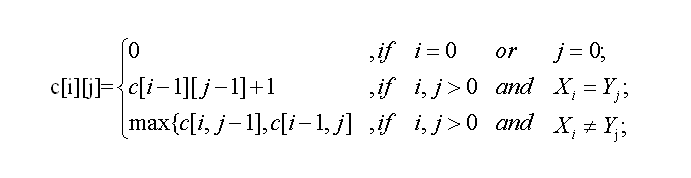最长公共子序列--动态规划(C++)
动态规划与分治方法类似,都是通过组合子问题来求解原问题。分治法将问题分为互不相交的子问题,递归的求解子问题,再将他们的解组合起来,求出原问题的解。相反的,动态规划用于子问题重叠的情况,即不同的子问题具有公共的子子问题(子子问题为将子问题分为更小的问题)。
1.简介
如果Z既是X的子序列,又是其它字符序列的子序列,而且Z是这些字符序列中最长的子序列,则称Z为这些字符序列的最长公共子序列(简称LCS)设计程序。
2.实现
子序列与子串不同,子串要求取连续的字符,而子序列不要求连续的字符,但必须按顺序取。
以两个字符串X
①穷举法:
穷举法,顾名思义,依次取X的子序列,Y的子序列来比较,而X的子序列有2 个,Y的子序列有 个,依次比较,这种算法的时间复杂度为O(2 * ),当m,n的数值比较大(即字符串X,Y较长)时,时间复杂度是非常大的。
②动态规划法:
将待求解的问题分解为若干个子问题,按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
对于求解X,Y两个字符串的最长公共子序列的问题,引入一个数组c[m][n],用c[i][j]记录字符串X[0]~X[i]与字符串Y[0]~Y[j]的LCS长度,引入一个数组b[m][n],用b[i][j]记录c[i][j]是由哪一个子问题求解得到的,填充’ ↑’,’← ’,’↖’。分别表示由上边、左边、左上的子问题求解得到。
矩阵的初始化:
数组c[m][n]初始化为0,然后按下边的公式填充c[m][n]矩阵
下面讨论时,字符串X,Y的下标从0开始,所以 c[i][j] 所对应的字符为 X[i-1] , Y[j-1].
当i,或j等于0的时候,c[i][j]=0意思为:
矩阵第一行和第一列为空出来的,不做字符的比较,全部填充为0;
当i,j>0时:
c[i][j]=c[i-1][j-1]+1 意思为:
当字符 X[i-1] = Y[j-1] 时,此时的LCS长度等于上一个子问题,即 X[i-1] 与 Y[j-1] 的LCS 长度加一;b[i][j]填 充为“ ↖”。
c[i][j]=max{ c[i,j-1],c[i-1,j] } 意思为:
当字符 X[i-1] ≠ Y[j-1] 时,此时的LCS长度等于前边的子问题取最优解,即 X[i-2] , Y[j-1] 与 X[i-1],Y[j-2] 的最大的LCS长度。b[i][j]填充“ ←”或“ ↑”。
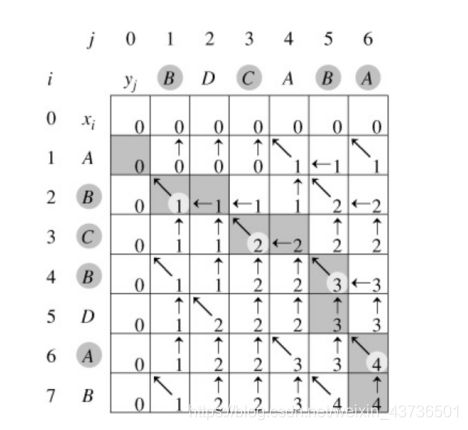
填充结束后,填充效果如下图,数组c[m][n]的值即为字符串X,Y的LCS长度。
输出最长公共子序列:
根据b[m][n]的方向回溯,当箭头方向为“↖”时,表示此处字符串X,Y所对应的字符相等,即可将其添加到temp字符串中,最后倒序输出即可,也可以利用递归函数回溯输出。
代码如下:
#include
using namespace std;
void LCS(string str1,string str2,int** &c,int** &b);
void print(string str1,int **b,int m,int n);
int main()
{
string str1,str2;
cin>>str1>>str2;
//两个矩阵,c存放LCS长度,b存放方向
//b的方向表示:1表示左侧,2表示上侧,3表示左上
int **c,**b;
LCS(str1,str2,c,b);
print(str2,b,str2.length(),str1.length());
}
//LCS函数
void LCS(string str1,string str2,int** &c,int** &b)//c,b传引用的目的是为了可以改变主函数中的数组
{
int len1 = str1.length(), len2 = str2.length();
//为c,b分配空间
c=new int*[len2+1];
b=new int*[len2+1];
for(int i=0;i=c[i][j-1]) //上边大 ,由上边的子问题得到
{
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else //由左侧的子问题得到
{
c[i][j]=c[i][j-1];
b[i][j]=1;
}
}
}
}
}
//回溯法输出LCS序列
void print(string str1,int **b,int m,int n)
{
if(m!=0&&n!=0)
{
if(b[m][n]==3)
{
//cout< 运行结果如下: