使用Pytorch从零开始构建Normalizing Flow

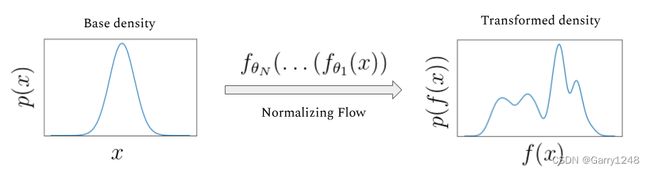
归一化流 (Normalizing Flow) （Rezende & Mohamed，2015）学习可逆映射 $f:X\to Z$, 在这里X是我们的数据分布，Z是选定的潜在分布。

归一化流是生成模型家族的一部分，其中包括变分自动编码器 (VAE) (Kingma & Welling, 2013)和生成对抗网络 (GAN) (Goodfellow 等人, 2014)。一旦我们学会了映射$f$，我们通过采样生成数据$z～p_Z$, 然后应用逆变换, $f^{-1}(z)=X_{Gen}$ 。

在本博客中，为了更好地理解归一化流，我们将介绍算法的理论并在 PyTorch 中实现流模型。但首先，让我们来看看归一化流的优点和缺点。

注意：如果您对生成模型之间的比较不感兴趣，您可以跳至“归一化流的工作原理”。

为什么要归一化流

有了 VAE 和 GAN 所显示的惊人结果，为什么要使用归一化流？我们列出了以下优点。(注：大部分优点来自 GLOW 论文（Kingma & Dhariwal，2018））

• NF 优化数据的精确对数似然，$log(p_X）$
  • VAE 优化下限 (ELBO)
  • GAN 学会欺骗鉴别器网络
• NF 推断精确的潜变量值z，这对于下游任务很有用。
  • VAE 推断潜变量值的分布
  • GAN 没有潜在分布
• 具有节省内存的潜力，NF 梯度计算按其深度恒定缩放。
  • VAE 和 GAN 的梯度计算都与其深度线性缩放
• NF 只需要一个编码器即可学习。
  • VAE 需要编码器和解码器网络
  • GAN 需要生成网络和判别网络

但请记住妈妈所说的话：“天下没有免费的午餐”。

归一化流的一些缺点如下：

• 可逆性和高效雅可比计算的要求限制了模型架构。
  • 稍后会详细介绍……
• 与其他生成模型相比，NF 的资源/研究较少。
  • 写这个博客的原因！
• NF 生成结果仍然落后于 VAE 和 GAN。

现在让我们深入了解一些理论！

归一化流如何工作

在本节中，我们简要回顾一下归一化流的核心。

变量的概率分布变化

考虑一个随机变量$X\in {\mathbb{R}}^d$ (我们的数据分布）和可逆变换$f:{\mathbb{R}}^d\mapsto {\mathbb{R}}^d$。
那么有一个随机变量$Z\in {\mathbb{R}}^d$ 是从$X$ 通过 $f$ 映射而来。
进一步的，
$$P(X=x)=P(f(X)=f(x))=P(Z=z)\text{\hspace{1em}(0)}$$
现在考虑一些X上的某个区间$\beta$，那么存在Z上一定的区间${\beta }^{\prime }$ 使得
$$P(X\in \beta )=P(Z\in {\beta }^{\prime })\text{\hspace{1em}(1)}$$
$${\int }_{\beta }{p}_{X}dx={\int }_{{\beta }^{\prime }}{p}_{Z}dz\text{\hspace{1em}(2)}$$
为了简单起见，我们考虑单个区域。
$$dx\cdot p_X(x)=dz\cdot p_Z(z)\text{\hspace{1em}(3)}$$
$$p_X(x)=\mid \frac{dz}{dx}\mid \cdot p_Z(z)\text{\hspace{1em}(4)}$$
注意：我们应用绝对值来保持相等，因为根据概率公理$p_X$和$p_Z$永远都是正的。
$$p_X(x)=\mid \frac{df(x)}{dx}\mid \cdot p_Z(f(x))\text{\hspace{1em}(5)}$$
$$p_X(x)=\mid det(\frac{df}{dx})\mid \cdot p_Z(f(x))\text{\hspace{1em}(6)}$$
注意：我们使用行列式来推广到多元情况($d>1$)
$$\log (p_X(x))=\log (\mid det(\frac{df}{dx})\mid )+\log (p_Z(f(x)))\text{\hspace{1em}(7)}$$
为我们的随机变量建模X，我们需要最大化等式（7）的右侧。
分解方程式：

• $\log (\mid det(\frac{df}{dx})\mid )$ 是拉伸/变化$f$的量
  适用于概率分布$p_X$
  • 此项是雅可比矩阵的对数行列式$\frac{df}{dx}$。我们将雅可比矩阵的行列式称为雅可比行列式。
• $\log (p_Z(f(x)))$ 限制$f$ 为将$x$转换到$p_Z$.

由于对Z没有任何限制，我们可以选择$p_Z$, 通常，我们选择$p_Z$为高斯分布。

单一功能并不能令我满意。我渴望更多。

顺序应用多个函数

我将向您展示如何顺序应用多个函数。
令$z_n$是顺序应用n个函数到$x\sim p_X$的结果。
$$z_n=f_n\circ \cdots \circ f_1(x)\text{\hspace{1em}(8)}$$
$$f=f_n\circ \cdots \circ f_1\text{\hspace{1em}(9)}$$
利用链式法则，我们可以用方程（8）修改方程（7）得到方程（10）, 如下。
$$\log (p_X(x))=\log (\mid det(\frac{df}{dx})\mid )+\log (p_Z(f(x)))\text{\hspace{1em}(7)}$$
$$\log (p_X(x))=\log (\prod _{i=1}^n\mid det(\frac{d{z}_i}{d{z}_{i-1}})\mid )+\log (p_Z(f(x)))\text{\hspace{1em}(10)}$$
其中，为了简洁，$x\triangleq z_0$
$$\log (p_X(x))=\sum _{i=1}^n\log (\mid det(\frac{d{z}_i}{d{z}_{i-1}})\mid )+\log (p_Z(f(x)))\text{\hspace{1em}(11)}$$
我们希望雅可比项易于计算，因为我们需要计算它n次。

为了有效计算雅可比行列式，函数$f_i$(对应$z_i$)被选择为具有下三角雅可比矩阵或上三角雅可比矩阵。由于三角矩阵的行列式是其对角线的乘积，因此很容易计算。

现在您已经了解了归一化流的一般理论，让我们来浏览一些 PyTorch 代码。

归一化流家族

在这篇文章中，我们将重点关注RealNVP（Dinh 等人，2016）。

尽管还有许多其他流函数，例如 NICE (Dinh et al., 2014)和 GLOW (Kingma & Dhariwal, 2018)。对于想要了解更多信息的同学，可以参考前面的博文。

RealNVP Flows

我们考虑单个 R-NVP 函数 $f:{\mathbb{R}}^d\to {\mathbb{R}}^d$, 其中输入 $\mathbf{x}\in {\mathbb{R}}^d$, 输出 $\mathbf{z}\in {\mathbb{R}}^d$。

快速回顾一下，为了优化我们的功能$f$ 以建模我们的数据分布 $p_X$, 我们想知道前向传递$f$，以及雅可比行列式$\mid det(\frac{df}{dx})\mid$

然后我们想知道函数的反函数$f^{-1}$, 所以我们可以转换采样的潜在值$z\sim p_Z$ 到我们的数据分布$p_X$,生成新样本！

前向传递

$$f(\mathbf{x})=\mathbf{z}\text{\hspace{1em}(12)}$$
前向传递是复制值同时拉伸和移动其他值的组合。首先我们选择一些任意值$ k$ (满足$0<k<d$) 分割我们的输入。
RealNVPs 前向传播如下:
$${\mathbf{z}}_{1:k}={\mathbf{x}}_{1:k}\text{\hspace{1em}(13)}$$
$${\mathbf{z}}_{k+1:d}={\mathbf{x}}_{k+1:d}\odot \exp (\sigma ({\mathbf{x}}_{1:k}))+\mu ({\mathbf{x}}_{1:k})\text{\hspace{1em}(14)}$$
这里 $\sigma ,\mu :{\mathbb{R}}^k\to {\mathbb{R}}^{d-k}$是任意函数。因此，我们会选择σ和μ两者都作为深度神经网络。下面是一个简单实现的 PyTorch 代码。

def forward(self, x):
    x1, x2 = x[:, :self.k], x[:, self.k:] 

    sig = self.sig_net(x1)
    mu = self.mu_net(x1)

    z1 = x1
    z2 = x2 * torch.exp(sig) + mu
    z = torch.cat([z1, z2], dim=-1)
    
    # log(p_Z(f(x)))
    log_pz = self.p_Z.log_prob(z)
    
    #...
view raw

对数雅可比行列式

该函数的雅可比行列式$\frac{df}{d\mathbf{x}}$:
$$\left[\begin{array}{cc}{I}_d& 0\\ \frac{d{z}_{k+1:d}}{d{\mathbf{x}}_{1:k}}& \text{diag}(\exp [\sigma ({\mathbf{x}}_{1:k})])\end{array}\right]\text{\hspace{1em}(15)}$$
雅可比矩阵的对数行列式将是:
$$\log (\det (\frac{df}{d\mathbf{x}}))=\log (\prod _{i=1}^{d-k}\mid \exp [{\sigma }_i({\mathbf{x}}_{1:k})]\mid )\text{\hspace{1em}(16)}$$
$$\log (\mid \det (\frac{df}{d\mathbf{x}})\mid )=\sum _{i=1}^{d-k}\log (\exp [{\sigma }_i({\mathbf{x}}_{1:k})])\text{\hspace{1em}(17)}$$
$$\log (\mid \det (\frac{df}{d\mathbf{x}})\mid )=\sum _{i=1}^{d-k}{\sigma }_i({\mathbf{x}}_{1:k})\text{\hspace{1em}(18)}$$

# single R-NVP calculation
def forward(x): 
  #...
  log_jacob = sig.sum(-1)
  #...
  
  return z, log_pz, log_jacob

# multiple sequential R-NVP calculation
def forward(self, x):
  log_jacobs = []
  z = x
  
  for rvnp in self.rvnps:
      z, log_pz, log_j = rvnp(z)
      log_jacobs.append(log_j)

  return z, log_pz, sum(log_jacobs)

反向

$$f^{-1}(\mathbf{z})=\mathbf{x}\text{\hspace{1em}(19)}$$
与其他流程相比，RealNVP 的优势之一是易于反转$\mathbf{F}$进入${\mathbf{F}}^{-1}$，我们使用等式 (14) 的前向传递将其表述如下:
$${\mathbf{x}}_{1:k}={\mathbf{z}}_{1:k}\text{\hspace{1em}(20)}$$
$${\mathbf{x}}_{k+1:d}=({\mathbf{z}}_{k+1:d}-\mu ({\mathbf{x}}_{1:k}))\odot \exp (-\sigma ({\mathbf{x}}_{1:k}))\text{\hspace{1em}(21)}$$
$$\iff {\mathbf{x}}_{k+1:d}=({\mathbf{z}}_{k+1:d}-\mu ({\mathbf{z}}_{1:k}))\odot \exp (-\sigma ({\mathbf{z}}_{1:k}))\text{\hspace{1em}(22)}$$

def inverse(self, z):
  z1, z2 = z[:, :self.k], z[:, self.k:] 
  
  sig = self.sig_net(z1)
  mu = self.mu_net(z1)
  
  x1 = z1
  x2 = (z2 - mu) * torch.exp(-sig)
  
  x = torch.cat([x1, x2], dim=-1)
  return x

小结

瞧，R-NVP 的配方完成了！

总而言之，我们现在知道如何计算$F(\mathbf{X})$, $\log (\mid \det (\frac{df}{d\mathbf{x}})\mid )$ 以及$f^{-1}(\mathbf{z})$。

下面是Github中完整的 jupyter 笔记本，其中包含用于模型优化和数据生成的 PyTorch 代码。

注意：在笔记本中，多层 R-NVP 在正向/反向传递之前翻转输入，以获得更具表现力的模型。

优化模型

$$\begin{gathered} \log (p_X(x))=\log (\mid det(\frac{df}{dx})\mid )+\log (p_Z(f(x))) \\ \log (p_X(x))=\sum _{i=1}^n\log (\mid det(\frac{d{z}_i}{d{z}_{i-1}})\mid )+\log (p_Z(f(x))) \end{gathered}$$

for _ in range(epochs):
  optim.zero_grad()
  
  # forward pass
  X = get_batch(data)
  z, log_pz, log_jacob = model(X)
  
  # maximize p_X(x) == minimize -p_X(x)
  loss = -(log_jacob + log_pz).mean()
  losses.append(loss)

  # backpropigate loss
  loss.backward()
  optim.step()

从模型生成数据

$$\begin{gathered} z\sim p_Z \\ {x}_{gen}=f^{-1}(z) \end{gathered}$$

# p_Z - gaussian
mu, cov = torch.zeros(2), torch.eye(2)
p_Z = MultivariateNormal(mu, cov)

# sample 3000 points (z ~ p_Z)
z = p_Z.rsample(sample_shape=(3000,))

# invert f^-1(z) = x
x_gen = model.inverse(z)

结论

总之，我们学习了如何使用可逆函数将数据分布建模为选定的潜在分布$f$。我们使用变量变化公式发现，为了对数据进行建模，我们必须最大化$f$的雅可比行列式，同时也约束$f$到我们的潜在分布。然后我们将这个概念扩展到顺序应用多个函数$f_n\circ \cdots \circ f_0$。最后，我们了解了RealNVP流程的理论和实现。