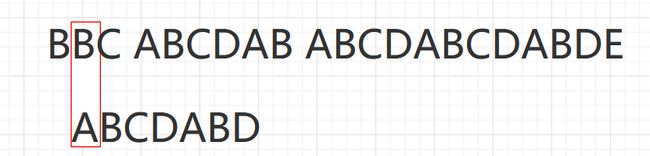数据结构与算法（Java）--常见算法

数据结构与算法（java)–链表

数据结构与算法（Java）–栈和递归

数据结构与算法（java)–排序算法及查找

数据结构与算法（java)–哈希表

数据结构与算法（Java）–数结构

数据结构与算法（Java）–图结构

数据结构与算法（Java）–常见算法

leetcode hot100

算法

1、分治算法

算法介绍

分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

基本步骤

分治法在每一层递归上都有三个步骤：

• 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
• 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
• 合并：将各个子问题的解合并为原问题的解

应用——汉诺塔

思路

A、B、C三个塔

• 如果只有一个盘，直接A->C

• 如果大于等于两个盘，就分成两部分。

  最下面的一个盘为一部分，上面的所有盘为一部分

  • 将上面部分的盘A->B
  • 最下面的盘A->C
  • 再将B中的盘B->C

实现代码

public class Demo1 {
   public static void main(String[] args) {
      hanoiTower(3, 'A', 'B', 'C');
   }

   /**
    * 汉诺塔
    *
    * @param num 盘的总数
    * @param a 第一个塔
    * @param b 第二个塔
    * @param c 第三个塔
    */
   public static void hanoiTower(int num, char a, char b, char c) {
      //如果只有一个盘，把这个盘从A移动到C
      if(num == 1) {
         System.out.println("把第" + num + "个盘从" + a + "->" + c);
         return;
      }
      //如果大于等于两个盘，将上面部分的盘从A借助C移动到B
      hanoiTower(num-1, a, c, b);
      //把最下面的盘从A移动到C
      System.out.println("把第" + num + "个盘从" + a + "->" + c);
      //把上面部分的盘从B借助A移动到C
      hanoiTower(num-1, b, a, c);
   }
} 

运行结果

把第1个盘从A->C
把第2个盘从A->B
把第1个盘从C->B
把第3个盘从A->C
把第1个盘从B->A
把第2个盘从B->C
把第1个盘从A->C 

博客推荐

在刷leetcode时有幸看到了一位大佬写的关于递归的博客，在此转载贴出。

点此跳转

2、动态规划

算法介绍

• 动态规划(Dynamic Programming)算法的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法
• 动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解
• 与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )
• 动态规划可以通过填表的方式来逐步推进，得到最优解

算法应用——01背包问题

物品	重量	价值
吉他	1	1500
音响	4	3000
电脑	3	2000

一个背包最多装4kg的东西，求

• 装入物品使得背包的总价值最大，且不超出背包的容量
• 要求装入的物品不能重复（01背包）

解题思路

算法的主要思想，利用动态规划来解决。每次遍历到的第 i个物品，根据 w[i]和 v[i]来确定是否需要将该物品放入背包中。即对于给定的 n个物品，设 v[i]、w[i]分别为第 i个物品的价值和重量，C为背包的容量。再令二维数组

v[i][j] 

表示在前 i个物品中能够装入容量为 j的背包中的最大价值。则我们有下面的结果

//表示填入表的第一行和第一列是 0，主要是为了方便表示物品和容量
(1) v[i][0]=v[0][j]=0; 

// 当准备加入新增的商品的重量大于当前背包的容量时，就直接使用上一个单元格的装入策略（装入物品的价值）
(2) 当 w[i]>j 时：v[i][j]=v[i-1][j] 

// 当准备加入的新增的商品的容量小于等于当前背包的容量,
// 装入的方式:
(3) 当 j>=w[i]时：v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}

v[i-1][j]：上一个装法的总价值

v[i] : 表示当前商品的价值

v[i-1][j-w[i]] ： 装入i-1商品，到剩余空间j-w[i]的总价值 

简单来说：

• 装入物品的容量大于背包容量时，直接使用之前装入背包物品的最大价值

• 装入物品容量小于等于背包容量时，比较

  • 装入该物品之前，背包物品的最大价值
  • 装入该后，该物品的价值+剩余容量能放入物品的最大价值

  选取较大者

实现代码

public class Demo2 {
   public static void main(String[] args) {
      //各个物品的重量
      int[] weight = {1, 4, 3};
      //各个物品的价值
      int[] value = {1500, 3000, 2000};
      //背包的最大容量
      int maxSize = 4;
      //各种方法的价值的最大值，第0行和第0列值为0，方便后续操作
      int[][] maxValue = new int[value.length+1][maxSize+1];
      //用于表示物品放入背包的方式
      int[][] method = new int[value.length+1][maxSize+1];

      //依次将物品放入背包
      for(int i = 1; i j) {
               maxValue[i][j] = maxValue[i-1][j];
            } else {
               //背包剩余的容量
               int remaining = j - weight[i-1];
               //如果放入该物品前的最大价值大于放入该物品后的最大价值，就不放入该物品
               if(maxValue[i-1][j] > value[i-1]+maxValue[i-1][remaining]) {
                  maxValue[i][j] = maxValue[i-1][j];
               } else {
                  maxValue[i][j] = value[i-1]+maxValue[i-1][remaining];
                  //存入放入方法
                  method[i][j] = 1;
               }
            }
         }
      }

      //打印放入背包的最大价值
      for(int[] arr : maxValue) {
         System.out.println(Arrays.toString(arr));
      }


      //打印价值最大的放法
      //存放方法的二维数组的最大下标，从最后开始搜索存放方法
      int i = method.length - 1;
      int j = method[0].length - 1;
      while(i > 0 && j > 0) {
         if(method[i][j] == 1) {
            System.out.println("将第" + i + "个物品放入背包");
            //背包剩余容量
            j -= weight[i-1];
         }
         i--;
      }
   }
} 

运行结果

[0, 0, 0, 0, 0]
[0, 1500, 1500, 1500, 1500]
[0, 1500, 1500, 1500, 3000]
[0, 1500, 1500, 2000, 3500]

将第3个物品放入背包
将第1个物品放入背包 

3、KMP算法

KMP是一个解决模式串在文本串是否出现过，如果出现过，找出最早出现的位置的经典算法

算法应用——字符串匹配

思路及图解

**问题：**有一个字符串 str1= BBC ABCDAB ABCDABCDABDE，和一个子串 str2=ABCDABD。现在要判断 str1 是否含有 str2, 如果存在，就返回第一次出现的位置, 如果没有，则返回-1

算法步骤

• 首先，用 str1的第一个字符和 str2的第一个字符去比较，不符合，关键词向后移动一位

[

• 重复第一步，还是不符合，再后移

[

• 一直重复，直到 Str1有一个字符与 Str2的第一个字符符合为止

[

• 接着比较字符串和搜索词的下一个字符，还是符合

[

• 遇到 Str1有一个字符与 Str2对应的字符不符合

[

重要步骤

• 这时候，想到的是继续遍历 str1的下一个字符，重复第 1步。(其实是很不明智的，因为此时 BCD已经比较过了，没有必要再做重复的工作，一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是”ABCDAB”

  • KMP 算法的想法是：设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，继续把它向后移，这样就提高了效率

• 怎么做到把刚刚重复的步骤省略掉？可以对 str2计算出一张部分匹配表，这张表的产生在后面介绍

  • str2的部分匹配表如下

    搜索词	A	B	C	D	A	B	D
    部分匹配值	0	0	0	0	1	2	0

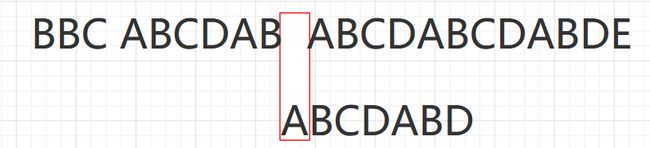
• 已知空格与 D不匹配时，前面六个字符”ABCDAB”是匹配的。查表可知，最后一个匹配字符B对应的部分匹配值为 2，因此按照下面的公式算出向后移动的位数：

  • 移动位数 = 已匹配的字符数 - 对应的部分匹配值
  • 因为 6 - 2 等于 4，所以将搜索词向后移动 4 位

[

[

• 因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为 2（”AB”），对应的部分匹配值为0。

  所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移 2 位

• 因为空格与 A不匹配，继续后移一位

• 逐位比较，直到发现 C与 D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动 4 位

[

• 逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动 7 位，这里就不再重复了

部分匹配表的生成

前缀与后缀

• 前缀：ABCD的前缀为[A, AB, ABC]
• 后缀：ABCD的后缀为[BCD, CD, D]

部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度。以”ABCDABD”为例，

• ”A”的前缀和后缀都为空集，共有元素的长度为 0；
• ”AB”的前缀为[A]，后缀为[B]，共有元素的长度为 0；
• ”ABC”的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度 0；
• ”ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为 0；
• ”ABCDA”的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为”A”，长度为 1；
• ”ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为”AB”，长度为 2；
• ”ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD,D]，共有元素的长度为 0。

实现代码

public class Demo3 {
   public static void main(String[] args) {
      String str1 = "BBC ABCDAB ABCDABCDABDE";
      String str2 = "ABCDABD";
		int result = getPosition(str1, str2);
		if(result != -1) {
			System.out.print("匹配位置是：str1[");
			System.out.println(result + "]");
		} else {
			System.out.println("匹配失败");
		}
   }

   /**
    *得到匹配字符串的部分匹配表
    *
    * @param matchStr 用于匹配的字符串
    * @return 部分匹配表
    */
   public static int[] getTable(String matchStr) {
      //部分匹配值的数组
      int[] sectionTable = new int[matchStr.length()];
      //匹配字符串的第一个元素没有前缀与后缀，部分匹配值为0
      sectionTable[0] = 0;
      //i用来指向部分匹配字符串末尾的字符，j用来指向开始的字符
      for(int i = 1, j = 0; i0且前缀后缀不匹配时，使用部分匹配表中前一个表项的值
         while (j > 0 && matchStr.charAt(j) != matchStr.charAt(i)) {
            j = sectionTable[j-1];
         }

         //如果前缀后缀匹配，j向后移，继续比较
         if(matchStr.charAt(j) == matchStr.charAt(i)) {
            j++;
         }
         //存入匹配值
         sectionTable[i] = j;
      }
      return sectionTable;
   }

   /**
    * 通过KMP算法匹配字符串，若匹配成功，返回第一个字符出现的位置
    *
    * @param str1 用于匹配的字符串
    * @param str2 要匹配的字符串
    * @return 第一个字符出现的位置，没有则返回-1
    */
   public static int getPosition(String str1, String str2) {
      //获得str2的部分匹配表
      int[] sectionTable = getTable(str2);
      for(int i = 0, j = 0; i < str1.length(); i++) {
         //两个字符匹配
         if(str1.charAt(i) == str2.charAt(j)) {
            j++;
            if(j == str2.length()) {
               //如果匹配完成，返回第一个字符出现位置
               return i - str2.length() + 1;
            }
         } else {
            //如果匹配失败了，使用部分匹配表，跳转到str1对应位置
            //如果j==0，说明没有字符被被匹配，直接让i指向str1的下一个字符
            if(j == 0) {
               continue;
            }
            //跳转步数 = 已经匹配的字符个数 - 部分匹配表对应的值
            int position = j - sectionTable[j-1];
            i += position;
            //因为循环后会+1，所以此处i-1
            i--;
            //重置j，重新匹配
            j = 0;
         }
      }
      return -1;
   }
} 

运行结果

匹配位置是：str1[15] 

4、贪心算法

算法简介

• 贪心算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优（即最有利)的选择，从而

希望能够导致结果是最好或者最优的算法

• 贪心算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果

算法应用——集合覆盖

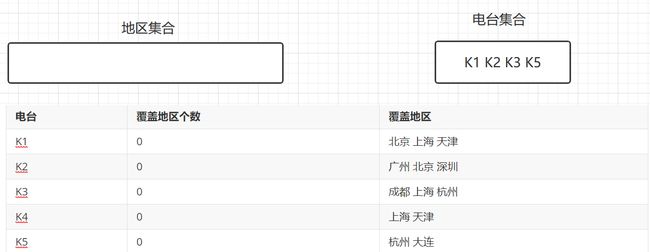
假设存在下面需要付费的广播台，以及广播台信号可以覆盖的地区。如何选择最少的广播台，让所有的地区都可以接收到信号

电台	覆盖地区个数	覆盖地区
K1	0	北京 上海 天津
K2	0	广州 北京 深圳
K3	0	成都 上海 杭州
K4	0	上海 天津
K5	0	杭州 大连

思路及图解

思路

• 遍历所有的广播电台, 找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区，但没有关系
• 将这个电台加入到一个集合中(比如 ArrayList), 想办法把该电台覆盖的地区在下次比较时去掉。
• 重复第 1步直到覆盖了全部的地区

图解

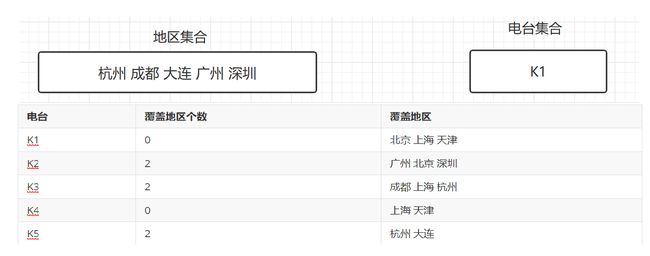
• 遍历电台的覆盖地区，发现K1覆盖的地区最多，将K1覆盖的地区从地区集合中移除。然后将K1放入电台集合中，并更新覆盖地区个数

• 遍历，发现K2覆盖的地区最多，将K2覆盖的地区从地区集合中移除。然后将K2放入电台集合中，并更新覆盖地区个数
  

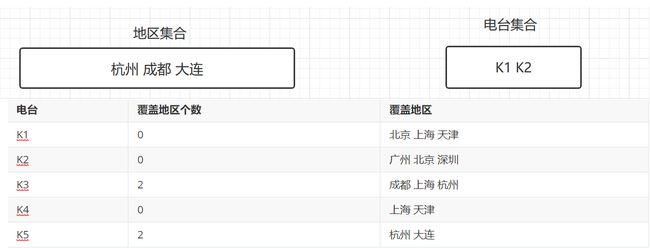
• 遍历，发现K3覆盖的地区最多，将K3覆盖的地区从地区集合中移除。然后将K3放入电台集合中，并更新覆盖地区个数

• 遍历，发现K5覆盖的地区最多，将K5覆盖的地区从地区集合中移除。然后将K5放入电台集合中，并更新覆盖地区个数。所有区域都被覆盖，算法结束

算法应用——钱币找零

假设纸币金额为1元、5元、10元、20元、50元、100元

要凑成123元应该尽可能兑换少的纸币

算法思路

• 尽可能从大面值一直往下减即可

实现代码

public class Demo1 {
   public static void main(String[] args) {
      splitChange(123);
   }

   /**
    * 拆分零钱
    *
    * @param money 钱币总金额
    */
   public static void splitChange(int money) {
      //零钱金额，纸币的种类
      int[] prices = {100, 50, 20, 10, 5, 1};
      //用于记录每种纸币的数量，下标与prices数组的下标对应
      int[] counts = new int[prices.length];
      //剩下的金额
      int surplus = money;
      if(money > 0) {
         //如果剩下的金额大于0
         while(surplus > 0) {
            //从大金额向小金额进行凑数
            for(int i = 0; i= 0) {
                  count++;
                  surplus -= prices[i];
               }
               counts[i] = count;
            }
         }
      }


      //打印结果
      System.out.println("凑成" + money +"元");
      for(int i = 0; i

运行结果

凑成123元
需要100元的纸币1张
需要20元的纸币1张
需要1元的纸币3张