UCAS - AI学院 - 自然语言处理专项课 - 第12讲 - 课程笔记

文本分类与聚类

文本分类

• 文本——领域信息分类

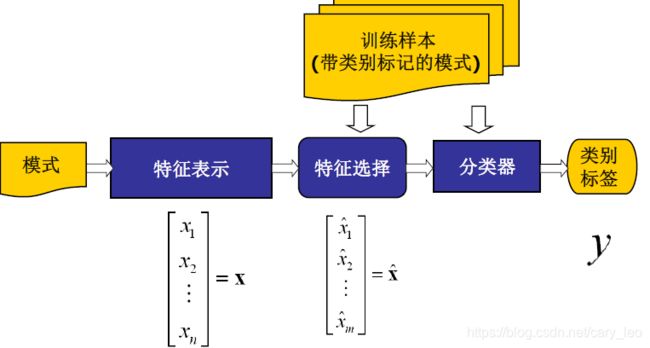
传统机器学习方法

• 文本表示

  • 向量空间模型——BoW模型
  • 词的权重
    • 词频TF
    • 布尔变量
    • 逆文档频率IDF
    • TF-IDF

• 特征选择

  • 文档频率：根据训练语料中的文档频率，对所有特征进行排序

  • 词频：根据训练语料中特征的频率，对所有特征进行排序

  • 基于无监督思想，特征选择缺乏类别信息的指导

  • 相关概率估计（文档数）

    

    • $P(c_j)\approx (A_{ij}+C_{ij})/N_{all}$
    • $P(t_i)\approx (A_{ij}+b_{ij})/N_{all}$
    • $P({\bar{t}}_i)\approx (C_{ij}+D_{ij})/N_{all}$
    • $P(c_j|t_i)\approx (A_{ij}+1)/(A_{ij}+B_{ij}+N_C)$
    • $P(c_j|{\bar{t}}_i)\approx (C_{ij}+1)/(C_{ij}+D_{ij}+N_C)$

  • 互信息

    • 关于两个随机变量互相依赖程度的一种度量
    • $I(X,Y)=H(X)-H(X|Y)={\sum }_x{\sum }_{y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$
    • $\mathrm{MI}(t_i,c_j)=\log \frac{P(t_i,c_j)}{P(t_i)P(c_j)}\approx \log \frac{A_{ij}{N}_{all}}{(A_{ij}+C_{ij})(A_{ij}+B_{ij})}$
    • ${\mathrm{MI}}_{avg}(t_i)={\sum }_{j=1}^{C}P(c_j)\mathrm{MI}(t_i,c_j)$

  • 信息增益

    • 衡量特征为分类系统带来多少信息
    • $\mathrm{IG}(t_i)=\left\{-{\sum }_j^{C}P(c_j)\log p(c_j)\right\}+\left\{P(t_i)\left[{\sum }_j^{c}P(c_j|t_i)\log P(c_j|t_i)\right]+P({\bar{t}}_i)\left[{\sum }_j^{c}P(c_j|{\bar{t}}_i)\log P(c_j|{\bar{t}}_i)\right]\right\}$
    • 信息增益可以通过互信息计算
    • $\mathrm{IG}(t_i)={\sum }_j^{C}P(t_i,c_j)\mathrm{MI}(t_i,c_j)+{\sum }_j^{C}P({\bar{t}}_i,c_j)\mathrm{MI}({\bar{t}}_i,c_j)$

  • ${\mathrm{X}}^2$统计量

    • 检验两个事件的独立性，度量了期望计数$E$与观察计数$N$之间的关系，越大越相关
    • ${\mathrm{X}}^2(t,c)={\sum }_{It}{\sum }_{Ic}\frac{(N_{It,Ic}-E_{It,Ic}{)}^2}{E_{It,Ic}}$
    • ${\mathrm{X}}^2(t,c)=\frac{N_{all}(A_{ij}{D}_{ij}-C_{ij}{B}_{ij}{)}^2}{(A_{ij}+C_{ij})(B_{ij}+D_{ij})(A_{ij}+B_{ij})(C_{ij}+D_{ij})}$
    • ${\mathrm{CHI}}_{avg}(t_i)={\sum }_{j}P(c_j){\mathrm{X}}^2(t_i,c_j)$

• 分类算法

  • 监督学习
    • 朴素贝叶斯
      • 假设：$P(X|c_j)\approx {\prod }_k^{N}P(w_k|c_j)\approx {\prod }_i^{M}P(w_i|c_j{)}^{N(w_i)}$
      • 决策规则：$P(c_j|x)\propto p(x,c_j)=P(c_j){\prod }_i^{M}P(w_i|c_j{)}^{N(w_i)}$
      • 最大似然估计：$P(c_j)\approx \frac{1+N(c_j)}{C+N_{all}}$，$P(w_i|c_j)\approx \frac{1+N(w_i,c_j)}{M+{\sum }_{i^{\prime }}N(w_{i^{\prime }},c_j)}$
    • 线性判别函数
      • $g(\mathbf{x})={\mathbf{w}}^{\top }\mathbf{x}+w_0={\sum }_{l=1}^M{w}_l{x}_l+w_0$
      • 不同的优化准则决定的不同的线性判别面
      • 优化——随机梯度下降
    • 支持向量机
      • 最大间隔优化$y={\mathbf{w}}^{\top }\mathbf{x}+b$
      • 优化准则$\min \frac{1}{2}\Vert \mathbf{w}{\Vert }^2,\text{s.t.}{y}_i({\mathbf{w}}^{\top }{\mathbf{x}}_i+b)\ge 1,i=1,\dots ,n$
    • 最大熵模型
  • 无监督、半监督学习

深度学习方法

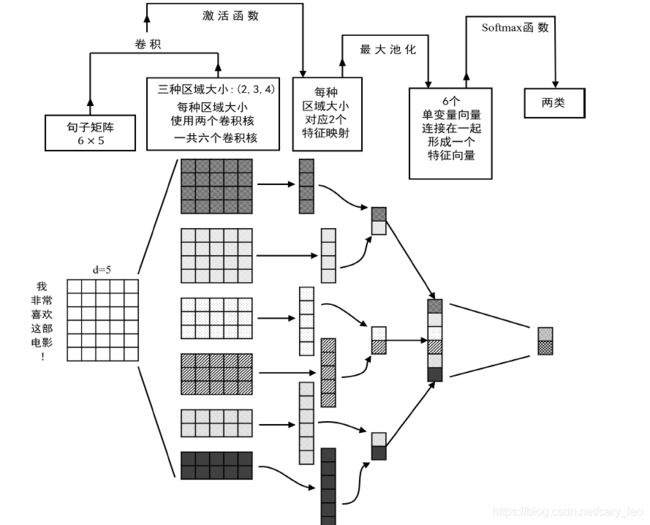
• 基于CNN的方法

  

  • 文本视为词序列，每个词用词向量表示
  • 文本按词窗口卷积（一维向量特定个词卷积）$y_i^t=F_t(W{x}_{i:i+h-1}+b)$
  • 多个卷积结果最大池化${\hat{y}}^t=\max (y_i^t)$
  • 不同词窗口卷积结果构造最终分类向量

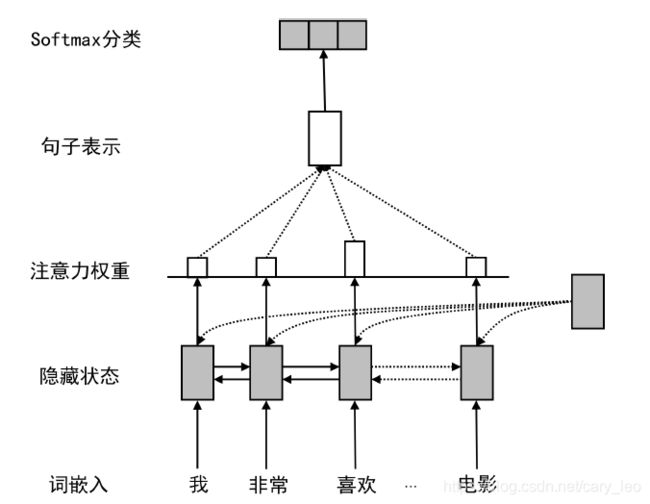
• 基于循环神经网络的方法

  

  • RNN+注意力机制

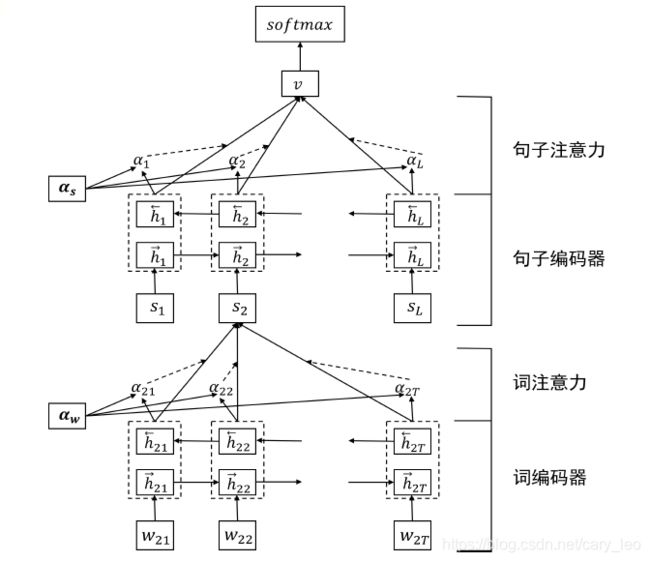
• 基于层次化网络的方法

  

  • 文本看作句子的序列
  • 句子看作词的序列
  • 层次化处理得到文本表示

文本分类性能评估

• 分类效果评估
  • TP、TN、FP、FN
  • 召回率、精确率、F-1值
  • 正确率、宏平均（少类）、微平均（多类）
  • 二分类且类别互斥的情况下，微观平均准确率、召回率和F1值均相同
  • P-R曲线、ROC曲线

文本聚类

文本相似度度量

• 两个文本对象之间的相似度
  • 基于距离的度量
    • 欧式距离
    • 曼哈顿距离
    • 切比雪夫距离$d(a,b)={\max }_k|a_k-b_k|$
    • 闵可夫斯基距离$d(a,b)={\left({\sum }_{k=1}^M(a_k-b_k{)}^p\right)}^{1/p}$
  • 基于余弦的度量
    • $\cos (a,b)=\frac{a^{\top }b}{\Vert a\Vert \Vert b\Vert }$
  • 杰卡德相似系数
    • $\mathrm{Jaccard}=\frac{|a\cap b|}{|a\cup b|}$
  • 基于分布的度量
    • $D_{KL}(P||Q)={\sum }_{i}P(i)\log \frac{P(i)}{Q(i)}$
    • 对称化处理$D_{SKL}=D_{KL}(P||Q)+D_{K}LQ||P$
• 两个文本集合之间的相似度
  • 最短距离法
  • 最长距离法
  • 簇平均法
  • 重心法（各自重心之间的距离）
  • 离差平方和法
    • 两个簇中格言本到两个簇合并后的簇中心的距离平方和，相比于各样本到各自簇中心之间的距离平方和增量
    • $d(C_m,C_n)={\sum }_{x^{(k)}\in C_m\cup C_n}d(x^{(k)},\bar{x}(C_M\cup C_n))-{\sum }_{x^{(i)}\in C_m}d(x^{(i)},\bar{x}(C_m))-{\sum }_{x^{(j)}\in C_n}d(x^{(j)},\bar{x}(C_m))$
• 文本对象和文本集合的相似性
  • 样本与簇之间的相似性通常转化为样本间的相似度或簇间的相似度进行计算
  • 如果用均值向量来表示一个簇，那么样本与簇之间的相似性可以转化为样本与均值向量的样本相似性
  • 如果将一个样本视为一个簇，那么就可以采用前面介绍的簇间的相似性度量方法进行计算

文本聚类算法

• K-means聚类
  • 簇内平方和法
  • 词频作为特征
  • 文本降维后进行聚类
  • Pros：理解简单、易于实现、应用广泛
  • Cons：聚类数难确定、中心点选择需要技巧、距离函数选择没有确定准则
• 单遍聚类
  • 遍历一遍即可完成聚类
  • 初始化：读入一个文本，作为一个簇
  • 逐个读入文本，相似度小于阈值，产生一个新的簇，否则归类到最大相似度的簇
• 层次聚类
  • 依据一种层次架构将数据逐层进行聚合或分裂，最终将数据对象组织成聚类树状的结构
  • 自底向上的聚合式层次聚类
  • 自顶向下的分裂式层次聚类
  • 分裂式需要注意的问题
    • 选择哪个类进行分裂
    • 具体的分裂策略
• 密度聚类
  • 样本空间中分布密集的样本点被分布稀疏的样本点分割
  • DBSCAN算法相关概念
    • 邻域半径$r$
    • 高密度区域形成的最小样本数$x$
    • $r$邻域：某样本$P$的$r$邻域指以$p$为中心、$r$为半径形成圆形领域
    • 核心样本：如果某点$P$的$r$邻域中的样本数不少于$n$，则称$P$为核心样本
    • 密度直达：如果样本$Q$在核心样本$P$的$r$邻域内，则称$Q$从$P$密度直达
    • 密度可达：如果存在一个样本序列$P_1,\dots ,P_T$，且对任意$t=1,\dots ,T-1$，$P_{t+1}$可由$P_t$密度直达，则称$P_T$从$P_1$密度可达，序列中的传递样本$P_2,\dots ,P_{T-1}$均为核心样本
    • 密度相连：如果存在核心样本$P$，使得样本$Q_1$和$Q_2$均从$P$密度可达，则称$Q_1$和$Q_2$密度相连
  • DBSCAN算法认为，对于任一核心样本$P$，样本集中所有从$P$密度可达的样本构成的集合属于同一个聚类
  • DBSCAN算法
    • 从某个核心样本出发，不断向密度可达的区域扩张，从而得到一个包含核心样本和边界样本的最大区域，该区域中任意两点密度相连，聚合为一个簇
    • 继续寻找未被标记的核心样本，重复上述过程，直到样本集中无新核心样本为止
    • 样本集中未包含在任何簇中的样本点构成噪声点簇

文本聚类性能评估

• 外部标准
  • 通过测量聚类结果与参考标准的一致性评价聚类结果的优劣
    • 参考标准通常由专家构建或人工标注获得
    • 聚类标准$\mathcal{P}=\{P_1,\dots ,P_m\}$
    • 聚类结果$\mathcal{C}=\{C_1,\dots ,C_k\}$
    • 对于数据集$D$中两个不同样本$d_i$和$d_j$，其隶属于$\mathcal{C}$和$\mathcal{P}$的情况，定义四种关系
      • SS：二者在结果中属于同簇，标准中也属于同簇——a
      • SD：二者在结果中属于同簇，标准中属于不同簇——b
      • DS：二者在结果中属于不同簇，标准中属于同簇——c
      • DD：二者在结果中属不同簇，标准中也属不同簇——d
    • Rand统计量：$RS=\frac{a+d}{a+b+c+d}$
    • Jaccard系数：$JC=\frac{a}{a+b+c}$
    • FM指数：$FMI=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}$
    • 主要考察聚类宏观性能，在传统的聚类有效性分析中被较多地使用，在文本聚类研究中并不多见
  • 微观指标
    • 精准率$P(P_j,C_i)=\frac{|P_j\cap C_i|}{|C_i|}$
    • 召回率$R(P_j,C_i)=\frac{|P_j\cap C_i|}{|P_j|}$
    • F-1值$F_1(P_j,C_i)=\frac{2P(P_j,C_i)R(P_j{C}_i)}{P(P_j,C_i)+R(P_j,C_i)}$
    • 宏观F-1值：$F_1(P_j)={\max }_i{F}_1(P_j,C_i),F_1=\frac{{\sum }_j|P_j|F_1(P_j)}{{\sum }_j|P_j|}$
    • 更加丰富地刻画了各簇聚类结果与聚类参考标准之间的吻合度
• 内部标准
  • 基于内部标准的聚类性能评价方法不依赖于外部标注，而仅靠考察聚类本身的分布结构评估聚类的性能
  • 簇间最大，簇内最小
  • 常用方法：轮廓系数
  • $d$所在簇未$C_m$，$a(d)$为其于簇中其他样本的平均距离，$b(d)$为其于其他簇中样本的最小平均距离
  • 样本$d$的轮廓系数$SC(d)=\frac{b(d)-a(d)}{\max a(d,b(d))}$
  • 总体轮廓系数$SC=\frac{1}{N}{\sum }_{i=1}^{N}SC(d_i)$
  • 系数越大，聚类效果越好