详细解答T-SNE程序中from sklearn.manifold import TSNE的数据设置，包括输入数据，绘制颜色的参数设置，代码复制可用！！

---

前言——TSNE是t-Distributed Stochastic Neighbor Embedding的缩写

TSNE是t-Distributed Stochastic Neighbor Embedding的缩写,它是一个非线性降维算法。

TSNE的主要作用和优点如下:

• 将高维数据投影到低维空间,如二维或三维,实现高维数据的可视化。

• 相比其他降维方法如PCA,TSNE在保留局部结构信息上的效果更好,尤其适用于高维稠密数据。

• 它可以很好地区分数据中的簇结构,有利于观察不同类别或类型的数据分布情况。

1、可运行的T-SNE程序

from sklearn.datasets import load_iris
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TkAgg')

# 加载数据
iris = load_iris()
X = iris.data
y = iris.target

# TSNE降维
tsne = TSNE(n_components=2, random_state=0)
X_tsne = tsne.fit_transform(X)

# 绘制点
plt.scatter(X_tsne[:,0], X_tsne[:,1], c=y, marker='o', s=5)

# 添加图例
plt.legend(iris.target_names)

# 添加标题
plt.title("TSNE projection of the Iris dataset")

plt.show()

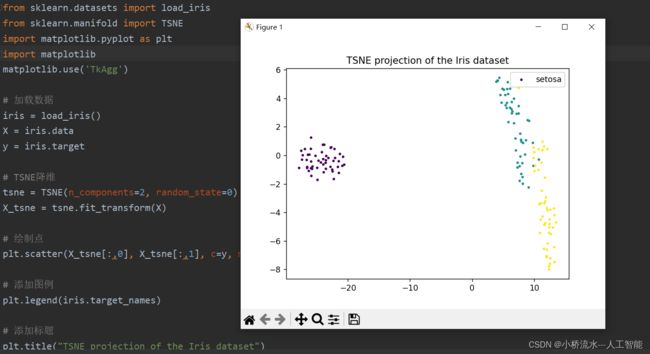
2. 实验结果

3、针对上述程序我们详细分析T-SNE的使用方法

3.1 加载数据

• load_iris()函数从sklearn.datasets模块加载鸢尾花数据集,
• iris包含数据集的特征数据X和标签数据y。

3.2 TSNE降维

• TSNE是一种非线性降维算法,用于高维数据的可视化。它可以将高维数据投影到二维或三维空间。

• TSNE(n_components=2)实例化一个TSNE模型,降维后的维度数设为2。

• random_state=0固定随机数种子,使得结果可重复。

• fit_transform(X)对特征数据X进行降维,返回降维后的新特征X_tsne。

3.3 绘制点

• X_tsne包含每个样本的二维坐标。

• plt.scatter以(x,y)坐标方式绘制每个点,c=y指定点的颜色。

• marker='o’设置点的形状为圆形。

• s=5控制点的大小。

通过TSNE降维,高维数据X被投影到二维空间,得到低维表示X_tsne。然后根据X_tsne和y进行散点图绘制,就可以实现TSNE降维结果的可视化。这是TSNE的标准流程。

3.4 关于颜色设置，颜色使用的标签数据的说明c=y

c=y这行代码的含义和作用是:

• c参数用于设置散点图中每个点的颜色。

• y变量包含了样本的类别标签信息。对于鸢尾花数据集来说,y取值为0、1或2,分别表示三种花的类别。

• 当我们设置c=y时,就是根据每个样本在y中的类别标签值,来动态设置这个样本点在散点图中的颜色。

• 具体来说:

  • 如果一个样本的y值为0,那么这个点的颜色就会取颜色映射中的第一个颜色。

  • 如果y值为1,点颜色取第二个颜色。

  • 如果y值为2,点颜色取第三个颜色。

• 这样每个类别的样本点就会使用不同的颜色来绘制,从而在可视化结果中清晰区分开各个类别。

---

总结

• 在科研中,TSNE广泛应用于图像分类、自然语言处理等领域的数据降维和可视化。

• 比如对神经网络分类结果进行TSNE降维,可以观察不同类别样本在特征空间中的分布,有助于分析模型表现。

• 对文本语料进行TSNE降维,可以观察词汇在语义空间中的分布,帮助理解语义结构。

• 对单细胞RNA-seq数据进行TSNE降维,可以观察不同类型细胞在表达空间中的分布,有助于发现新型细胞亚群。

所以总体来说,TSNE通过高效的降维和保留局部结构,有助于科研人员直观观察高维数据的内在结构,分析模型效果,发现数据中的新知识,从而推动科研工作的进展。它为数据可视化和理解提供了重要的工具支持。