计算机视觉算法——基于Transformer的目标检测（Efficient DETR / Anchor DETR / Conditional DETR / DAB DETR）

计算机视觉算法——基于Transformer的目标检测（Efficient DETR / Anchor DETR / Conditional DETR / DAB DETR）

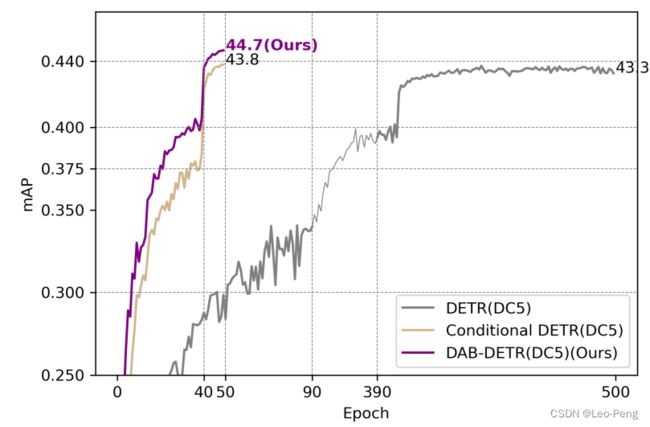
自DETR年提出来之后，许多Paper针对DETR中收敛速度慢、检测效果差等问题进行了针对性优化，在
计算机视觉算法——基于Transformer的目标检测（DETR / Deformable DETR / Dynamic DETR / DETR 3D）中我们对DETR以及其部分优化方法进行了总结，本篇博客我们针对这些优化方法进行进一步补充。

1. Efficient DETR

Efficient DETR发表于2021年CVPR，该论文主要研究思路是期望Query能够被更好地初始化进而网络可以被加速收敛。文章主体的思路是循序渐进、由浅入深的，下面我们按照文章原本的思路来介绍该方法。

1.1 Impact of Initialization of Object Queries

首先文章提到，在DETR的中有，会发现Decoder的层数会比Encoder的层数更加重要，如下图所示：

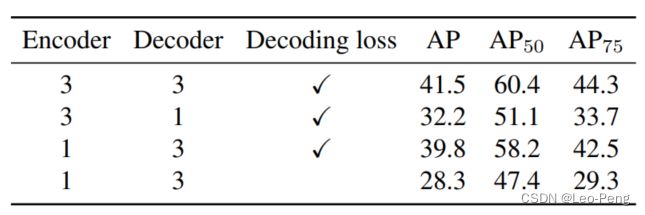
将Encoder层数从3层减到1层，AP仅掉了1.7个点，但是将Decoder从3层见到1层，AP掉了将近10个点。那么为什么DETR的结果会对Decoder层数这么敏感呢？文章指出，最终检测结果是从Object Query中获得的，而Object Query是被随机初始化并在Decoder的每一层迭代中逐渐被更新，因此当Decoder层数减少时，Object Query收敛不充分，网络性能也会随之下降。

除此之外，作者还发现在DETR中的Object Query通过学习后会专注于图像中的某一个特殊区域，因此研究Object Query到图像空间的映射能够帮助我们去理解Object Query是如何在Decoder的一层层迭代中逐步收敛的。在Deformable DETR中，Decoder部分正好做了这么一件事情，Defomable DETR的Decoder会从Query中通过一个MLP生成Reference Point。因此作者可视化了Deformable DETR中的Reference Point收敛前和收敛后的变化情况如下：

并且还对比了不同的初始化Refeence Point在收敛后的分布趋近于是相同的：

因此作者得出结论：在的Decoder中，只要堆叠的层数足够多，迭代时间足够长，不同的初始化Object Query都能收敛到相似的状态。因此文章的研究目标就变成了，我们如何通过尽可能少的Decoder层数，尽可能少的迭代次数使得网络达到同样好的效果。就此作者提出了Efficient Net，网络结构如下：

1.2 Dense and Sparse Part

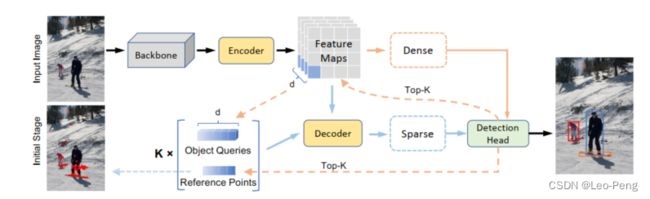
网络先通过ResNet提取多尺度特征，然后Defomable Encoder得到Feature Maps，其中Dense部分是就是在Feature Map上直接接一个Detection Head，Detection Head包括Classification Branch和Regression Branch，其中Classification为一层MLP用于获取类别，Regression Branch为三层MLP用于获取Anchor的4个回归参数，Feature Maps通过Dense部分会给每个特征像素都输出若干Anchor。

对于Dense部分输出的Anchor，Sparse部分会选取得分最高的前K个。其中：

1. Anchor的几何信息作为Reference Points的初始位置；
2. Anchor对应的Feature Maps上的256维Feature作为Object Query的初始值；
3. Sparse部分和Dense部分共用同一个Detection Head**。

这三点都可以帮助Sparse 部分更快地收敛，最后网络输出的结果是从Sparse部分输出的结果中获得的。还有一个训练技巧时，在训练初期，由于Dense部分并不能很好地对Feature Maps进行预测，因此Sparse部分会选取300个Proposal的Object Query，而随着训练逐渐收敛，会线性地将Object Query降到100个。

在最后的结果中，Efficient Net仅使用了三层Deformable Encoder和一层Deformable Decoder就使得性能超过了原始六层的Deformable DETR：

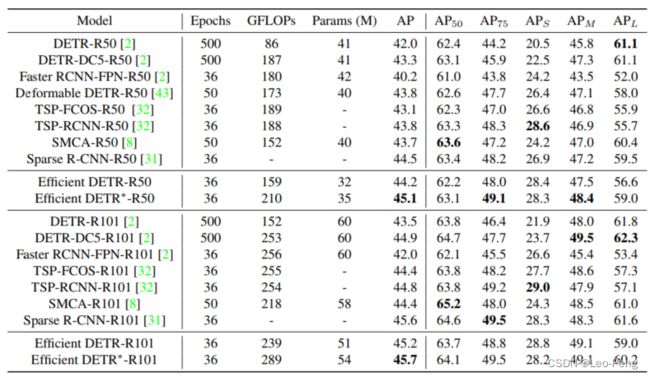
Efficient DETR似乎没有开源，个人觉得Effcient DETR需要依赖一个Dense Part，我觉得耗时应该不会低，不能称作真正意义上的“Efficient”，但是其研究过程还是很能帮助我们去更好地理解DETR这类方法范式的。

2. Anchor DETR

Anchor DETR发表于2022的AAAI，文章的主要思想是通过给每个可学习的Query Embedding赋予明确的物理意义，使其聚焦于特定的区域。

2.1 Anchor Points to Object Query

在原始DETR中，Attention公式如下：$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$$$Q=Q_f+Q_p,K=K_f+K_p,V=V_f,$$对于Decoder中的Self Attention，$K_f，V_f，Q_f\in R^{N_q\times C}$均为解码器的输出，$K_p，Q_p\in R^{N_q\times C}$均为可学习的Positional Embedding$$Q_p=\mathrm{Embedding}\left(N_q,C\right)$$对于Decoder中的Cross Attention，$Q_f\in R^{N_q\times C}$为Self Attention的输出，$K_f\in R^{HW\times C}$和$V_f\in R^{HW\times C}$为编码器的输出特征，$K_p\in R^{HW\times C}$为输出特征的Positional Embedding，$Q_p\in R^{N_q\times C}$仍然由可学西的Positional Embedding生成，生成方式为：$$K_p=g_{sin}\left({\mathrm{Pos}}_k\right)$$$$Q_p=\mathrm{Embedding}\left(N_q,C\right)$$$Q_p\in R^{N_q\times C}$的可解释性比较差，我们只知道它对不同的Query不同，但是有什么不同我们并不知道，因此作者提出将$Q_p\in R^{N_q\times C}$修改为通过Anchor Points生成$$Q_p=g\left({\mathrm{Pos}}_q\right)$$

本文作者是选用了两种类型的锚点：Grid Anchor Points和Learned Anchor Points，如下图所示：

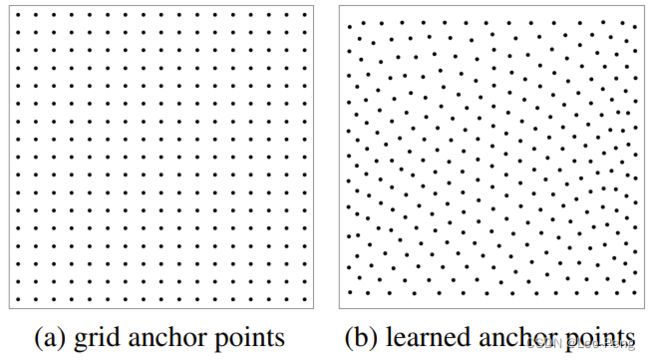
Grid Anchor Points代码如下：

# 均匀网格锚点
nx=ny=round(math.sqrt(self.num_position))
self.num_position=nx*ny
x = (torch.arange(nx) + 0.5) / nx
y = (torch.arange(ny) + 0.5) / ny
xy=torch.meshgrid(x,y)
reference_points=torch.cat([xy[0].reshape(-1)[...,None],xy[1].reshape(-1)[...,None]],-1).cuda()
reference_points = reference_points.unsqueeze(0).repeat(bs, self.num_pattern, 1)

Learned Anchor Points代码如下：

# 可学习锚点
self.position = nn.Embedding(self.num_position, 2) # (300, 2)
nn.init.uniform_(self.position.weight.data, 0, 1)
reference_points = self.position.weight.unsqueeze(0).repeat(bs, self.num_pattern, 1)

基于Anchor Points生成Query Embedding代码如下：

# pos2posemb2d 使用sine、consine函数生成位置编码
# adapt_pos2d 使用MLP微调位置编码
query_pos = adapt_pos2d(pos2posemb2d(reference_points))

作者又考虑到，对于每个锚点可能会存在多个目标，因此作者进一步将$Q_f$的维度设置为$Q_p\in {\mathbb{R}}^{N_p{N}_A\times C}$，即一共有$N_A$个Query，每个Query的维度为$Q_f^i\in R^{N_p\times C}$，即$$Q_f^i=\mathrm{Embedding}\left(N_p,C\right)$$通过$N_p$不会太大，在原始的代码中设置为3。对应代码如下：

# 3, 256
self.pattern = nn.Embedding(self.num_pattern, d_model)
# object queries
# 由于平移不变性，每个object query的pattern的值应该是一样的
# For the property of translation invariance, the patterns are shared for all the object queries
tgt = self.pattern.weight.reshape(1, self.num_pattern, 1, c).repeat(bs, 1, self.num_position, 1).reshape(
            bs, self.num_pattern * self.num_position, c)

通过这样的$Q_p$和$Q_f$构成的Query Embedding具备可解释性，在训练Epoch数少10倍的情况下，依然可以获得比DETR更好的效果。

2.2 Row-Column Decoupled Attention

在本文中，为了降低计算负担，作者还提出了Row-Column Decoupled Attention，即将Key特征解耦为横向特征和纵向特征，如下：$$A_x=\mathrm{softmax}\left(\frac{Q_x{K}_x^T}{\sqrt{d_k}}\right),A_x\in {\mathbb{R}}^{N_q\times W}$$$$Z=\text{ weightedSumW }\left(A_x,V\right),Z\in {\mathbb{R}}^{N_q\times H\times C},$$$$A_y=\mathrm{softmax}\left(\frac{Q_y{K}_y^T}{\sqrt{d_k}}\right),A_y\in {\mathbb{R}}^{N_q\times H}$$$$\text{ Out }=\text{ weightedSumH }\left(A_y,Z\right),\text{ Out }\in {\mathbb{R}}^{N_q\times C}$$$$Q_x=Q_f+Q_{p,x},Q_y=Q_f+Q_{p,y},$$$$Q_{p,x}=g_{1D}\left({\mathrm{Pos}}_{q,x}\right),Q_{p,y}=g_{1D}\left({\mathrm{Pos}}_{q,y}\right)$$$$K_x=K_{f,x}+K_{p,x},K_y=K_{f,y}+K_{p,y}$$$$K_{p,x}=g_{1D}\left({\mathrm{Pos}}_{k,x}\right),K_{p,y}=g_{1D}\left({\mathrm{Pos}}_{k,y}\right),$$$$V=V_f,V\in {\mathbb{R}}^{H\times W\times C}$$其中$\text{ weightedSumW }$和$\text{ weightedSumH }$分别沿着宽度维度和高度维度进行加权，$g_{1D}$表示一维的位置编码。具体代码如下：

# 拆分键的行列特征
k_row = K_row.mean(1)
k_col = k_col.mean(2)

然后依次执行行列注意力：

# 计算行列注意力权重Ax,Ay
scaling = float(head_dim) ** -0.5
q_row = q_row * scaling
q_col = q_col * scaling
attn_output_weights_row = torch.bmm(q_row, k_row.transpose(1, 2))
attn_output_weights_col = torch.bmm(q_col, k_col.transpose(1, 2))
attn_output_weights_col = softmax(attn_output_weights_col, dim=-1)
attn_output_weights_row = softmax(attn_output_weights_row, dim=-1)
# Z=Ax*V
attn_output_row = torch.matmul(attn_output_weights_row,v)
# Out=A_y*Z
attn_output = torch.matmul(attn_output_weights_col,attn_output_row)

最后结果对比三种，在十分之一的训练Epoch数下，Anchor DETR就已经超过原始DETR: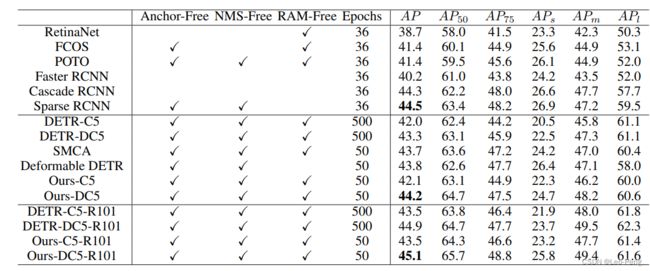
综上所述，Anchor DETR通过Query Embedding中加入Anchor Point的设计，最后Decoder的输出用于回归到每个Anchor Point的偏移量，使得每个Query Embedding只预测Anchor Point附近的目标，简化了优化目标，达到了更好的性能。

3. Conditional DETR

Conditional DETR发表于2021年ICCV，文章的主要贡献是通过Conditional Spatial Query显示地寻找物体的区域范围，从而缩小物体搜索范围，仅仅通过Cross Attention中的微小改动就可以将收敛速度提高6-10倍。

3.1 Attention Maps

和Efficient DETR一样，Conditional DETR的文章中同样也是先对DETR收敛慢的原因进行了一波分析。作者首先可视化了DETR Decoder的Attention Map如下图所示：

其中前三行分别是训练50个Epoch的Conditional DETR的热力图，训练50个Epoch的DETR，训练500个Epoch的DETR，从热力图上看，训练500个Epoch的DETR的结果要明显优于50个Epoch，但是要都劣于Conditional DETR。那么这个Attention Map是如何获得的呢？我们知道MultiHead Attention的公式如下：$$\text{ Attention }(\mathrm{Q},\mathrm{K},\mathrm{V})=\mathrm{softmax}\left(\frac{{\mathrm{QK}}^{\mathrm{T}}}{\sqrt{{\mathrm{d}}_{\mathrm{k}}}}\right)\mathrm{V}$$$$\text{ MultiHead }(\mathrm{Q},\mathrm{K},\mathrm{V})=\mathrm{Concat}\left({\mathrm{head}}_1,\dots ,{\text{ head }}_{\mathrm{h}}\right){\mathrm{W}}^{\mathrm{O}}$$$$\text{ where head }=\text{ Attention }\left({\mathrm{QW}}_{\mathrm{i}}^{\mathrm{Q}},{\mathrm{KW}}_{\mathrm{i}}^{\mathrm{K}},\mathrm{V}{\mathrm{W}}_{\mathrm{i}}^{\mathrm{V}}\right)$$Attention即上述${\mathrm{QK}}^{\mathrm{T}}$部分，在DETR中，每个Head的$\mathrm{Q}$的大小为$850\times 256$，$\mathrm{K}$的大小为$100\times 256$，${\mathrm{QK}}^{\mathrm{T}}$的大小为$856\times 100$，最后经过Softmax和Resize得到$25\times 24\times 1$大小的Attention Maps。正好我在Github找到一位同学分享的DETR的Attention Map的可视化结果链接，l如下图所示：

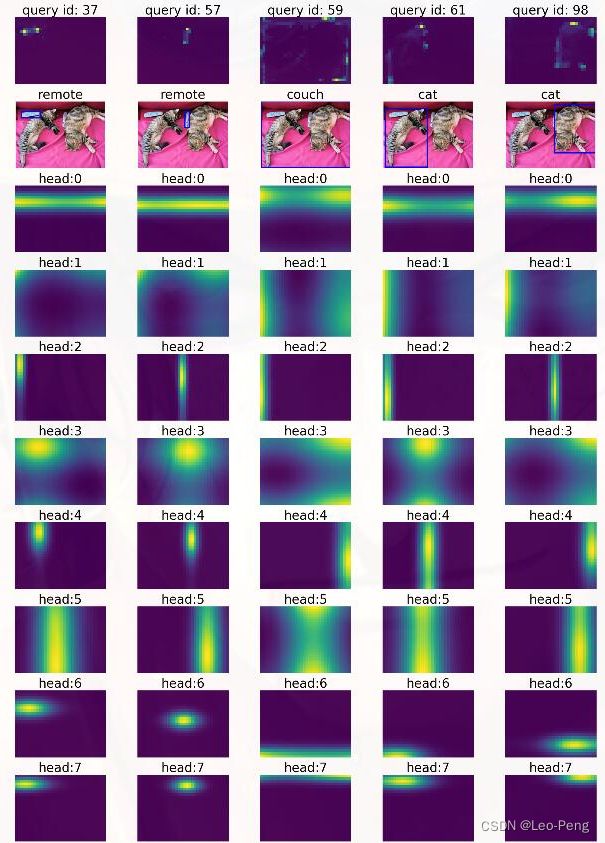
从上述结果中我们可以看到，不同的Head关注不同区域的图像特征，但是同一个Head关注的关注的区域是类似的，比如上述Head2关注的是目标的左边界，Head3关注的目标本身。这一点也很好解释，因为不同Query的Head的从Concat到最后的Detection Branch都是权重共享的，因此不同Query之间的同一位置的Head关注的内容是类似的。在计算机视觉算法——Vision Transformer / Swin Transformer我们也有过类似的分析。

回到问题本身，所以作者认为，DETR收敛慢的原因是Attention Maps没有难以收敛，那么是什么原因导致Attention Maps难以收敛了，文章进一步对Cross Attention的本质进行了分析

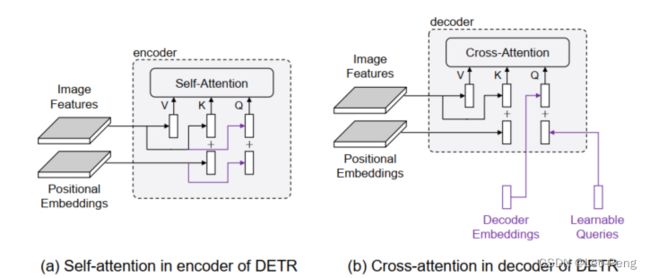
3.2 DETR Decoder Cross-Attention

DETR的结构图下图所示：

其中：

1. 在Decoder中，$\mathrm{K}$是Image Features + Positional Embedding，$\mathrm{Q}$是Decoder Embedding + Object Queriy
2. $\mathrm{Q}$中的Decoder Embedding实际上是上一层Decoder的输出，也就是 $\mathrm{V}$根据Attention Maps取出来的一部分，这个步骤有点类似于Two Stage里面的ROI Pooling，但区别是Cross Atention中取的不是一个区域，而是整个区域经过全局注意力之后的结果；Proposal中的Content信息（内容和图像 颜色、纹理等是相关的）则来源于Decoder Embedding
3. $\mathrm{Q}$中Object Query可以类比是Positional Embedding，仅仅包含了Proposal中的Spatial信息，Spatial代表这个向量它更多包含空间上的信息
4. DETR中将两者Add后继续和Feature计算Attention Maps，继续获取下一层的Decoder Embedding.

有了上述理解后，作者抛出了问题，在DETR中是$\mathrm{Q}$将Content Query $c_q$（Decoder Embedding）和Spatial Query $p_q$（Object Query）相加得到，而$\mathrm{K}$是将Content Key $c_k$（Image Features）和Spatial Key $p_k$（Postional Embedding）相加得到，因此他们进行Cross Attention计算时形式如下：$${\left(c_q+p_q\right)}^{\mathrm{T}}\left(c_k+p_k\right)$$$$=c_q^{\mathrm{T}}{c}_k+c_q^{\mathrm{T}}{p}_k+p_q^{\mathrm{T}}{c}_k+p_q^{\mathrm{T}}{p}_k$$$$=c_q^{\mathrm{T}}{c}_k+c_q^{\mathrm{T}}{p}_k+o_q^{\mathrm{T}}{c}_k+o_q^{\mathrm{T}}{p}_k$$因为Content Query和Spatial Quedy应该是无关的，即Proposal的位置信息和Proposal的内容信息应该是相互独立的，但在DETR的Cross Attention中这两者会相互影响，而前期Content Query的质量不高，因此无法准确地优化Spatial Query，进而导致收敛缓慢。因此作者提出将相加的操作改为Concate，这样两者进行内积变成如下形式：$$c_q^{\mathrm{T}}{c}_k+p_q^{\mathrm{T}}{p}_k$$其中第一项专门负责Content相似度计算，第二项专门负责Spatial相似度计算，互不影响、但是在后续作者的讨论中，作者提到Concat操作并不是他们想要强调的Contribution，并且在DETR中将Add操作修改为Conca操作最终的结果反而下降了，但是重要的是通过上述分析我们知道了DETR收敛困难的核心原因

3.3 Conditional Spatial Query Prediction

根据上面的分析结果，作者提出了Condition Spatial Query的结果如下图所示：

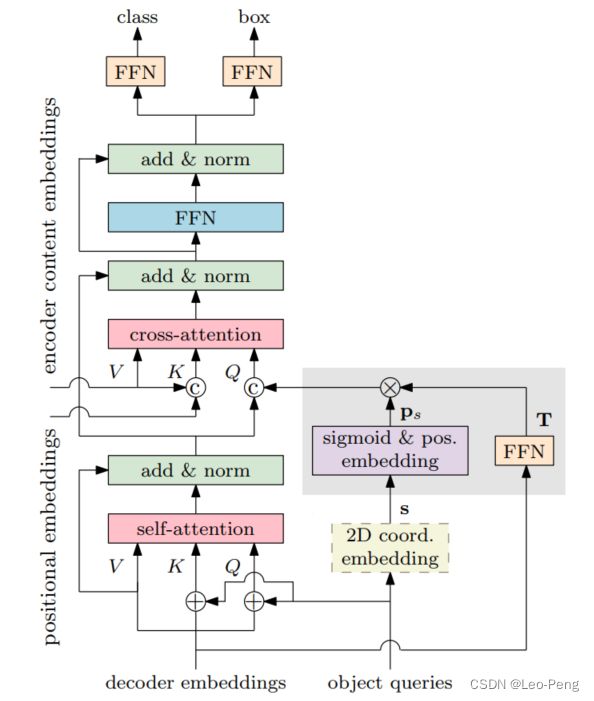
其中：

1. $\mathrm{Q}$和$\mathrm{K}$中的Content Query和Spatial Query的Add操作修改为了Concat操作；
2. $\mathrm{Q}$中的Object Query变成由Reference Points $\mathrm{s}$和Decoder Embedding $\mathrm{f}$两部分构成，即$$(\mathbf{s},\mathbf{f})\to p_q$$其中Reference Point的2D坐标归一化之后映射到和Spatial Key相同的正弦位置编码空间中，得到Reference Point的高维映射：$$p_s=\mathrm{sinusoidal}(\mathrm{sigmoid}(\mathbf{s}))$$而Decoder Embedding通过Feed Forward Network（Linear+ReLU+Linear）映射到高维空间，获得针对Reference Point的偏移量：$$\mathrm{T}=\mathrm{FFN}(\mathbf{f})$$将Reference Point以及对应的偏移量在高维空间相乘就得到最后的Object Query:$$p_q=\mathrm{T}{p}_s={\lambda }_q\odot p_s$$这里的相乘指的其实就是$p_s$和$T$在逐个元素位置上的点乘。在最后Detection Branch部分，Bounding Box的回归结果也变成由Reference Point和偏移量两部分组成：$$\mathbf{b}=\mathrm{sigmoid}\left(\mathrm{FFN}(\mathbf{f})+{\left[\begin{array}{lll}{\mathbf{s}}^{\top }& 0& 0\end{array}\right]}^{\top }\right)$$对于类别的输出还是在Decoder Embedding的基础上通过MLP输出：$$\mathbf{e}=\mathrm{FFN}(\mathbf{f})$$

下面我们通过代码来进一步看下实现的细节，Conditional DETR的代码是基于DETR的工程修改的，下面仅展示修改部分：

# 对应结构图中FFN
class MLP(nn.Module):
    """ Very simple multi-layer perceptron (also called FFN)"""

    def __init__(self, input_dim, hidden_dim, output_dim, num_layers):
        super().__init__()
        self.num_layers = num_layers
        h = [hidden_dim] * (num_layers - 1)
        self.layers = nn.ModuleList(nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim]))

    def forward(self, x):
        for i, layer in enumerate(self.layers):
            x = F.relu(layer(x)) if i < self.num_layers - 1 else layer(x)
        return x

# 将参考点s变成256维度的sincos的编码
def gen_sineembed_for_position(pos_tensor):
    # n_query, bs, _ = pos_tensor.size()
    # sineembed_tensor = torch.zeros(n_query, bs, 256)
    scale = 2 * math.pi
    dim_t = torch.arange(128, dtype=torch.float32, device=pos_tensor.device) # 在0到128维上均匀分布
    dim_t = 10000 ** (2 * (dim_t // 2) / 128)
    x_embed = pos_tensor[:, :, 0] * scale  # 将值的范围放缩到0到2pi
    y_embed = pos_tensor[:, :, 1] * scale
    pos_x = x_embed[:, :, None] / dim_t  # 每一元素除以的dimt的值都不同
    pos_y = y_embed[:, :, None] / dim_t
    pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2)
    pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2)
    pos = torch.cat((pos_y, pos_x), dim=2)
    return pos



class TransformerDecoder(nn.Module):

    def __init__(self, decoder_layer, num_layers, norm=None, return_intermediate=False, d_model=256):
        super().__init__()
        self.layers = _get_clones(decoder_layer, num_layers)
        self.num_layers = num_layers
        self.norm = norm
        self.return_intermediate = return_intermediate
        self.query_scale = MLP(d_model, d_model, d_model, 2)
        self.ref_point_head = MLP(d_model, d_model, 2, 2)
        for layer_id in range(num_layers - 1):
            self.layers[layer_id + 1].ca_qpos_proj = None

    def forward(self, tgt, memory,
                tgt_mask: Optional[Tensor] = None,
                memory_mask: Optional[Tensor] = None,
                tgt_key_padding_mask: Optional[Tensor] = None,
                memory_key_padding_mask: Optional[Tensor] = None,
                pos: Optional[Tensor] = None,  # nn.Embedding(num_queries, hidden_dim)
                query_pos: Optional[Tensor] = None):  # query_pos，从backbone中输出的和feature大小相同的的position embedding
        # 和原始DETR相同，这里的tgt均被初始化为0
        output = tgt

        intermediate = []
        reference_points_before_sigmoid = self.ref_point_head(query_pos)    # [num_queries, batch_size, 2]， 从每一个query embedding中回归出两个坐标点
        reference_points = reference_points_before_sigmoid.sigmoid().transpose(0, 1)
        
		# 开始遍历6层Decoder Layer
        for layer_id, layer in enumerate(self.layers):
        	# 计算中心
            obj_center = reference_points[..., :2].transpose(0, 1)      # [num_queries, batch_size, 2]

			# 计算偏移量
            # For the first decoder layer, we do not apply transformation over p_s
            if layer_id == 0:
                pos_transformation = 1
            else:
                pos_transformation = self.query_scale(output) # 从decoder embedding中计算出偏移量，decoder embeding（tgt）和query embedding维度是相同的

			# 执行Pq = MLP(PE(obj_center))，将中心点转成256维度的嵌入向量
            # get sine embedding for the query vector
            query_sine_embed = gen_sineembed_for_position(obj_center)

			# 中心点乘以偏移量得到最后的Pq
            # apply transformation
            query_sine_embed = query_sine_embed * pos_transformation
            output = layer(output, memory, tgt_mask=tgt_mask,
                           memory_mask=memory_mask,
                           tgt_key_padding_mask=tgt_key_padding_mask,
                           memory_key_padding_mask=memory_key_padding_mask,
                           pos=pos, query_pos=query_pos, query_sine_embed=query_sine_embed,
                           is_first=(layer_id == 0))
            if self.return_intermediate:
                intermediate.append(self.norm(output))

        if self.norm is not None:
            output = self.norm(output)
            if self.return_intermediate:
                intermediate.pop()
                intermediate.append(output)

        if self.return_intermediate:
            return [torch.stack(intermediate).transpose(1, 2), reference_points]

        return output.unsqueeze(0)

其中decoder_layer的forward函数定义如下：

def forward_post(self, tgt, memory, # tgt为初始化为0大小和pos
                 tgt_mask: Optional[Tensor] = None,
                 memory_mask: Optional[Tensor] = None,
                 tgt_key_padding_mask: Optional[Tensor] = None,
                 memory_key_padding_mask: Optional[Tensor] = None,
                 pos: Optional[Tensor] = None,  # nn.Embedding(num_queries, hidden_dim)，在代码中是没有使用的
                 query_pos: Optional[Tensor] = None,  # 从backbone中输出的和feature大小相同的的position embedding
                 query_sine_embed = None, # 通过decoder embedding修正后的query pos
                 is_first = False):
                 
    # ========== Begin of Self-Attention =============
    # Apply projections here 进行特征映射
    # shape: num_queries x batch_size x 256
    q_content = self.sa_qcontent_proj(tgt)      # target is the input of the first decoder layer. zero by default.
    q_pos = self.sa_qpos_proj(query_pos)
    k_content = self.sa_kcontent_proj(tgt)
    k_pos = self.sa_kpos_proj(query_pos)
    v = self.sa_v_proj(tgt)

    num_queries, bs, n_model = q_content.shape # query的个数、batch size、query的channel数
    hw, _, _ = k_content.shape
		
    q = q_content + q_pos  # 在self attention部分是相加
    k = k_content + k_pos

    tgt2 = self.self_attn(q, k, value=v, attn_mask=tgt_mask,
                          key_padding_mask=tgt_key_padding_mask)[0]
    # ========== End of Self-Attention =============

    tgt = tgt + self.dropout1(tgt2)  # dropout
    tgt = self.norm1(tgt)

    # ========== Begin of Cross-Attention =============
    # Apply projections here
    # shape: num_queries x batch_size x 256
    q_content = self.ca_qcontent_proj(tgt)
    k_content = self.ca_kcontent_proj(memory)
    v = self.ca_v_proj(memory)

    num_queries, bs, n_model = q_content.shape # query的个数、batch size、query的channel数
    hw, _, _ = k_content.shape

    k_pos = self.ca_kpos_proj(pos)

    # For the first decoder layer, we concatenate the positional embedding predicted from 
    # the object query (the positional embedding) into the original query (key) in DETR.
    if is_first:
        q_pos = self.ca_qpos_proj(query_pos)
        q = q_content + q_pos
        k = k_content + k_pos
    else:
        q = q_content
        k = k_content

    q = q.view(num_queries, bs, self.nhead, n_model//self.nhead)
    query_sine_embed = self.ca_qpos_sine_proj(query_sine_embed)
    query_sine_embed = query_sine_embed.view(num_queries, bs, self.nhead, n_model//self.nhead)
    q = torch.cat([q, query_sine_embed], dim=3).view(num_queries, bs, n_model * 2) # 将content query和spatial query concate到一起
    k = k.view(hw, bs, self.nhead, n_model//self.nhead)
    k_pos = k_pos.view(hw, bs, self.nhead, n_model//self.nhead)
    k = torch.cat([k, k_pos], dim=3).view(hw, bs, n_model * 2) # 对key进行同样的concate操作

    tgt2 = self.cross_attn(query=q,
                               key=k,
                               value=v, attn_mask=memory_mask,
                               key_padding_mask=memory_key_padding_mask)[0]               
    # ========== End of Cross-Attention =============

    tgt = tgt + self.dropout2(tgt2)
    tgt = self.norm2(tgt)
    tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
    tgt = tgt + self.dropout3(tgt2)
    tgt = self.norm3(tgt)
    return tgt

最后网络输出的部分和原始的DETR也会有区别，如下：

 hs, reference = self.transformer(self.input_proj(src), mask, self.query_embed.weight, pos[-1])
        
reference_before_sigmoid = inverse_sigmoid(reference)
outputs_coords = []
for lvl in range(hs.shape[0]):
    tmp = self.bbox_embed(hs[lvl])
    tmp[..., :2] += reference_before_sigmoid
    outputs_coord = tmp.sigmoid()
    outputs_coords.append(outputs_coord)
outputs_coord = torch.stack(outputs_coords)

outputs_class = self.class_embed(hs)

如上文所述，Box的坐标最终是由Reference Points和通过Decoder Embedding回归的偏移量组合而成，如下图是DETR和Conditional DETR的效果对比，不论是训练速度和评测结果看后者都有明显的优势：

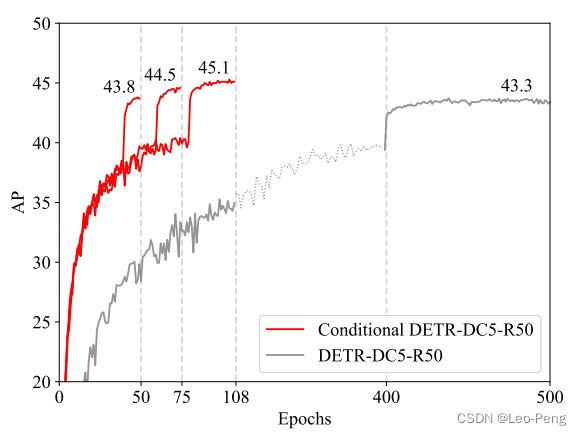
总而言之，Conditional DETR主要进行了两部分改进，首先是解耦了Content Query和Positional Query，减少了训练初期的噪声；其次Positional Query映射成Reference Point（类似于Anchor），并从Content Query中预测偏移量调整Reference Point，这样其实相当于建立了基于偏移量对Query的直接监督。

4. DAB DETR

DAB DETR发表与ICLR 2022，相对Condition DETR，本文的主要区别是使用Dynamic 4D Anchor Box对Query进行建模，即将宽高引入位置先验，使得收敛速度和检测精度进一步提高：

4.1 Analysis on Positional Prior

如同前面两篇文章，本文同样先对收敛慢的原因进行了一波分析，之前的工作已经证明了收敛慢主要是Decoder的问题，作者进一步指出是Decoder中Query的问题，主要是两方面：

1. Query比较难学习
2. Query中没有类似于Positional Embedding的显示的位置先验信息

对于上述第一点，作者使用COCO数据集将Query训练好，然后将Query固定住训练其他模块，结果并没有达到更快的收敛速度，如下图所示：

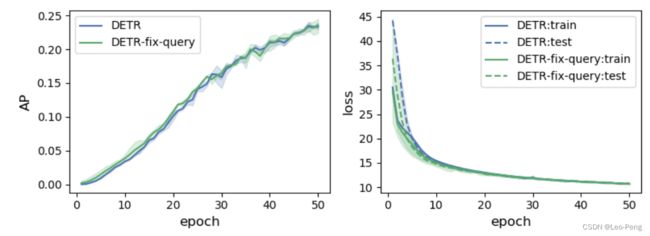
可以看出，即使给Query一个很好的先验也并不会加快收敛速度，因此上述第一点并不是关键原因。对于上述第二点原因，作者可视化了由Positional Query和Position Key构成的Positional Attention Map，DETR、Conditional DETR和DAB DETR三种模型的可视化如下：

从上图中可以看出来，对于DETR，一个Query会关注到多个区域，因此当图片中出现多个物体时，每个Query并不知道自己应该关注哪一个。对于Conditaion DETR，其通过提供二维的位置先验使得每个Query只会关注一个区域，但是每个Query关注的区域都是标准的圆形，忽略了物体尺度大小差异。当然我们也可以观察到，DAB正是因为将宽、高引入位置先验，Query开始关注的物体尺寸大小也不再相同。下面我们直接来看DAB DETR是如何做到这一点的。

4.2 Learning and Update Anchor Box

DAB DETR网络如下图所示：

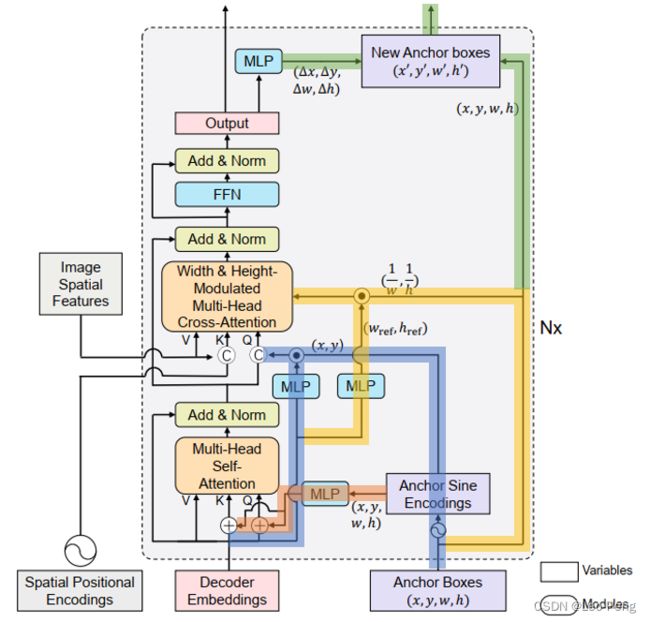
DAB DETR是在Conditional DETR的基础上进行改进的，因此上文在Conditional DETR中介绍的Content Query和Spatial Query在DAB DETR中也是适用的，我们对其中不同的通路打上不同的颜色，其中红色通路是将Anchor Boxes编码Query然后进行Self Attention，编码方式如下：$$P_q=\mathrm{MLP}\left(\mathrm{PE}\left(A_q\right)\right),$$$$\mathrm{PE}\left(A_q\right)=\mathrm{PE}\left(x_q,y_q,w_q,h_q\right)=\mathrm{Cat}\left(\mathrm{PE}\left(x_q\right),\mathrm{PE}\left(y_q\right),\mathrm{PE}\left(w_q\right),\mathrm{PE}\left(h_q\right)\right)$$其中$\mathrm{PE}\left(A_q\right)$操作是指通过一个Positional Encoding函数以及一个MLP将一个浮点数变成Sinusoidal Embedding，对于不同层MLP是参数共享的，在Self Attention中，我们是通过相加操作融合Content Query和Spatial Query：$$Q_q=C_q+P_q,K_q=C_q+P_q,V_q=C_q$$其中蓝色通路和黄色通路是将Anchor Boxes编码Query然后进行Self Attention，其中蓝色通路上先将Anchor Boxes的$x,y$编码进入Query：$$Q_q=\mathrm{Cat}\left(C_q,\mathrm{PE}\left(x_q,y_q\right)\cdot {\mathrm{MLP}}^{(\mathrm{csq})}\left(C_q\right)\right),$$$$K_{x,y}=\mathrm{Cat}\left(F_{x,y},\mathrm{PE}(x,y)\right),V_{x,y}=F_{x,y}$$这一步骤和Conditional DETR中的操作是一致的，会将Decoder Embeding通过一个MLP编码通过点乘修正$\mathrm{PE}\left(x_q,y_q\right)$。如果我们不考虑Anchor Box的长宽的影响，在Cross Attention中，Position Similarity计算如下：$$\mathrm{Attn}\left((x,y),\left(x_{\mathrm{ref}},y_{\mathrm{ref}}\right)\right)=\left(\mathrm{PE}(x)\cdot \mathrm{PE}\left(x_{\mathrm{ref}}\right)+\mathrm{PE}(y)\cdot \mathrm{PE}\left(y_{\mathrm{ref}}\right)\right)/\sqrt{D}$$上图中黄色通路就是将Anchor Box的长宽的影响加入Position Similarity的计算中：$$\mathrm{Modulate}\mathrm{Attn}\left((x,y),\left(x_{\mathrm{ref}},y_{\mathrm{ref}}\right)\right)=\left(\mathrm{PE}(x)\cdot \mathrm{PE}\left(x_{\mathrm{ref}}\right)\frac{w_{q,\mathrm{ref}}}{w_q}+\mathrm{PE}(y)\cdot \mathrm{PE}\left(y_{\mathrm{ref}}\right)\frac{h_{q,\mathrm{ref}}}{h_q}\right)/\sqrt{D}$$其中$w_q$和$h_q$是Anchor Box的长宽，$w_{q,\mathrm{ref}}$和$h_{q,\mathrm{ref}}$是通过Decoder Embedding计算的长宽。加入长宽的编码后，我们可以从不同长宽的物体的特征。

最后，上图中绿色通路是对Anchor进行更新，在DETR和Conditional DETR中，Query都是高维特征因此很难进行逐层Refine，但DAB DETR中使用的是坐标作为Query的表达，因此我们可以通过一个MLP从输出中回归一个修正量$(\Delta x,\Delta y,\Delta w,\Delta h)$对Query的坐标进行修正。其实这里是由疑问的，在红色通路和蓝色通路中我们基于Cross Attention已经使用Decoder Embedding对Anchor信息进行过一次Refine，而这里我们通过绿色通路又进行了一次Refine，这不相当于重复Refine了吗？

下面我们基于源码进一步看下细节，DAB DETR是基于Conditional DETR修改的，我们主要看下修改部分：

def gen_sineembed_for_position(pos_tensor, d_model=256):
    # n_query, bs, _ = pos_tensor.size()
    # sineembed_tensor = torch.zeros(n_query, bs, 256)
    scale = 2 * math.pi
    dim_t = torch.arange(d_model // 2, dtype=torch.float32, device=pos_tensor.device)
    dim_t = 10000 ** (2 * (dim_t // 2) / (d_model // 2))
    x_embed = pos_tensor[:, :, 0] * scale
    y_embed = pos_tensor[:, :, 1] * scale
    pos_x = x_embed[:, :, None] / dim_t
    pos_y = y_embed[:, :, None] / dim_t
    pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2)
    pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2)
    if pos_tensor.size(-1) == 2:
        pos = torch.cat((pos_y, pos_x), dim=2)
    elif pos_tensor.size(-1) == 4:  # 如果pos_tensor的维度是4，则需要将长度和宽度也进行编码
        w_embed = pos_tensor[:, :, 2] * scale
        pos_w = w_embed[:, :, None] / dim_t
        pos_w = torch.stack((pos_w[:, :, 0::2].sin(), pos_w[:, :, 1::2].cos()), dim=3).flatten(2)

        h_embed = pos_tensor[:, :, 3] * scale
        pos_h = h_embed[:, :, None] / dim_t
        pos_h = torch.stack((pos_h[:, :, 0::2].sin(), pos_h[:, :, 1::2].cos()), dim=3).flatten(2)

        pos = torch.cat((pos_y, pos_x, pos_w, pos_h), dim=2)
    else:
        raise ValueError("Unknown pos_tensor shape(-1):{}".format(pos_tensor.size(-1)))
    return pos

class TransformerDecoder(nn.Module):

    def __init__(self, decoder_layer, num_layers, norm=None, return_intermediate=False, 
                    d_model=256, query_dim=2, keep_query_pos=False, query_scale_type='cond_elewise',
                    modulate_hw_attn=False,
                    bbox_embed_diff_each_layer=False,
                    ):
        super().__init__()
        self.layers = _get_clones(decoder_layer, num_layers)
        self.num_layers = num_layers
        self.norm = norm
        self.return_intermediate = return_intermediate
        assert return_intermediate
        self.query_dim = query_dim

        assert query_scale_type in ['cond_elewise', 'cond_scalar', 'fix_elewise']
        self.query_scale_type = query_scale_type
        if query_scale_type == 'cond_elewise':
            self.query_scale = MLP(d_model, d_model, d_model, 2)
        elif query_scale_type == 'cond_scalar':
            self.query_scale = MLP(d_model, d_model, 1, 2)
        elif query_scale_type == 'fix_elewise':
            self.query_scale = nn.Embedding(num_layers, d_model)
        else:
            raise NotImplementedError("Unknown query_scale_type: {}".format(query_scale_type))
        
        self.ref_point_head = MLP(query_dim // 2 * d_model, d_model, d_model, 2)
        
        self.bbox_embed = None
        self.d_model = d_model
        self.modulate_hw_attn = modulate_hw_attn
        self.bbox_embed_diff_each_layer = bbox_embed_diff_each_layer


        if modulate_hw_attn:
            self.ref_anchor_head = MLP(d_model, d_model, 2, 2)

        
        if not keep_query_pos:
            for layer_id in range(num_layers - 1):
                self.layers[layer_id + 1].ca_qpos_proj = None

    def forward(self, tgt, memory,
                tgt_mask: Optional[Tensor] = None,
                memory_mask: Optional[Tensor] = None,
                tgt_key_padding_mask: Optional[Tensor] = None,
                memory_key_padding_mask: Optional[Tensor] = None,
                pos: Optional[Tensor] = None,
                refpoints_unsigmoid: Optional[Tensor] = None, # num_queries, bs, 2
                ):
        output = tgt

        intermediate = []
        reference_points = refpoints_unsigmoid.sigmoid()  # refpoints_unsigmoid是通过nn.Embedding(num_queries, query_dim)进行的初始化，其中query_dim
        ref_points = [reference_points]

        # import ipdb; ipdb.set_trace()        

        for layer_id, layer in enumerate(self.layers):
            obj_center = reference_points[..., :self.query_dim]     # [num_queries, batch_size, 2]
            # get sine embedding for the query vector
            query_sine_embed = gen_sineembed_for_position(obj_center, self.d_model)  
            query_pos = self.ref_point_head(query_sine_embed) 

            # For the first decoder layer, we do not apply transformation over p_s
            if self.query_scale_type != 'fix_elewise':
                if layer_id == 0:
                    pos_transformation = 1
                else:
                    pos_transformation = self.query_scale(output)
            else:
                pos_transformation = self.query_scale.weight[layer_id]

            # apply transformation
            query_sine_embed = query_sine_embed[...,:self.d_model] * pos_transformation

            # modulated HW attentions
            if self.modulate_hw_attn:
                refHW_cond = self.ref_anchor_head(output).sigmoid() # nq, bs, 2， 使用decoder embedding对长宽进行修正
                query_sine_embed[..., self.d_model // 2:] *= (refHW_cond[..., 0] / obj_center[..., 2]).unsqueeze(-1)
                query_sine_embed[..., :self.d_model // 2] *= (refHW_cond[..., 1] / obj_center[..., 3]).unsqueeze(-1)


            output = layer(output, memory, tgt_mask=tgt_mask,
                           memory_mask=memory_mask,
                           tgt_key_padding_mask=tgt_key_padding_mask,
                           memory_key_padding_mask=memory_key_padding_mask,
                           pos=pos, query_pos=query_pos, query_sine_embed=query_sine_embed,
                           is_first=(layer_id == 0))

            # iter update
            if self.bbox_embed is not None:
                if self.bbox_embed_diff_each_layer: # 不同层之前的bbox_embed是否相同
                    tmp = self.bbox_embed[layer_id](output)
                else:
                    tmp = self.bbox_embed(output)
                # import ipdb; ipdb.set_trace()
                tmp[..., :self.query_dim] += inverse_sigmoid(reference_points) # 使用bbox_embed从output中输出bounding box的修正量
                new_reference_points = tmp[..., :self.query_dim].sigmoid() # 修正完后进行归一化
                if layer_id != self.num_layers - 1:  # 最后一层不需要修正
                    ref_points.append(new_reference_points)
                reference_points = new_reference_points.detach()

            if self.return_intermediate:
                intermediate.append(self.norm(output))

        if self.norm is not None:
            output = self.norm(output)
            if self.return_intermediate:
                intermediate.pop()
                intermediate.append(output)

        if self.return_intermediate:
            if self.bbox_embed is not None:
                return [
                    torch.stack(intermediate).transpose(1, 2),
                    torch.stack(ref_points).transpose(1, 2),
                ]
            else:
                return [
                    torch.stack(intermediate).transpose(1, 2), 
                    reference_points.unsqueeze(0).transpose(1, 2)
                ]

        return output.unsqueeze(0)

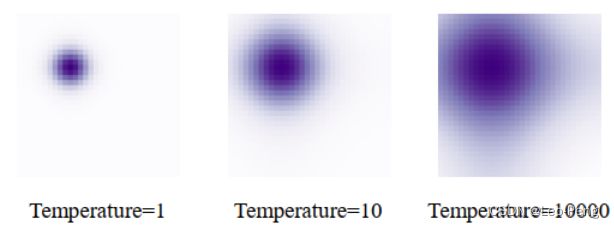
在上述代码中，在gen_sineembed_for_position中有个超参数10000，这个10000对应论文中的参数temperate，对于位置编码，我们使用的是正弦函数：$$\mathrm{PE}(x{)}_{2i}=\sin \left(\frac{x}{T^{2i/D}}\right),\mathrm{PE}(x{)}_{2i+1}=\cos \left(\frac{x}{T^{2i/D}}\right),$$其中，$T$就是超参数temperate，在自然语言处理中$T$被硬编码为10000，$x$为整数表示每个单词在句子中的位置，然而在DETR中，$x$在$0$和$1$之间浮动，代表bounding box的位置，因此对于DETR来说，$T$应该进行调整，在DINO中将$T$设置为了20，$T$越大我们可以理解为不同位置，位置编码区别越小，对应的注意力图会越平坦，如下图所示：

可以看到，代码上的修改并不大，相对于Conditional DETR主要是Cross Attention的过程中加入了长宽对Position Similarity的影响，并在Cross Attention的输出中对Anchor Box的四个参数进行显示的修正。从最后结果看，DAB DETR相对于Conditional DETR在收敛速度和精度上都有提升，如下图所示：