粒子群算法(PSO)以及Matlab实现
粒子群算法(PSO)以及Matlab实现
算法背景
粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation),1995 年由Eberhart 博士和kennedy 博士提出,源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解。
PSO同遗传算法类似,是一种基于迭代的优化算法。系统初始化为一组随机解,通过迭代搜寻最优值。但是它没有遗传算法用的交叉(crossover)以及变异(mutation),而是粒子在解空间追随最优的粒子进行搜索。同遗传算法比较,PSO的优势在于简单容易实现并且没有许多参数需要调整。目前已广泛应用于函数优化,神经网络训练,模糊系统控制以及其他遗传算法的应用领域。
基本原理
假设在一个 D D D维的目标搜索空间中,有 N N N个粒子组成一个群落,其中第 i i i个粒子表示为一个 D D D维的向量
X i = ( x i 1 , x i 2 , … , x i D ) , i = 1 , 2 , … , N X_i=(x_{i1},x_{i2},\dots,x_{iD}),i=1,2,\dots,N Xi=(xi1,xi2,…,xiD),i=1,2,…,N
第 i i i个粒子的速度也是一个 D D D维向量,记为
V i = ( v i 1 , v i 2 , … , v i D ) , i = 1 , 2 , … , N V_i=(v_{i1},v_{i2},\dots,v_{iD}),i=1,2,\dots,N Vi=(vi1,vi2,…,viD),i=1,2,…,N
在第 i i i代的第 i i i个粒子向第 i + 1 i+1 i+1代进化时,根据如下表达式更新
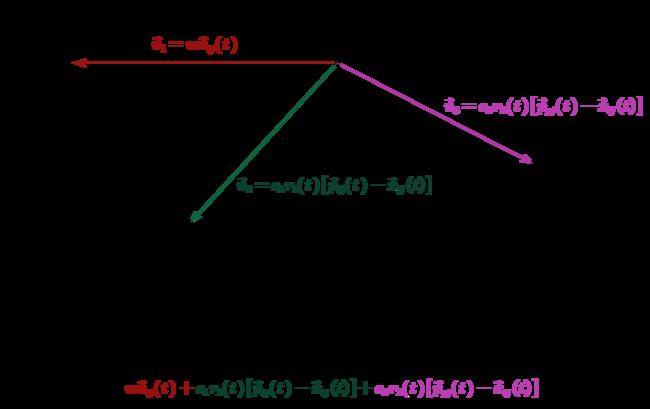
v i j ( t + 1 ) = w v i j ( t ) + c 1 r 1 ( t ) [ p i j ( t ) − x i j ( t ) ] + c 2 r 2 ( t ) [ p g j ( t ) − x i j ( t ) ] x i j ( t + 1 ) = x i j ( t ) + v i j ( t + 1 ) v_{ij}(t+1)=wv_{ij}(t)+c_1r_1(t)[p_{ij}(t)-x_{ij}(t)]+c_2r_2(t)[p_{gj}(t)-x_{ij}(t)]\\x_{ij}(t+1)=x_{ij}(t)+v_{ij}(t+1) vij(t+1)=wvij(t)+c1r1(t)[pij(t)−xij(t)]+c2r2(t)[pgj(t)−xij(t)]xij(t+1)=xij(t)+vij(t+1)
w w w是惯性权重, c 1 c_1 c1是个体学习权重, c 2 c_2 c2是社会学习权重
编程实现
我们给出两个例题
例1:求解 f ( x ) = x sin x cos 2 x − 2 x sin 3 x + 3 x sin 4 x f(x)=x\sin x\cos 2x-2x\sin 3x+3x\sin 4x f(x)=xsinxcos2x−2xsin3x+3xsin4x在 [ 0 , 50 ] [0,50] [0,50]的最小值
%% obj:求解f(x)=xsinxcos2x-2xsin3x+3xsin4x在[0,50]的最小值
%% 初始化
clear
clc
f=@(x)x.*sin(x).*cos(2*x)-2*x.*sin(3*x)+3*x.*sin(4*x);
N=20; %初始化种群个数
d=1; %可行解维数
ger=120; %最大迭代次数
limit=[0,50]; %设置位置参数限制
vlimit=[-10,10];%设置速度最大限制
w=0.8; %惯性权重
c1=0.5; %自我学习因子
c2=0.5; %群体学习因子
figure(1);
ezplot(f,[0,0.01,limit(2)]);
x=limit(1)+(limit(2)-limit(1)).*rand(N,d); %初始种群的位置
v=rand(N,d); %初始种群的速度
xm=x; %每个个体的历史最佳位置
ym=zeros(1,d); %种群的历史最佳位置
fxm=ones(N,1)*inf; %每个个体的历史最佳适应度
fym=inf; %种群历史最佳适应度
hold on
plot(xm,f(xm),'ro');
title('init state');
%% 群体更新
figure(2);
iter=1;
while iter<=ger
fx=f(x); %fx是每个粒子的种群适应度,即每个向量x的函数值fx
for i=1:N
if fx(i)vlimit(2))=vlimit(2);%超过最大速度的粒子限制为最大速度
v(vlimit(2))=limit(2); %超出位置极限的粒子要回到极限位置
x(x 在这里,个体学习因子就是每个粒子历史的最佳适应度对应的位置,社会学习因子就是整个种群的历史最佳适应度对应的位置。
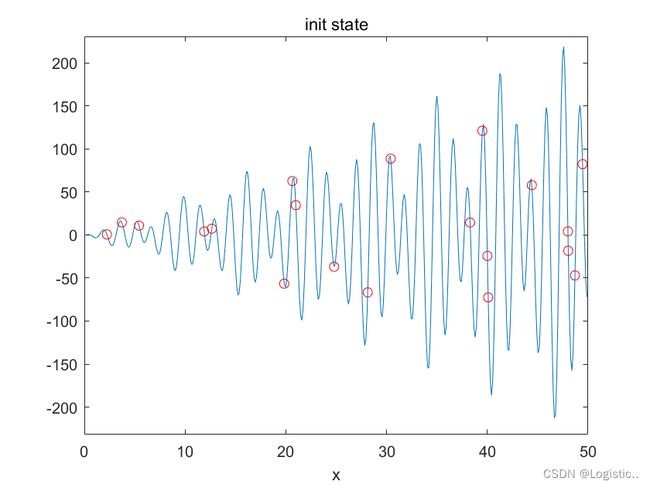
这是初始状态

每当经过10次迭代,记录一次粒子群的位置,可以发现,粒子最终在向最优解收敛

例2:求解 g ( x , y ) = 20 + x 2 + y 2 − 10 cos ( 2 π x ) − 10 cos ( 2 π y ) g(x,y)=20+x^2+y^2-10\cos(2\pi x)-10\cos(2\pi y) g(x,y)=20+x2+y2−10cos(2πx)−10cos(2πy)在 [ − 5.12 , 5.12 ] × [ − 5.12 , 5.12 ] [-5.12,5.12]\times[-5.12,5.12] [−5.12,5.12]×[−5.12,5.12]的最小值
二元函数的情形和一元函数比较相似,上问代码稍作修改即可。
%% obj:求解g(x,y)=20+x^2+y^2-10cos(2*pi*x)-10cos(2*pi*y)在[-5.12,5.12]*[-5.12,5.12]的最小值
clear
clc
%% 初始化
figure(1);
g=@(x,y)20+x.^2+y.^2-10*cos(2*pi.*x)-10*cos(2.*pi*y);
X0=[-5.12:0.05:5.12];
Y0=X0;
[X,Y]=meshgrid(X0,Y0);
Z=g(X,Y);
mesh(X,Y,Z)
colormap(parula(5))
N=50; %初始化种群个数
d=2; %可行解维数
ger=120; %最大迭代次数
limit=[-5.12,5.12]; %设置位置参数限制
vlimit=[-1,1];%设置速度最大限制
w=0.8; %惯性权重
c1=0.5; %自我学习因子
c2=0.5; %群体学习因子
coordinate=limit(1)+(limit(2)-limit(1)).*rand(N,d); %初始种群的位置
v=rand(N,d); %初始种群的速度
local_best=coordinate; %每个个体的历史最佳位置
group_best=zeros(1,d); %种群的历史最佳位置
fit_best_each=ones(N,1)*inf; %每个个体的历史最佳适应度
fit_best_group=inf; %种群历史最佳适应度
hold on
scatter3(local_best(:,1),local_best(:,2),g(local_best(:,1),local_best(:,2)),'r*');%把粒子构成的散点图加到我们的函数图像上
title('init state');
%% 群体更新
iter=1;%iter表示我们的迭代次数,ger是最大迭代次数
while iter<=ger
fit_each=g(coordinate(:,1),coordinate(:,2)); %fit_each是每个粒子的种群适应度,即每个向量(x,y)的函数值g(x,y)
for i=1:N
if fit_each(i)vlimit(2))=vlimit(2);%超过最大速度的粒子限制为最大速度
v(vlimit(2))=limit(2); %超出位置极限的粒子要回到极限位置
coordinate(coordinate 
全局最优解是(0,0),我们可以发现,粒子群正在向(0,0)收敛

题目选自B站up主:青青草原灰太郎