智力题刷题总结

第一组

第一题

农夫需要把狼、羊、菜和自己运到河对岸去，只有农夫能够划船，而且船比较小，除农夫之外每次只能运一种东西，还有一个棘手问题，就是如果没有农夫看着，羊会偷吃菜，狼会吃羊。请按照下列顺序选择合理过河方法（）
A ：农夫单独过河
B ：农夫带狼过河
C ：农夫带羊过河
D ：农夫带菜过河
E ：农夫单独返回
F ：农夫带狼返回
G ：农夫带羊返回
H ：农夫带菜返回

答案：两种方法，方法1：CEBGDEC；方法2：CEDGBEC
解析：
先运菜的话，把羊和狼留下，羊被吃，over。
先运狼的话，把菜和羊留下，菜被吃，over。
只能先运食物链中间的羊。
第一种情况：
①把羊带过河的话，肯定自己返回，要不带它过去干啥子呦。
②然后把狼带过去，狼过去了农夫自己返回羊被吃，所以只能选择把羊拖回去。
③好不容易 把羊拖回来了肯定不能直接再运过去，所以把菜拖过去，狼不吃菜，农夫自己回。
④把羊拖过去。
同理第二种情况：
①把羊带过河的话，肯定自己返回，要不带它过去干啥子呦。
②然后把菜带过去，菜过去了农夫自己返回菜被吃，所以只能选择把羊拖回去。
③好不容易 把羊拖回来了肯定不能直接再运过去，所以把狼拖过去，狼不吃菜，农夫自己回。
④把羊拖过去。

第二题

两个圆环，半径分别是 1 和 2，小圆在大圆内部绕大圆圆周一周，问小圆自身转了几周?

答案：1周
解析：
首先要明白题目的已知条件，除了半径是1:2之外, 可以知道, 小圆圆心速度与小圆与大圆切点的速度, 大小相等, 方向相反(理解这个很关键). 然后小圆绕大圆转一周, 即小圆圆心转以半径之差转一周, 为 2πr, 由于前面的条件, 得小圆圆上的点也是运动了 2πr, 恰好为小圆一周。
同理 如果小圆在大圆外转一周, 小圆圆心运动了 3*2πr, 相当于小圆自身3倍周长. 即小圆转动3周。

第三题

某机器人可以说真话或者假话。某程序设定其周末（周六周日）说真话，周四说谎话，其他日期随机。某测试打算验证该功能。他连续七天，每天问机器人“你在哪里出生的？”，在前六天得到了这样的答案：阿里，淘宝，阿里，淘宝，天猫，淘宝。那么第七天，机器人的回答应该是（）

阿里
淘宝
天猫
阿里或淘宝
阿里或天猫
天猫或淘宝

答案：阿里
解析：
因为答案中没有两个连续相同的，所以第一天只可能是周日或周一
假设第一天的周日，则第七天周六回答应该是周日的阿里，与周四的天猫假话对应，所以这种可能正确
假设第一天是周一，则第七天周日回答应该是周六的淘宝，与周四的淘宝假话冲突，所以这种可能错误
所以第七天回答应该是阿里

第四题

2个人，一人只说真话,一人只说假话,如何去问其中某个人一句话，就分辨出谁是说真话的谁是说假话的。 （）

问任何一人你是说真话的,对吗
指着其中一人问另一人他是说真话的,对吗
只是其中一人问另一人他是说假话的,对吗
做不到

答案：做不到
解析：
本题的选项中没有答案，不过我认为是有解的：
A, B两人，问A：如果我问B你说的是真还是假，他会回答什么；问B：如果我问A你说的是真还是假他会回答什么？
若A真B假：A答假B答真；反之同理

第五题

有三张牌A，B，C，其中一张是King。如果你押中了King，那么就获胜，否则就输。现在你选择了押其中的一张牌1，电脑帮你排除了另外两张牌中的一张2，那么你是否重新选择押3，从而更容易获胜？

无所谓，剩下的两张牌都是50%的羸面
仍然保持我自己的选择1
押3有更大的获胜几率
保持选择1有更大的获胜几率

答案：押3有更大的获胜几率
解析：
情况1，假如我选中的牌1是正确的（概率为1/3），牌3的正确概率为0，
情况2，假如我选中的牌1是错误的(概率为2/3)，牌3正确的概率是1.
综上所述牌3 正确的概率为2/3。
可以参考:三门问题（Monty Hall problem）,亦称为蒙提霍尔问题

第六题

一个5*4的矩阵，有多少个长方形？（正方形也算是长方形）

120
150
100
80

答案：150
解析：
1      2      3      4
5      6      7      8
9      10    11    12
13    14    15    16
17    18    19    20
上面的数字，每一个数字可以看成一个小格子，每一个格子可以说成是一个长方形，算的时候就是求这些边的组合，五行四列的表格有6＊5条边：
竖着取两条边，C(6,2)。横着取两条边C(5,2)
所以结果就是：C(6,2)C(5,2)=1510=150

第二组

第一题

某一密码仅使用 K 、 L 、 M 、 N 、 O 共 5 个字母，密码中的单词从左向右排列，密码单词必须遵循如下规则：
（ 1 ） 密码单词的最小长度是两个字母，可以相同，也可以不同
（ 2 ） K 不可能是单词的第一个字母
（ 3 ） 如果 L 出现，则出现次数不止一次
（ 4 ） M 不能使最后一个也不能是倒数第二个字母
（ 5 ） K 出现，则 N 就一定出现
（ 6 ） O 如果是最后一个字母，则 L 一定出现
问：如果能得到的字母是 K 、 L 、 M ，那么能够形成的两个字母长的密码单词的总数是多少？

1
3
6
9

答案：1
解析：主要是读题
因为只能得到KLM三个字母，而M不能为倒数第一第二位排除，相当于只有KL两个字可以用。
K出现N一起出现排除有K的情况，所以只有一种LL然后LL符合。

第二题

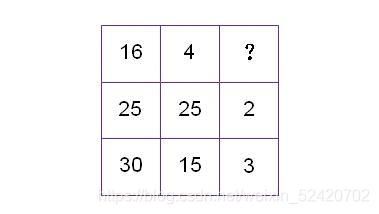
从所给的四个选项中，选择最合适的一个填入“？”处，使图中的数字呈现一定的规律性

5
2
3
6

答案：5
解析：找规律
16/4+1=5；
25/25+1=2；
30/15+1=3

第三题

abcdef六个镇，a与5个有联系，bc与四个有联系，def分别与三个有联系，已知d和f有联系，问e和谁有联系？

A、a，b，c
B、a，c，d
C、a，c，f
D、b，c，f

答案：a，b，c
解析：首先，D是不可能的，a和5个都有联系。然后再看选择部分，三个都有两个共同因素，就是ac，那么e肯定和c有联系，那么剩下的选择中不同的就是b，d，f。df一定和a有联系，而且他们相互也有联系，而他们只有3个联系名额，而再往上一点看，bc与四个有联系，那么就是说，bc必然会占据df的名额，而df没了名额，剩下也只有A答案符合要求了

第四题

在同一侧的房号为1、2、3、4的四间房里，分别住着来自韩国、法国、英国和德国的四位专家。有一位记者前来采访他们
韩国人说：“我的房号大于德国人，且我不会说外语，也无法和邻居交流”；
法国人说：“我会说德语，但我却无法和我的邻居交流”；
英国人说：“我会说韩语，但我只可以和我的一个邻居交流”；
德国人说：“我会说我们这四个国家的语言。”
那么，按照房号从小往大排，房间里住的人的国籍依次是( )。

英国 德国 韩国 法国
法国 英国 德国 韩国
德国 英国 法国 韩国
德国 英国 韩国 法国

答案：德国 英国 法国 韩国
解析：根据韩国人和德国人的描述，韩国在德国后面，且不相邻。只可能有三种情况：
1)__ 德 __ 韩；
2)德 __ __ 韩；
3)德 __ 韩 __ ;
根据法国人的描述，法德不能相邻，排除情况1）
剩下以下两种：
2) 德 __ 法 韩；
3) 德 __ 韩 法；
英国人必然与德国人相邻，因此不能与韩国人相邻，只存在 德 英 法 韩 一种情况；

第五题

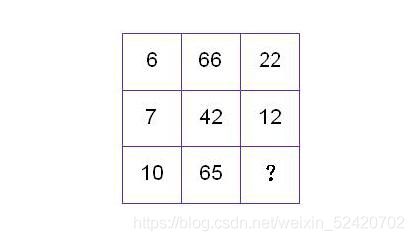
从所给的四个选项中，选择最合适的一个填入“？”处，使图中的数字呈现一定的规律性：

55
48
34
13

答案：13
解析：列B/列A2=列C
622/2 = 66
712/2 = 42
1013/2 = 65

第六题

宿舍内5个同学一起玩对战游戏。每场比赛有一些人作为红方，另一些人作为蓝方。请问至少需要多少场比赛，才能使任意两个人之间有一场红方对蓝方和一场蓝方对红方的比赛？

3
4
5
6

答案：4
解析：这道题可以看成
一次划分中，某方可以有1人，另一方有4人或某方有2人，另一人有3人。
要使任意两个人之间有一场红方对蓝方和蓝方对红方的比赛，假设5个同学为A,B,C,D,E，相当有有向图的5个节点，任意两个节点间有两个方向的边连接。

即总的节点关系有(5个节点中选取两个节点)A(5,2)=5*4=20个关系。

而一次比赛（一次划分）能够生成的关系(一方两人一方三人的划分)c(2,1)×c(3,1)=2×3=6或者（一方四人一方一人的划分)c(4,1)×(c(1,1)=4×1=4,

所以一场比赛(一次划分)最多生成的关系次数为6

所以需要20/6=3.33…即至少需要4场比赛

第三组

第一题

小明、小华和小宝站成一排。小明是其中最大的，他只说真话；第二大的是小华，他只说假话；而最早的小宝有时说真话，有时说假话。小天知道这三个人，但不清楚到底哪个是哪个。他问最左边的这位“你们仨中间的是谁”？回答是“哦，那是小明”。小天随后问中间的这位，“你叫什么”？回答是“我是小宝”。最后小天问最右侧的那位“中间这位是谁”？他得到的回复是“是小华”。那么，这三位的排位顺序从左至右可能是

A 小宝、小明、小华
B 小明、小宝、小华
C 小宝、小华、小明
D 小明、小华、小宝
E 小华、小宝、小明

答案：C
解析：首先假设最左边的是小明，由于他只能说实话，他说中间的是小明，这显然矛盾了，所以假设不成立；
再次假设最左边的是小华，由于他只能说假话，他说中间的是小明，所以小明只能在最右边，中间的应该是小宝。但小明说中间的是小华，这与推论结果冲突；
最后假设最左边的是小宝，
1.假设他说的是真的，中间的是小明，则最右边的是小华。而小明说中间是自己叫小宝，这也矛盾了；
2.假设他说的是假的，则中间应该是小华，最右边应该是小明，正好与题意相符；

第二题

量子力学：物理学：化学，正确选项为（）

A 颜色：黑：白
B 步兵：陆军：空军
C 医院：医生：护士
D 哲学：文学：美学

答案：B
解析：
量子力学属于物理学，而物理学和化学是平行学科
步兵属于陆军，而陆军和空军是平行的

第三题

过 1999 小时 2000 分 2001 秒，时针、分针、秒针正好重合在表盘的“12”上。你 说现在是什么时间 ?

A 7:06:39
B 7:06:29
C 7:16:39
D 8:06:39

答案：A
解析：2001/60=33余21,2001秒化为33分21秒,则经过1999时,33+2000=2033分,21秒
2033/60=33余53分,原时间化为1999+33=2032时,53分,21秒.
由于时钟12小时一个循环,即经12小时后,时分秒针均不变,则2032/12=169余4
则原题转化为：经4小时53分21秒时针,分针,秒针正好重合（即此时为12：00：00整）所以现在时间为07：06：39

第四题

A,B,C,D,E五个人捕鱼后已凌晨，大家便睡觉。早上A第一个醒来，将鱼均分成五份，把多余的一条鱼扔掉，拿走自己的一份，B第二个醒来，也将鱼均分为五份，把多余的一条鱼扔掉，拿走自己的一份。CDE依次醒来，也按同样的方法拿鱼，问他们合伙至少捕了几条鱼。

A 9
B 31
C 3121
D 3906

答案：C
解析：如果多给4条鱼，则5个渔夫每次都恰好可以均分且没有剩余
设多给4条后共有x条鱼。
A取走后剩下：x×4/5；
B取走后剩下：x×4/5×4/5；
C取走后剩下：x×4/5×4/5×4/5；
D取走后剩下：x×4/5×4/5×4/5×4/5：
E取走后剩下：x×4/5×4/5×4/5×4/5×4/5＝x×1024/3125
因为x×1024/3125一定是整数，所以x最少是3125
所以原来的鱼最少有：
3125－4＝3121(条)

第五题

两个大小不同的杯子R和S，R中装着一定量的小米，S中装着一定量的沙子。一名儿童用勺子从S中取出一勺沙子放入R，与小米混合之后，再从R中取出等体积的一勺混合物放入S。假定两勺物品的体积相等，且R和S都没有发生溢出。则以下说法中正确的是多少？

A R中的沙子和S中的小米一样多
B R中的沙子比S中的小米少
C R中的沙子比S中的小米多
D 无法判断

答案：A
解析：假设R中小米体积为X，S中沙的体积为Y，一勺的体积为Z，如果搅拌充分均匀，那么R中的沙的密度为Z/(X+Z)，那么再取出一勺的量则这一勺中沙子的体积为ZZ/(X+Z)，此时R中剩余的沙为Z-ZZ/(X+Z)，而这一勺中小米的体积为Z-Z*Z/(X+Z)，所以两者一样多

第六题

操场上落下了许多好看的花朵，有一朵花有13个花瓣。刘平和王磊用这种花玩一个游戏。他俩轮流去摘花瓣，但规定是每个人只可以摘一片或者相邻的两片，谁摘到最后一片算谁赢。刘平发现，这个游戏好像有规律，于是他坚持后摘花，请问刘平先摘花获得胜利的概率改变了吗？（）

A 获胜几率增加了
B 获胜几率减小了
C 获胜几率不变
D 无法判断

答案：B
解析：根据题干，先手无论拿一或二，你都能在花朵对面位置拿掉一或二，使花瓣变成左五右五的对称结构。之后不管先手怎么拿，后手都拿对面的同样数量。

第四组

第一题

4个人赛跑，要求跑两次算平均排名。已知：A永远不是最后一名，有一个人两次名次相同，C永远比D跑得快，A至少有一个第三名，B至少有一个第一名，D，C两个人都有一个第二名，求两次赛跑的排名情况。

A 第一次为BCAD，第二次为BDAC
B 第一次为BCDA，第二次为CDAB
C 第一次为CDAB，第二次为BCAD
D 以上都不正确

答案：C
解析：cd各有一次第二，而c总d快，那么有一次d为2的时候，c就是1，而d总不为4,因此，当d为2的时候，a为3，b为4，c为1。 而b至少有一次1，那么当c为2的时候b为1，而a为3，d为4.

第二题

一台指针式钟表的时针和分针指向的重合的时间间隔是

A 720/13分钟
B 720/11分钟
C 60分钟
D 以上都不正确

答案：B
解析：时针走一圈，分针走了十二圈，分针多走了十一圈，意味着720分钟内相遇了十一次，所以每次的间隔是720/11分钟。

第三题

甲乙两个一样大小的杯子各自分别装着小于一半容积的水和酒精.现将甲杯子里的一部分水倒入乙杯子;之后将乙杯子的混合液倒入一些到甲杯子,此时甲杯子的液体恢复到最初的状态.假定水和酒精混合之后的体积等于混合之前的体积之和。 那么以下说法正确的是()

A 甲杯子里的酒精体积等于乙杯子里的水的体积
B 甲杯子里的酒精的体积等于乙杯子里的酒精的体积
C 甲杯子里的水的体积等于乙杯子里的酒精的体积
D 甲杯子里的水的体积等于乙杯子里的水的体积
E 甲杯子里的液体高于乙杯子里的液位
F 以上都不对

答案：A
解析：最初，甲杯子只有酒精，乙杯子只有水。
最后，甲杯子恢复到最初的高度，只是混入了一些酒精。
所以从乙杯子拿出多少酒精给甲杯子，乙杯子就有多少甲杯子的水。

第四题

有16瓶水，其中只有一瓶水有毒，小白鼠喝一滴之后一小时会死。请问最少用（） 只小白鼠，在1小时内一定可以找出至少14瓶无毒的水？

A 1
B 3
C 4
D 16

答案：B
解析：将16瓶水两瓶为一组，组号标为A1-A8，三只小白鼠分别标号为b1、b2、b3，A1组水只让b1喝，A2组只让b2喝，A3组只让b3喝，A4组让b1、b2喝，A5组让b1、b3喝，A6组让b2、b3喝，A7组让b1、b2、b3喝，A8组不喝。如果只有b1死了，b2、b3都活着，那么有毒的水在A1组里，剩下的14瓶无毒；如果只有b2死了，b1、b3都活着，则A2组有毒；如果只有b3死了，b1、b2都活着，则A3组有毒；如果b1、b2死，b3活，则A4组有毒；如果b1、b3死，b2活，则A5有毒；如果b2、b3死，b1活，则A6有毒；如果三只全死，A7组有毒；如果三只全活，A8有毒。

第五题

A
B
C
D
E
F
G
H

答案：B
解析：左上角的点1，2，3，4，5，6，7，8，9
右下角的点9，8，7，6，5，4，3，2，1

第六题

假定函数rand_k会随机返回一个[1，k]之间的整数（k＞=2）,并且每个整数值出现的几率相等。已知目前有rand_7的实现，请问通过调用rand_7和四则运算函数，并适当增加逻辑判断和循环等控制逻辑，下列函数可以实现的有______。

A rand_3
B rand_21
C rand_23
D rand_47

答案：A B C D
解析：rand_77 = 7,14,21,28,35,42,49=A
rank_7 = 1,2,3,4,5,6,7=B
A,B任取一个元素求和，这个和出现概率都相同1/71/7.
因此rand_77 + rank_7 = [8,56]的每个元素是等概率的
rand_77 + rank_7 -7= [1,49]的每个元素是等概率的
所以：
int rand_k(){ n=50; while(n>k)n= rand_77 + rank_7 -7;return n;}/ 删去所有大于k的数字 /
但是rand_78这种方式就得不到均匀分布了 ， 因此rank_1,…rank_49均可实现，也只能实现这49中情况。

第五组

第一题

牵牛花对于小喇叭相当于（）对于（）

A 康乃馨，玫瑰
B 纸张，印刷
C 棕榈叶，手掌
D 银河系，太阳系

答案：C
解析：前者和后者只是有某种性质的共同点 且不是一个类别，没有从属关系

第二题

经过破译敌人密码，已经知道了“香蕉苹果大鸭梨”的意思是“星期三秘密进攻”；“苹果甘蔗水蜜桃”的意思是“执行秘密计划”；“广柑香蕉西红柿”的意思是“星期三的胜利属于我们”；那么，“大鸭梨”的意思是（）

A 秘密
B 星期三
C 进攻
D 执行
E 计划

答案：C
解析：“香蕉苹果大鸭梨” ①
“苹果甘蔗水蜜桃” ②
“广柑香蕉西红柿” ③

由①和②可得，苹果代表秘密，
由①和③可得，香蕉代表星期三，
所以大鸭梨代表进攻，答案是C

第三题

使用一辆卡车运输n块单块1TB装满数据的硬盘，以时速80km/h行驶1000km将数据运送到目的地；卡车至少运送（）块硬盘才能使运输速率超1000Gbps。

A 2000
B 3000
C 4000
D 5000
E 6000
F 7000

答案：E
解析：首先注意1000Gbps是1000Gbit每秒，是二进制位，1TB的硬盘是1TB字节，是1024GByte也就是10248Gbit。
80km/h的速度运送1000Km需要12.5小时，也就是12.53600=45000秒
设需要n块硬盘才能到达1000Gbps的速度
则 10248n/45000 >= 1000
计算的n>=5493.164取整也就是至少需要5494块硬盘才能达到这个速度。
选项中满足条件的最下数字是6000，因此选E