二叉树相关算法题总结
二叉树的题,一般都是利用递归来做的,在做题之前,要理解二叉树的遍历,如果对二叉树的遍历,还不是很熟悉,可以参考二叉树的遍历实现
文章目录
-
- 1. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先(简单)
- 2. 剑指 Offer 68 - II. 二叉树的最近公共祖先(中等)
- 3. 剑指 Offer 55 - I. 二叉树的深度(简单)
- 4. 剑指 Offer 55 - II. 平衡二叉树(简单)
- 5. 剑指 Offer 54. 二叉搜索树的第k大节点(简单)
- 6. 剑指 Offer 28. 对称的二叉树(中等)
- 7. 剑指 Offer 26. 树的子结构(中等)
- 8. 剑指 Offer 34. 二叉树中和为某一值的路径
- 9. 剑指 Offer 07. 重建二叉树(中等)
- 10. 重建二叉树(II)(中等)
- 11. 剑指 Offer 32 - II. 从上到下打印二叉树 (简单)
- 12. 剑指 Offer 32 - III. 从上到下打印二叉树 III(中等)
1. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先(简单)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
来源:力扣(LeetCode)
解题思路:
二叉搜索树中,任意一个子树,左孩子都小于父节点,右孩子都大于父节点。所以,可以拿给定的两个结点与父节点比较,如果都小于,则说明最近公共祖先在左子树上,都大于,说明最近公共祖先在右孩子上,一个大于,一个小于,那么最近公共祖先肯定是根结点,整个过程是递归的。
代码
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val > root.val && q.val > root.val) {
return lowestCommonAncestor(root.right, p, q);
}else if(p.val < root.val && q.val < root.val) {
return lowestCommonAncestor(root.left, p ,q);
}else {
return root;
}
}
}
这道题,题目中给出的是二叉搜索树,如果不是二叉搜索树而是普通的树呢?
2. 剑指 Offer 68 - II. 二叉树的最近公共祖先(中等)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:
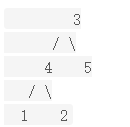
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
来源:力扣(LeetCode)
解题思路:
上面那道题,给的是一棵二叉搜索树,我们可以根据结点值的大小推断出两个结点的最近公共祖先在哪一个子树上,而这道题是一颗二叉树,并不能像上面那道题一样能够推断出最近公共祖先在哪一个子树上,所以,要分别计算,得到两个结果,如果其中一个结果是null,另一个非空的结果就是两个结点的最近公共祖先,如果两个结果都不为null,那么根结点root就是最近公共祖先。
代码
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//root为null,p、q在一个子树上,返回root,遇到p或q,直接返回
if(root == null || root == p || root == q) {
return root;
}
TreeNode l = lowestCommonAncestor(root.left, p, q);
TreeNode r = lowestCommonAncestor(root.right, p, q);
//如果一个为null,就返回另一个,如果两个都不为null,就返回root
if(l == null) {
return r;
}else if(r == null) {
return l;
}else {
return root;
}
}
}
3. 剑指 Offer 55 - I. 二叉树的深度(简单)
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
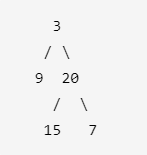
给定二叉树 [3,9,20,null,null,15,7],返回它的最大深度 3 。
提示:
节点总数 <= 10000
解题思路:
二叉树的深度,可以分别计算左子树和右子树的深度,最后拿左子树深度和右子树深度的最大值加1(根节点)。
代码
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right))+ 1;
}
}
还有一种解法,是利用层次遍历,每次遍历一层,res++
class Solution {
public int maxDepth(TreeNode root) {
//层次遍历,每次遍历一层
if(root == null) return 0;
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int res = 0;
while(!queue.isEmpty()) {
int size = queue.size();
for(int i = 0; i < size; i++) {
TreeNode node = queue.poll();
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
res++;
}
return res;
}
}
4. 剑指 Offer 55 - II. 平衡二叉树(简单)
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1:
给定二叉树 [3,9,20,null,null,15,7],返回 true 。
示例 2:
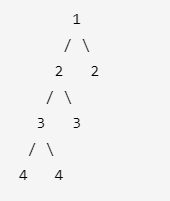
给定二叉树 [1,2,2,3,3,null,null,4,4],返回 false 。
1 <= 树的结点个数 <= 10000
解题思路:
判断一个树是不是平衡二叉树,可以递归的判断左子树、右子树是不是二叉平衡树以及左子树的深度与右子树的深度差小于等于1。
代码
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
return Math.abs(getHeight(root.left)-getHeight(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
public Integer getHeight(TreeNode root) {
if(root == null) return 0;
return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
}
}
另一种写法,在计算深度的时候判断是否平衡,如果平衡就返回深度,不平衡,就返回-1
class Solution {
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
public Integer getHeight(TreeNode root) {
if(root == null) return 0;
int leftHeight = getHeight(root.left);
if(leftHeight == -1) {
return -1;
}
int rightHeight = getHeight(root.right);
if(rightHeight == -1) {
return -1;
}
return Math.abs(leftHeight - rightHeight) > 1 ? -1 : Math.max(leftHeight, rightHeight) + 1;
}
}
5. 剑指 Offer 54. 二叉搜索树的第k大节点(简单)
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
示例2:
解题思路:
二叉搜索树,中序遍历的结果是升序的,所以,将二叉搜索树的中序遍历结果放在一个ArrayList中,返回索引为size-k的元素。
class Solution {
List<Integer> list;
public int kthLargest(TreeNode root, int k) {
list = new ArrayList<>();
dfs(root);
return list.get(list.size() - k);
}
public void dfs(TreeNode root) {
if(root == null) return ;
dfs(root.left);
list.add(root.val);
dfs(root.right);
}
}
利用上面这种解法,空间复杂度是O(n),其实,也可以不用ArrayList,只需将中序遍历逆过来(先遍历右孩子,再遍历父节点,再遍历右孩子)之后,找出第k个元素即可。
class Solution {
int m;
int res;
public int kthLargest(TreeNode root, int k) {
m = k;
dfs(root);
return res;
}
public void dfs(TreeNode root) {
if(root == null) return;
dfs(root.right);
if(--m== 0) {
res = root.val;
return;
}
dfs(root.left);
}
}
剑指 Offer 27. 二叉树的镜像
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
来源:力扣
解题思路:
二叉树的镜像,就是将每一个子树的左孩子和右孩子交换位置,利用递归,获取root的右孩子的镜像,然后将右孩子放到root左孩子上,获取左孩子多的镜像,将左孩子放到root的右孩子上。
代码
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return null;
//将root的左孩子保存下来
TreeNode temp = root.left;
root.left = mirrorTree(root.right);
root.right = mirrorTree(temp);
return root;
}
}
6. 剑指 Offer 28. 对称的二叉树(中等)
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
来源:力扣
解题思路:
判断一个二叉树(根节点root)是否对称,只需递归地判断左子树(根节点root.left)、右子树(root.right)是否对称即可。
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return isSymmetric(root.left,root.right);
}
public boolean isSymmetric(TreeNode root1, TreeNode root2) {
//如果root1 root2都等于空,返回true
if(root1 == null && root2 == null) return true;
//如果只有一个等于空,返回false,肯定不会对称
if(root1 == null || root2 == null) return false;
//如果都不等于空,先判断两个结点值是否相等,再判断root1的左孩子和root2的
//右孩子、root1的右孩子和root2的左孩子是否相等
return root1.val == root2.val && isSymmetric(root1.left, root2.right) && isSymmetric(root1.right, root2.left);
}
}
7. 剑指 Offer 26. 树的子结构(中等)
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
来源:力扣
解题思路:
这道题,要利用双重递归,首先,利用第一个递归遍历A树所有的结点与B比较,判断一个树是否包含另一个树,又是一个递归。
class Solution {
//遍历A树,拿A树中的每个结点和B树对比
public boolean isSubStructure(TreeNode A, TreeNode B) {
if(A == null || B == null) return false;
return helper(A, B) || isSubStructure(A.left,B) || isSubStructure(A.right, B);
}
//判断A这个树是否包含B这个树
public boolean helper(TreeNode A, TreeNode B) {
//如果B==null,返回true
if(B == null) return true;
//A==null,B!=null 返回false
if(A == null) return false;
return A.val == B.val && helper(A.left, B.left) && helper(A.right, B.right);
}
}
- 时间复杂度:O(MN)(M、N分别为A树、B树的结点个数)
- 空间复杂度:O(M)
8. 剑指 Offer 34. 二叉树中和为某一值的路径
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树,以及目标和 sum = 22,
返回:
[ [5,4,11,2], [5,8,4,5] ]
来源:力扣
解题思路:
利用回溯法,深度优先遍历,将遍历过的值放在一个LinkedList中(如果使用ArrayList,可能要扩容,效率没有LinkedList高),每次遍历到叶子结点,如果,不符合条件,就将这个结点,从LinkedList中移出。
代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> temp = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
path(root, sum);
return res;
}
//s代表没有减去root的值之前的值
public void path(TreeNode root, int sum) {
if(root == null) return;
sum = sum - root.val;
temp.add(root.val);
if(root.left == null && root.right == null && sum == 0) {
//注意,要新建一个List
res.add(new LinkedList<>(temp));
}
path(root.left, sum);
path(root.right, sum);
//将结点从LinkedList中移出
temp.removeLast();
}
}
9. 剑指 Offer 07. 重建二叉树(中等)
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
0 <= 节点个数 <= 5000
来源:力扣
解题思路:
前序遍历,按根结点、左孩子、右孩子的顺序,中序遍历,按左孩子、根结点、右孩子的顺序,前序遍历的第一个结点的就是根结点,找出根结点在中序遍历中的位置,那么,这个结点前面的元素就是左子树,后面的元素就是右子树,之后,再根据左右子树的前序遍历、中序遍历重复上述过程(递归)
代码
class Solution {
Map<Integer,Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
//将中序遍历的结果放到map中,便于查找
for(int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return build(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
}
/*ps、pe是先序遍历中,一个子树的起始位置和结束位置
is、ie是中序遍历中,一个子树的起始位置和结束位置
*/
public TreeNode build(int[] preorder, int [] inorder, int ps, int pe, int is, int ie) {
if(ps > pe) return null;
TreeNode newNode = new TreeNode(preorder[ps]);
if(ps == pe) return newNode;
int i = map.get(preorder[ps]);
//根据i的位置,算出newNode的坐子树中结点个数
int count = i - is;
//根据i、count写出newNode的左子树在前序、中序遍历中的元素位置
newNode.left = build(preorder, inorder,ps + 1, ps + count, is, i - 1);
//写出newNode的右子树在前序、中序遍历中的位置
newNode.right = build(preorder,inorder,ps + count + 1, pe, i + 1, ie);
return newNode;
}
}
学会了怎么根据前序遍历和中序遍历能够重建二叉树,那么,根据后序遍历和中序遍历重建二叉树,也非常的简单。
10. 重建二叉树(II)(中等)
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
解题思路:
后序遍历,是按照左孩子、右孩子、根节点的顺序遍历的,后序遍历中,第一个元素就是根结点。
代码:
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return build(postorder, inorder, 0, postorder.length - 1, 0, inorder.length - 1);
}
public TreeNode build(int[] postorder, int[] inorder, int ps, int pe, int is, int ie) {
if(ps > pe) return null;
TreeNode newNode = new TreeNode(postorder[pe]);
if(ps == pe) return newNode;
int i = map.get(postorder[pe]);
int count = i - is;
newNode.left = build(postorder, inorder, ps, ps + count - 1, is, i - 1);
newNode.right = build(postorder, inorder, ps + count, pe - 1, i + 1, ie);
return newNode;
}
}
11. 剑指 Offer 32 - II. 从上到下打印二叉树 (简单)
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7]

返回其层次遍历结果:
[ [3], [9,20], [15,7] ]
来源:力扣
解题思路:
利用层次遍历,先记录队列的大小,然后根据这个值,进行循环的出队入队操作。
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) return new ArrayList<List<Integer>>();
List<List<Integer>> res = new ArrayList<List<Integer>>();
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
//提前记录size值
int size = queue.size();
List<Integer> list = new ArrayList<>();
//根据size值进行出队入队操作,不管当前队列的大小
for(int i = 0; i < size; i++) {
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
res.add(list);
}
return res;
}
}
12. 剑指 Offer 32 - III. 从上到下打印二叉树 III(中等)
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:
给定二叉树: [3,9,20,null,null,15,7],

返回其层次遍历结果:
[ [3],[20,9], [15,7] ]
来源:力扣
解题思路:
这道题和上面的题思路差不多,唯一不同的是需要定义一个boolean类型变量flag,当flag为true时,使用addLast方法将结点值装入LinkedList,当flag为false时,使用addFirst方法,将结点值装入LinkedList。
代码
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root == null) return res;
Deque<TreeNode> deque = new LinkedList<>();
boolean flag = true;
deque.offer(root);
while(!deque.isEmpty()) {
LinkedList<Integer> temp = new LinkedList<>();
int size = deque.size();
while(size > 0) {
TreeNode cur = deque.poll();
if(flag) {
temp.addLast(cur.val);
}else {
temp.addFirst(cur.val);
}
if(cur.left != null) deque.offer(cur.left);
if(cur.right != null) deque.offer(cur.right);
size--;
}
flag = !flag;
res.add(temp);
}
return res;
}
}