C++实现前缀和与差分
前缀和
前缀和的含义是给定一个原数组a[],然后我创建一个数组b[],使得数组b中[i] = a[0] + a[1] + ... + a[i],也就是说b数组的第i项是a数组前i项的和。
前缀和存在的意义是它可以把原本时间复杂度为O(N)的题目用O(1)解出来,比如说下面这道题目:
题目:前缀和
输入一个长度为 n 的整数序列。
接下来再输入 mm 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 mm 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式
共 mm 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n, 1≤n,m≤100000, −1000≤数列中元素的值≤1000
输入样例:
5 3 2 1 3 6 4 1 2 1 3 2 4
输出样例:
3 6 10
题目的意思是给你一个数组,让你求几个区间内数组元素的和,这道题一开始都会想到循环遍历指定的区间,然后依次输出结果,但是如果你得到了它的前缀和数组,你可以直接根据它给你的区间求出结果,比如说在[l, r]这个区间,可以得到结果是 b[r] - b[l - 1]。
模板:
S[i] = a[1] + a[2] + ... a[i] a[l] + ... + a[r] = S[r] - S[l - 1]
代码:
#include
using namespace std;
const int N = 1e6 + 10;
int main(){
int n, m; // n表示数组长度,m表示需要求出几组结果
int a[N], s[N];
scanf("%d%d", &n, &m); //
for(int i = 1; i <= n; i++) scanf("%d", &a[i]); // 保存输入的数组
for(int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i]; // 求出a数组的前缀和数组
while(m--){
int l, r; // 保存指定的区间
scanf("%d%d", &l, &r);
cout << s[r] - s[l - 1] << endl; // 根据公式直接得出结果
}
return 0;
} 根据上面这道题可以扩展到二维数组,也是同样的道理,如下面这道题:
题目:子矩阵的和
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 mm 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q 行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000, 1≤q≤200000, 1≤x1≤x2≤n, 1≤y1≤y2≤m, −1000≤矩阵内元素的值≤1000−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3 1 7 2 4 3 6 2 8 2 1 2 3 1 1 2 2 2 1 3 4 1 3 3 4
输出样例:
17 27 21
这道题也同样是要求出某一个范围内的数的和,只不过是扩展到了二维,如下图:
数组b中的第i行第j列的元素为a数组中第i行第j列它左上角所有数的和,根据这一性质可以得到上面这个公式,根据这个公式就可以得出答案。
模板:
S[i, j] = 第i行j列格子左上部分所有元素的和 以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为: S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
代码:
#include
using namespace std;
const int N = 1010;
int main(){
int n, m, q;
int a[N][N], s[N][N];
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%d", &a[i][j]); // 从控制台读取数据
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; // 得到a数组的前缀和数组
while(q--){
int x1, x2, y1, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;
}
return 0;
} 差分
差分跟前缀和是反过来的,它是给定一个数组a,我自己创建一个数组b,让a数组是b数组的前缀和,根据这一定理也可以
题目:差分
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 l,r 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 mm 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000, 1≤l≤r≤n, −1000≤c≤1000, −1000≤整数序列中元素的值≤1000
输入样例:
6 3 1 2 2 1 2 1 1 3 1 3 5 1 1 6 1
输出样例:
3 4 5 3 4 2
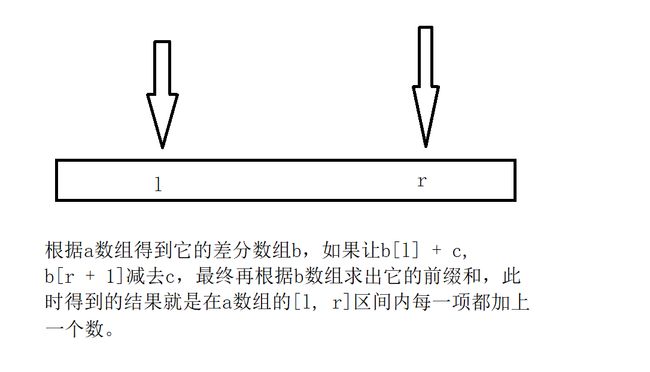
这道题就是说让你在给定数组的某一个区间内所有数都加上一个数,那么为什么要用差分呢?见下图
根据这一性质就可以开始解决本道题了
模板:
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
代码:
#include
using namespace std;
void insert(int b[], int l, int r, int c){
b[l] += c;
b[r + 1] -= c;
}
int main(){
const int N = 100010;
int a[N], b[N];
int n, m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]); // 从控制台读取数据
for(int i = 1; i <= n; i++) insert(b, i, i, a[i]); // 根据a数组求出它的差分数组b
while(m--){
int l, r, c; // 从控制台读取区间以及加的那个数
scanf("%d%d%d", &l, &r, &c);
insert(b, l, r, c);
}
for(int i = 1; i <= n; i++){
b[i] += b[i - 1]; // 再根据b数组求出差分数组,直接输出
cout << b[i] << " ";
}
return 0;
} 同样也是把它扩展到二维数组中:
题目:差分矩阵
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 cc。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 mm 个整数,表示整数矩阵。
接下来 q 行,每行包含 55 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000, 1≤q≤100000, 1≤x1≤x2≤n, 1≤y1≤y2≤m, −1000≤c≤1000, −1000≤矩阵内元素的值≤1000
输入样例:
3 4 3 1 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 1 1 3 2 3 2 3 1 3 4 1
输出样例:
2 3 4 1 4 3 4 1 2 2 2 2
跟上面那道题同样的道理,也是创建出它的差分矩阵,然后按照下面的模板进行操作,最后也同样的求出它的前缀和就是结果了
模板:
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c: S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
代码:
#include
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
// 这一步操作后求出b数组的前缀和就是答案
void insert(int x1, int y1, int x2, int y2, int c){
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main(){
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%d", &a[i][j]); // 从控制台读取数据
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m ; j++)
insert(i, j, i, j, a[i][j]); // 得到原数组的差分矩阵
while(q--){
int x1, x2, y1, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c); // 按照题目要求在指定区域加上c
}
for(int i = 1; i <= n ; i++)
for(int j = 1; j <= m; j++)
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; // 求前缀和
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
printf("%d ", b[i][j]);
}
cout << endl;
}
return 0;
} 以上就是本次介绍的全部内容了。