数学建模之Python-图论算法模型
前言
下面来介绍一下图论模型中的各个算法的基本原理和在Python中的建模仿真;
np.zero用法老忘 再记记
zip和dict用法
https://blog.csdn.net/qq_36825778/article/details/103093807?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162925767216780357257948%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=162925767216780357257948&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduend~default-2-103093807.first_rank_v2_pc_rank_v29&utm_term=dict%E5%92%8Czip&spm=1018.2226.3001.4187
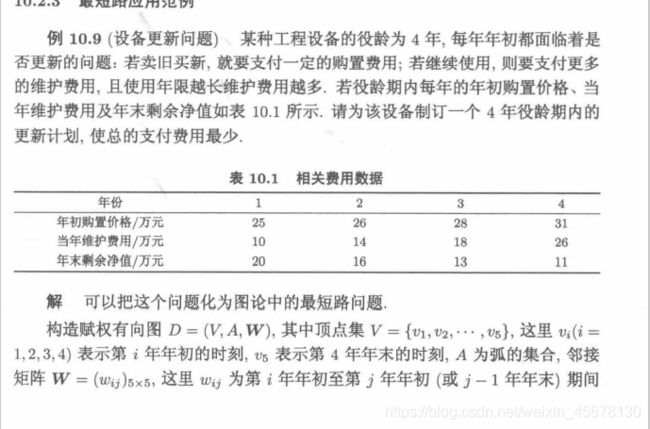
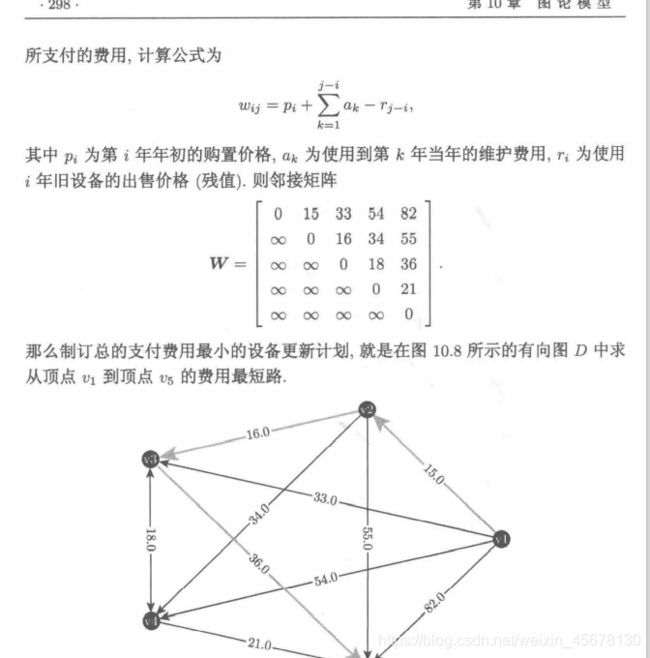
模型一:最短路算法的应用:
代码(DJ)
import numpy as np
import networkx as nx
import pylab as plt
p=[25,26,28,31]
a=[10,14,18,26]
r=[20,16,13,11]
b=np.zeros((5,5))
for i in range(5):
for j in range(i+1,5):
b[i,j]=p[i]+np.sum(a[0:j-i])-r[j-i-1]
print(b)
G=nx.DiGraph(b)
p=nx.dijkstra_path(G,source=0,target=4,weight='weight')
print("最短路径为:",np.array(p)+1)
d=nx.dijkstra_path_length(G,0,4,weight='weight')
print("所需费用的最小值:",d)
s=dict(zip(range(5),range(1,6)))
print(s)
plt.rc('font',size=16)
pos=nx.shell_layout(G) #设置布局
w=nx.get_edge_attributes(G,'weight')
nx.draw(G,pos,font_weight='bold',labels=s,node_color='r')
nx.draw_networkx_edge_labels(G,pos,edge_labels=w)
path_edges=list(zip(p,p[1:]))
nx.draw_networkx_edges(G,pos,edgelist=path_edges,
edge_color='r',width=3)
plt.savefig("figure10_9.png",pdi=500); plt.show()
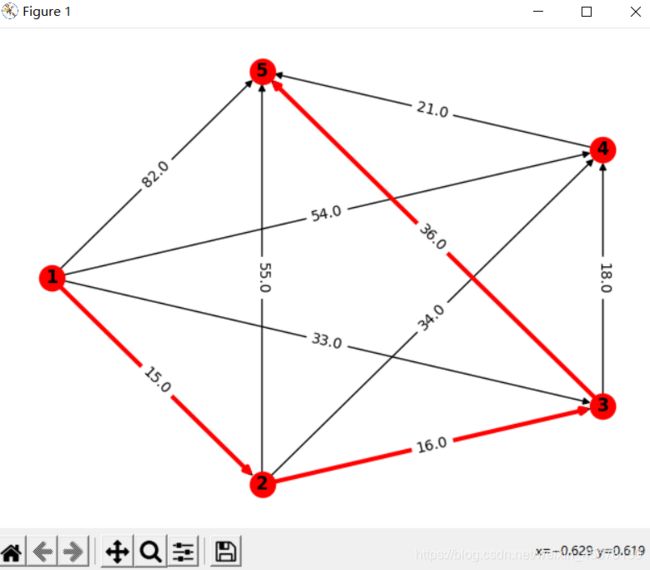
运行截图
模型二:重心问题
代码:
#程序文件Pex10_10.py
import numpy as np
import networkx as nx
List=[(1,2,20),(1,5,15),(2,3,20),(2,4,40),
(2,5,25),(3,4,30),(3,5,10),(5,6,15)]
G=nx.Graph()
G.add_nodes_from(range(1,7))
G.add_weighted_edges_from(List)
print(G)
c=dict(nx.shortest_path_length(G,weight='weight'))
d=np.zeros((6,6))
for i in range(1,7):
for j in range(1,7): d[i-1,j-1]=c[i][j]
print(d)
q=np.array([80,90,30,20,60,10])
m=d@q #计算运力,这里使用矩阵乘法
mm=m.min() #求运力的最小值
ind=np.where(m==mm)[0]+1 #python下标从0开始,np.where返回值为元组
print("运力m=",m,'\n最小运力mm=',mm,"\n选矿厂的设置位置为:",ind)
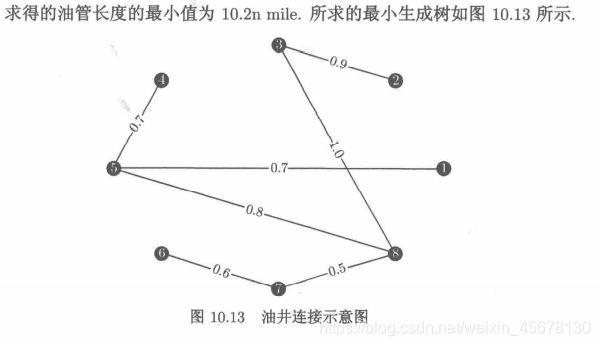
模型三:最小生成树问题
代码:
#程序文件Pex10_14.py
import numpy as np
import networkx as nx
import pandas as pd
import pylab as plt
a=pd.read_excel("Pdata10_14.xlsx",header=None)
print(a)
b=a.values;
print(b)
b[np.isnan(b)]=0
print(b)
c=np.zeros((8,8)) #邻接矩阵初始化
c[0:7,1:8]=b #构造图的邻接矩阵
G=nx.Graph(c)
T=nx.minimum_spanning_tree(G) #返回可迭代对象
d=nx.to_numpy_matrix(T) #返回最小生成树的邻接矩阵
print("邻接矩阵c=\n",d)
W=d.sum()/2+5 #求油管长度
print("油管长度W=",W)
s=dict(zip(range(8),range(1,9))) #构造用于顶点标注的标号字典
plt.rc('font',size=16); pos=nx.shell_layout(G)
nx.draw(T,pos,node_size=280,labels=s,node_color='r')
w=nx.get_edge_attributes(T,'weight')
nx.draw_networkx_edge_labels(T,pos,edge_labels=w)
plt.savefig('figure10_14.png'); plt.show()
ps:
经过values方法变成二维数组 isnan将nan的全变为0
模型四:匹配问题
import numpy as np
import networkx as nx
from networkx.algorithms.matching import max_weight_matching
a=np.array([[3,5,5,4,1],[2,2,0,2,2],[2,4,4,1,0],
[0,2,2,1,0],[1,2,1,3,3]])
b=np.zeros((10,10)); b[0:5,5:]=a; G=nx.Graph(b)
s0=max_weight_matching(G) #返回值为(人员,工作)的集合
s=[sorted(w) for w in s0]
L1=[x[0] for x in s]; L1=np.array(L1)+1 #人员编号
L2=[x[1] for x in s]; L2=np.array(L2)-4 #工作编号
c=a[L1-1,L2-1] #提取对应的效益
d=c.sum() #计算总的效益
print("工作分配对应关系为:\n人员编号:",L1)
print("工作编号:", L2); print("总的效益为:",d)