《深入浅出基础篇》P1872 美国混血， 已知前序中序求后序

这道题就是：给你前序遍历，中序遍历的结果让你输出后续遍历。

所以，这篇题解主要有以下几个内容：

1，已知二叉树求前序遍历

2，已知二叉树求中序遍历

3，已知二叉树求后序遍历

4，由前序遍历+中序遍历如何求出整个二叉树

5，代码实现

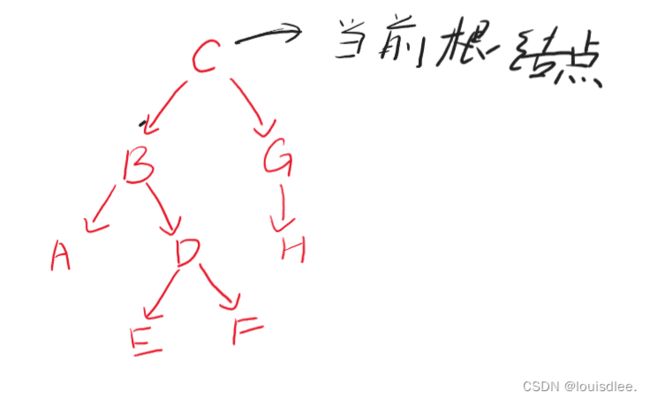
先给一个二叉树：

前序遍历：一句话：“根左右”，从最上面开始，先找到根节点，然后从根节点开始遍历左子树，再遍历右子树。

 找到根节点：

现在序列为：C，然后遍历左子树，而遍历左子树的方法也是一模一样，找左子树的根节点，遍历左子树的根节点的左子树，再遍历其右子树。

 

 这棵数的根节点是B。

现在序列里面是 CB

然后先遍历B的左子树，A

这颗左子树的根结点就是A，所以将A放进来，当前序列就是CBA

然后A没有子树，所以回去遍历B的右子树，右子树的根节点是D，将D放进来，所以序列就是CBAD。

以此类推，最终结果就是CBADEFGH

这就是这颗二叉树的先序遍历结果。

中序遍历：一句话：左根右，先从最底部且最左边找第一个根节点，先遍历该根节点的左子树，再遍历根节点，再遍历其右子树，然后继续找根节点

 第一个根节点是A，但是它的左右子树不存在，所以直接将A加入序列，继续次左边的就是A的根节点B

由于B 是有左右子树的，所以先遍历B的左子树，就是A，因为A已经加入过了，这次不加

再遍历根节点，也就是B本身，将B加入序列，

然后遍历B的右子树，DEF

遍历B的右子树又是一样的步骤，从这棵树最左边根节点E，将其加入序列

然后找到E的根节点D，遍历D的左子树，E（已经加入过了），

再将D放入序列，最后将F放入序列，

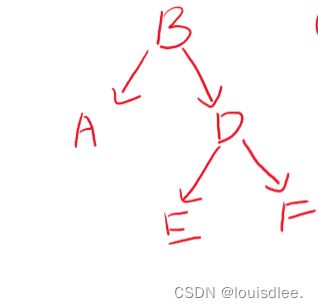
至此以B为根节点的树的中序遍历为：ABEDF

然后继续从B往上找，找到C，将C加入序列：ABEDFC

以C为根节点，左子树和根节点都已经遍历过了，所以现在遍历C的右子树，

还是一样的配方，得到HG

所以这棵树的中序遍历就是：ABEDFCHG

后序遍历：一句话：“左右根”

和中序遍历差不多，只不过把根节点放在最后了。

从最左边找节点：A，将A放入序列

然后先找B的左子树：A（已经存放过了）

找B的右子树：（同样的配方可以得到：）EFD，放入序列

最后再放入B，所以得到：B树的后序遍历：AEFDB

然后从B向上找，根节点为C，由于C的左子树（也就是B树）已经找完了，所以找右子树

C的右子树：HG

所以C树的后序遍历就是：AEFDBHGC

其实我们可以发现，他们的遍历都是可以用DFS来写的，照着思路 写就可以了。

现在已知前序遍历，中序遍历，如何求后序遍历？

前序遍历：CBADEFGH

中序遍历：ABEDFCHG

我们可以通过前序遍历的第一个字母来找到当前树的根节点：C

然后查找C再中序遍历的位置：下标是5（下标从0开始）

 那么我们可以得到：

中序遍历中C的左子树就是：ABEDF

中序遍历中C的右子树是：HG

前序遍历中C的左子树：BADEF

前序遍历中C的右子树：GH

我们由这四个结果可以得到两颗树的前序和中序遍历，

左子树：前序：BADEF 中序：ABEDF

右子树：前序：GH   中序：HG

然后按照这个步骤先递归处理左子树，dfs（左子树），再递归处理右子树dfs（右子树）

最终我们会按照上面后序遍历的过程逐渐回溯，每次回溯都会输出当前根节点。

因为是先处理左子树，最终dfs到达的位置一定是整棵树的最左边A，输出A

然后回溯到B，处理了B的右子树DEF，由于右子树有分支，所以最终的输出是E->F->D

然后右子树处理完了，回到B，输出根节点B

以此类推

得到后序遍历AEFDBHGC

由于我们需要用到前序遍历和中序遍历结果，所以我们干脆直接把前序遍历和中序遍历的结果作为参数传入dfs中，然后上述的，查找，将遍历结果划分两部分的操作就是用find，和substr实现的

上代码：

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include