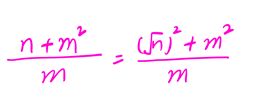谈谈我对普通莫队和带修莫队的拙见

对于莫队，本质上就是分块+暴力。

下面讲一下我当时的心路历程（2333），并不能当教程，可以当故事看看菜鸡初学完莫队之后是怎么想的。

普通莫队：

最普通的情况，给一个长度为n的数组，有q个询问，每次询问[l,r]区间内的最值

假如询问刚好是[3,5]区间和[3,6] 区间，并且我已经通过朴素方法求得[3,5]区间的答案，我并不需要再朴素求一遍后者的答案，我可以利用先前已经得到的信息，从[3,5]到[3,6]，只需要考虑下标为6这个数是否大于[3,5]区间的最大值，是的话那么最大值就是下标为6的这个数。

这也就是最最基础的思想，假如我知道[l,r]区间的答案，我能够在常数的时间推出[l+1,r]，[l-1,r],[l,r+1],[l,r-1]这四个区间的答案，那么我们就可以将所有询问的区间保存下来，寻找一种遍历区间的路径使得能够在最少操作步数内通过左右区间递推的情况访问完所有区间。

我最开始学习的时候，第一个想法就是对询问区间排序，左端点为第一关键字，右端点为第二关键字，如此升序排列。

但是这种排序方法十分不稳定，因为对于区间长度变化很大的询问，这种方法就会被卡掉，比如 [1,2],[2,200],[3,4],[4,201]，如此右指针需要不断跨越大区间。

其实对于寻找最短路径遍历完所有区间，是存在数据结构解决该问题的，就是曼哈顿树。两个区间之间的距离刚好是abs(l1-l2)+abs(r1-r2) 是横纵坐标之差，就是曼哈顿距离。但是假如这样做就违背了用莫队的初衷，我们需要代码量更少的做法。（其实我在这之前并不知道曼哈顿树哈哈哈哈）

既然按左端点排序不好，那么我们可以扩大范围，就是在一个范围内的左端点都视为相同，对于此方位的区间就按照右端点排序。

对于[1,2],[2,200][3,4]  ，假如我们定义的范围足够大，比如说范围从1开始长度为4，那么这三个数组左端点都在同一个区间内，此时按照右端点排序，那就是[1,2][3,4][2,200] 

这样是不是稍微缓解了一下尴尬的局面2333.

那么问题就来了，我们该如何分块，也就是说一个范围的长度。那么我们来简单计算一下，还是刚开始的那个问题，询问l，r区间内的最大值

设分块长度为m，总区间长度为n，那么分块的数量就为 n/m ，长度不足m的独立出来暴力求解，那么分块最多剩下两边各为m的长度，加起来是2m，块和块之间可以常数时间求解，即O（1）求解，那么总的时间复杂度应该是 O(n/m+m) （省略数字)

通分一下：

根据不等式则可知道当m=sqrt(n)的时候分块策略最好

分块的大小需要计算，但是对于莫队来说最好的长度是 O^(2/3)   ,假如时间卡的不紧的话sqrt（n）就可以了

 

下面就来讲讲优化，对于莫队的优化可以体现在不同的地方，下面我讲一个：

奇偶排序优化：

按照上面的说法，假如当左端点处于同一块的时候，我们总是按右端点升序，但这种方法并不是很好的。

当左端点处于奇数块的时候，我们按照右端点升序，当其处于偶数块的时候，我们按照右端点降序。

其实也很好理解，前一块按照右端点升序排列，最后右指针一定处于最右边，那么下一块的排序就按右端点降序，这样能减少右指针移动的次数 

 

普通莫队有一道模板题

https://www.luogu.org/problemnew/show/SP3267

 

代码：

#include
#define ll long long
#define ull unsigned long long
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 1010000;
int num[maxn], belong[maxn];// belong[ind] = id
int res[maxn];
int flag[maxn];
//flag用于记录当前区间数字出现次数       res:用于储存结果      belong[i] : 查询下标为i的数字属于哪一块
struct node {
	int l, r, id;
}q[maxn];
bool cmp(node a, node b) { //奇偶排序优化
	return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.rb.r);
	// 不处在同一块？ 按照左端点的块排序 ： （处在同一块那一块是奇数？ 按照右端点升序 ： 按照右端点降序   ）
}
int add(int num) {  
	if (flag[num] == 0) {
		flag[num]++;
		return 1;
	}
	flag[num]++;
	return 0;
}
int del(int num) {
	if (flag[num] == 1) {
		flag[num]--;
		return -1;
	}
	flag[num]--;
	return 0;
}
int main() {
	int n, m;
	memset(flag, 0, sizeof(flag));
	cin >> n;
	for (int i = 1; i <= n; i++) {
		scanf("%d", num + i);
	}
	double siz = sqrt(n);
	for (int i = 1; i <= n; i++) belong[i] = ceil(i / siz); // 分块的id
	cin >> m;
	for (int i = 1; i <= m; i++) {
		scanf("%d %d", &q[i].l, &q[i].r);
		q[i].id = i;
	}
	sort(q + 1, q + 1 + m, cmp);
	int l = 1, r = 0, sto = 0;
	for (int i = 1; i <= m; i++) { // l + 的时候 是 del
		while (l < q[i].l) sto += del(num[l++]); //这个点debug了很久
		while (l > q[i].l) sto += add(num[--l]);
		while (r > q[i].r) sto += del(num[r--]);
		while (r < q[i].r) sto += add(num[++r]);
		res[q[i].id] = sto;
	}
	for (int i = 1; i <= m; i++) printf("%d\n", res[i]);
	return 0;
}

 

带修莫队：

其实这个莫队还是只能解决离线问题，因为需要对询问区间排序，只能对所有询问排序后统一处理。

假如询问里面包含修改，那么我们要怎么做呢？

就是讲区间从二维变成三维，加入时间的纬度。

比如还是这道题：

给你n个数，q次操作，每次操作可以更改某一个值或者查询[l,r]区间内的最大值

n=5   这5个数分别是 1，2，3，4，5

q=3   3个操作分别是：

查询[2,4]区间最大值 操作记为q1

将第3个数改成7 操作记为q2

查询[2,4]区间的最大值 记为q3

 

对于每一个修改，我们将其定义为不同的时间，并且递增顺序增加，对于每一个查询，并不影响当前时间

假如q2的时间是1的话，那么q1的时间就是0，q3的时间就是1，并且记录时间为1的操作

 

当我们最后处理区间的时候

对于q1，当前时间为0，q1所在时间为0，时间一致

对于q2，当前时间为0，q2所在时间为1，时间不一样，执行时间为1的操作

 

题目：

https://www.luogu.org/problemnew/show/P1903

#include
using namespace std;
const int maxn = 5e4 + 7;
int num[maxn], belong[maxn], flag[1000007], res[maxn];
struct node1 {
	int l, r, id, pos;
}q[maxn];
struct node2 {
	int aim, to;
}r[maxn];
inline int read() {
	int x = 0, f = 1; register char ch = getchar();
	for (; ch<'0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
	for (; ch >= '0'&&ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
	return x * f;
}
inline bool cmp(node1 a ,node1 b) {
	return belong[a.l] ^ belong[b.l] ? belong[a.l] < belong[b.l] : (belong[a.r] ^ belong[b.r] ? belong[a.r] < belong[b.r] : a.pos < b.pos);
}
inline int add(int x) {
	if (++flag[x] == 1) return 1;
	return 0;
}
inline int del(int x) {
	if (--flag[x] == 0) return -1;
	else return 0;
}
inline int t(int i,int j) {  // i:修改索引  j：询问索引
	int ret = 0;
	if (r[i].aim >= q[j].l&&r[i].aim <= q[j].r) {//只有在里面才可以
		if (++flag[r[i].to] == 1) ret++;
		if (--flag[num[r[i].aim]] == 0) ret--;
	}
	swap(num[r[i].aim], r[i].to); //这次改过去的，回来需要改回来，因此直接交换
	return ret;
}
int ans;
int main() {
	int n, m;
	n = read(), m = read();
	for (register int i = 1; i <= n; i++)	num[i] = read();
	int qind, rind;
	qind = rind = 0;
	double siz = sqrt(n); //不一定是这个
	for (int i = 1; i <= n; i++) belong[i] = ceil(i / siz);
	for (int i = 1; i <= m; i++) {
		char inp[5];
		scanf("%s", inp);
		if (inp[0] == 'Q') {
			q[++qind].l = read();
			q[qind].r = read();
			q[qind].pos = rind;
			//q[qind].id = i;
			q[qind].id = qind;
		}
		else {
			r[++rind].aim = read();
			r[rind].to = read();
		}
	}
	sort(q + 1, q + 1 + qind, cmp);
	int l = 1, r = 0, sto = 0, time = 0;
	for (int i = 1; i <= qind; i++) {
		while (l < q[i].l) sto += del(num[l++]);
		while (l > q[i].l) sto += add(num[--l]);
		while (r < q[i].r) sto += add(num[++r]);
		while (r > q[i].r) sto += del(num[r--]);
		//while (time < q[i].pos) sto += t(time++, i);// 不是time++
		//while (time > q[i].pos) sto += t(--time, i);
		while (time < q[i].pos) sto += t(++time, i);// 不是time++
		while (time > q[i].pos) sto += t(time--, i);
		res[q[i].id] = sto;
	}
	for (register int i = 1; i <= qind; i++) printf("%d\n", res[i]);
	return 0;
}