数据结构-第三章栈和队列-课后习题1-10
第三章栈和队列-课后习题1-10
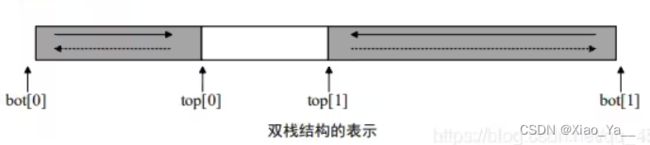
1.将编号为 0 和 1 的两个栈存放于一个数组空间 V[m]中,栈底分别处于数组的两端。当第0 号栈的栈顶指针 top[0]等于-1 时该栈为空;当第 1 号栈的栈顶指针 top[1]等于 m 时,该栈为空。两个栈均从两端向中间增长(见下图)。试编写双栈初始化,判断栈空、栈满、进栈和出栈等算法的函数。双栈数据结构的定义如下:
typedef struct
{
int top[2],bot[2];//栈顶和栈底指针
SElemType *V;//栈数组
int m;//栈最大可容纳元素个数
}DblStack;
1.算法描述【算法设计题】
Status InitStack(DblStack S)
{
//双栈初始化
S.V=new SElemType[m];
S.bot[0]=-1;
S.bot[1]=m;
S.top[0]=-1;
S.top[1]=m;
return OK;
}
int IsEmpty(DblStack S,int i)
{
//判断栈空
return S.bot[i]==S.top[i];
}
int IsFull(DblStack S)
{
//判断栈满
if(S.top[0]+1==S.top[1])
return 1;
else
return 0;
}
Status PushDblStack(DblStack &S,int i,SElemType e)
{
//进栈
if(S.top[0]+1==S.top[1])
return ERROR;
if(i==0)
S.V[++S.top[0]]=e;
else
S.V[--S.top[1]]=e;
return OK;
}
Status PopDblStack(DblStack &S,int i,SElemType &e)
{
//出栈
if(S.bot[i]==S.top[i])
return ERROR;
if(i==0)
e=S.V[S.top[0]--];
else
e=S.V[S.top[1]++];
return OK;
}
2.回文是指正读反读均相同的字符序列,如"abba"和"abdba"均是回文,但"good"不是回文。试写一个算法判定给定的字符向量是否为回文。(提示:将一半字符入栈)。
2.算法描述【算法设计题】
int IsPalindrome(chart *t)
{
InitStack(S);
len=strlen(t);
for(int i=0;i3.设从键盘输入一整数的序列:a1, a2, a3,…,an,试编写算法实现:用栈结构存储输入的整数,当ai≠-1时,将ai进栈;当ai=-1时,输出栈顶整数并出栈。算法应对异常情况(入栈满等)给出相应的信息。
3.算法描述【算法设计题】
//4.234 34+2*$
double PostFix()
{
InitStack(OPND);
num=0.0;
ch=getchar();
while(ch!='$')
{
i=0;
while((ch>='0')&&(ch<='9')||ch=='.')
{
data[i]=ch;
i++;
ch=getchar();
}
num=atof(data);
Push(OPND,num);
switch(ch)
{
case ' ':break;
case '+':Pop(OPND,b);Pop(OPND,a);Push(OPND,a+b);break;
case '-':Pop(OPND,b);Pop(OPND,a);Push(OPND,a-b);break;
case '*':Pop(OPND,b);Pop(OPND,a);Push(OPND,a*b);break;
case '/':Pop(OPND,b);Pop(OPND,a);Push(OPND,a/b);break;
}
ch=getchar();
}
return GetTop(OPND);
} 4.从键盘上输入一个后缀表达式,规定:后缀表达式长度不超过一行,以’$'结束操作数之间用空格分割。且操作符只有 + - * / 四种。
后缀表达式:234 34 + 2 *$。
4.算法描述【算法设计题】
void InOutS(int S[])
{
top=0;//top为栈顶指针,top=0时栈空
for(int i=0;i<=n;i++)
{
if(x!=-1)
{
if(top==maxsize-1)
{
cout<<"栈满"<5.假设以I和O分别表示入栈和出栈操作。栈的初态和终态均为空,入栈和出栈的操作序列可表示为仅由I和O组成的序列,称可以操作的序列为合法序列,否则称为非法序列。
5.算法描述【算法设计题】
//5.判定所给的操作序列是否合法
bool Judge(char A[])
{
i=0;
j=k=0;//j和k分别为I和字母O的个数
while(A[i]!='\0')
{
switch(A[i])
{
case 'I':j++;break;
case 'O':k++;
if(k>j)
{
cout<<"序列非法"<6.假设以带头结点的循环链表表示队列,并且只设一个指针指向队尾元素结点(注意不设头指针),试编写相应的队列初始化、入队和出队的算法。
6.算法描述【算法设计题】
//6.置空队列、判断队列是否为空、入队和出队
//队列的链式存储结构
typedef struct QNode
{
QElemType data;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct
{
QueuePtr rear;
}LinkQueue;
//置空队列
void InitQueue(LinkQueue &Q)
{
Q->rear=Q->rear->next;
while(Q->rear!=Q->rear->next)//当队列非空时,将队中元素逐个出队
{
S=Q->rear->next;
Q->rear->next=S->next;
delete S;
}
}
//判断队列是否为空,空返回1,否则返回0
int EmptyQueue(LinkQueue Q)
{
return Q->rear->next->next==Q.rear->next;
}
//入队,插入元素e为Q的新的队尾元素
Status EnQueue(LinkQueue &Q,QElemType e)
{
p=new QNode;
p->data=e;
p->next=Q->rear->next;
Q->rear->next=p;
Q->rear=p;
return OK;
}
//出队,删除Q的队头元素,用e返回其值
Status DeQueue(LinkQueue &Q,QElemType &e)
{
if(Q->rear->next->next==Q->rear->next)//队空
return ERROR;
p=Q->rear->next->next;//p指向队头元素
e=p->data;
if(p==Q->rear)
{
Q->rear=Q->rear->next;
Q->rear->next=p->next;
}
else
{
Q->rear->next->next=p->next;
}
delete q;
return OK;
} 7.假设以数组Q[m]存放循环队列中的元素,同时以rear和length分别指示环形队列中的队尾位置和队列中所含元素的个数。试给出该循环队列的队空条件和队满条件,并写 出相应的初始化(initqueue)、插入(enqueue)和删除(dlqueue)元素的操作。
7.算法描述【算法设计题】
//7.循环队列的插入和删除
typedef struct
{
ElemType *base;
int front,rear,tag;
}SqQueue;
//构造一个空队列
Status InitQueue(SqQueue &Q)
{
Q.base=new QElemType[M];
if(!Q.base) exit(OVERFLOW);
Q.front=Q.rear=0;
Q.tag=0;
return OK;
}
//插入元素e为Q的新的队尾元素
Status EnQueue(SqQueue &Q,QElemType e)
{
if((Q->tag==1)&&(Q->rear==Q->front))//队满
return ERROR;
Q.base[Q.rear]=e;
Q.rear=[Q.rear+1]%M;//队尾指针加1
if(Q->tag==0) Q->tag=1;//标志改1,表示队列非空
return OK;
}
//删除Q的队头元素,用e返回其值
Status DeQueue(SqQueue &Q,QElemType &e)
{
if((Q.tag==0)&&(Q.front==Q.rear))//队空
return ERROR;
e=Q.base[Q.front];
Q.front=[Q.front+1]%M;
if(Q->tag==1) Q->tag=0;
return OK;
} 8.如果允许在循环队列的两端都可以进行插入和删除操作。要求:
(1)写出循环队列的类型定义;
(2)写出“从队尾删除”和“从队头插入”的算法。
8.算法描述【算法设计题】
//8.在循环队列的两端进行插入和删除
typedef struct
{
QElemType *base;
int front;
int rear;
}SqQueue;
//在Q的队头插入新元素e
Status EnQueue(SqQueue &Q,QElemType e)
{
if(Q.rear==(Q.front-1+M)%M)//队满
return ERROR;
Q.base[Q.front]=e;
Q.front=(Q.front-1+M)%M;
return OK;
}
//删除Q的队尾元素,用e返回其值
Status DeQueue(SqQueue &Q,QElemType &e)
{
if(Q.front==Q.rear)//队空
return ERROR;
e=Q.base[Q.rear];
Q.rear=(Q.rear-1+M)%M;
return OK;
} 9.已知Ackermann函数定义如下: Ack(m,n)={n+1 当m=0时 Ack(m-1,1) 当m≠0,n=0时 Ack(m-1,Ack(m,n-1)) 当m≠0,n≠0时
(1)写出计算Ack(m,n)的递归算法,并根据此算法给出Ack(2,1)的计算过程。
(2)写出计算Ack(m,n)的非递归算法。
9.算法描述【算法设计题】
//9.Ack(m,n)的递归算法
int Ack(int m,n)
{
if(m==0)
return (n+1);
else if(m!=0&&n==0)
return (Ack(m-1,1));
else
return (Ack(m-1,Ack(m,n-1)));
}
//9.Ack(m,n)的非递归算法
int Ackerman(int m,int n)
{
for(j=0;j10.已知 f 为单链表的表头指针 , 链表中存储的都是整型数据,试写出实现下列运算的递归算法: 1 求链表中的最大整数; 2 求链表的结点个数; 3 求所有整数的平均值。
10.算法描述【算法设计题】
//10.递归求解链表的最大整数
int GetMax(LinkList p)
{
if(!p->next)//p指向表尾
return p->data;
else
{
int max=GetMax(p->next);
return p->data>=max?p->data:max;
}
}
//10.递归求解链表的结点个数
int GetLength(LinkList p)
{
if(!p->next)
return 1;
else
{
return GetLength(p->next)+1;
}
}
//10.递归求解链表中所有整数的平均值
double GetAverage(LinkList p,int n)
{
if(!p->next)
return p->data;
else
{
double ave=GetAverage(p->next,n-1);
//递归求解除尾结点之外的其余n-1个结点的平均值
return (ave*(n-1)+p->data)/n;
}
}