测量学1_测量学的基本知识
测量学
lesson 1:
测绘学的任务:
测绘学是以地球形状、大小及地球表面上各种地物的几何形状和地貌的形态为研究对象,研究如何将地面上的各种地物地貌测绘成图,同时将设计、规划在图纸上的各种建筑物放样于实地的有关理论与方法的一门科学。
测定(测绘)——由地面到图形
测设(放样)——由图形到地面
测定是使用测量仪器和工具,将测区内的地物和地貌的特征点的位置测量出来,按图式的要求缩绘成地形图,供规划设计、工程建设和国防建设使用。
测设是根据工程设计图纸上待建建筑物、构筑物的轴线位置、尺寸及其高程,算出其各特征点与控制点之间的距离、角度、高差等设计数据,然后以地面施工控制点为依据,将待建的建、构筑物的特征点在实地标定出来。
地物:地球表面的一切物体(包括自然地物和人工地物),如房屋、道路、桥梁等。
地貌:地表面自然形成高低起伏的连续形态,如山岭,溪谷,平原、河海等。
地形:地物和地貌总称为地形。
测绘学科的内容:
测绘学科是一级学科,其下有大地测量学、摄影测量学、遥感、全球卫星导航定位技术、工程测量学、地图制图学、地理信息系统等学科。
大地测量学:是一门研究和测定地球的形状、大小、重力场和地面点集合位置及其变化的理论和技术的学科。
工程测量学:在工程的规划设计,建设生产,管理运营三个阶段,应用测绘学的理论和方法,测定物体的大小,形状,位置的学科。包括控制测量、地形测绘、施工放样和变形监测。
地图制图学:是一门研究模拟地图和数字地图的基础理论、设计、变回、复制的技术方法的学科。主要包括地图投影、地图编制、地图整饰、地图制印等。
摄影测量学:是研究影像与被摄物体之间的内在的几何和物理关系,并对影像进行分析与解译,确定被摄物体的几何形状和位置,并判定其性质的一门学科。
遥感:通过非接触传感器(卫星,雷达)遥测物体的几何和物理特性的技术。
全球卫星导航定位技术:全球导航卫星系统是能在地球表面或近地空间的任何地点为用户提供全天候的3维坐标和速度以及时间信息的空基无线电导航定位系统。
地理信息系统:以采集、存储、管理、分析和描述整个或部分地球表面(包括大气层在内)与空间和地理分布有关的数据的空间信息系统。
地球的形状和大小:
地面上的点在地球上,地球表面是不规则的,有高山、盆地、河流和海洋等,是一个极不规则的曲面。
在地球上,一点处的重力是地球自转产生的离心力和地心引力的合力。
重力的方向线称为铅垂线,是测量工作的基准线(测量仪器对中整平就是基于铅垂线)。
水准面:静止的水面(有无数多个,是与重力方向垂直的连续曲面)。与水准面相切的平面成为水平面。
大地水准面:水准面中与平均海水面相吻合并向大陆、岛屿内延伸而形成的闭合曲面,称为大地水准面。(只有一个,由于各处地球重力不相等,所以是一个不规则曲面,是测量工作的基准面,大地水准面所包围的地球形体,称为大地体)。
在上述不规则曲面上确定点位和进行数据处理都非常困难,所以需要选择一个表面非常接近大地水准面,并且可用数学模型表达的几何形体来代替地球的几何形状,该几何形体成为地球椭球体(旋转椭球体),其表面是测量计算的基准面,椭球面法线是测量计算的基准线。
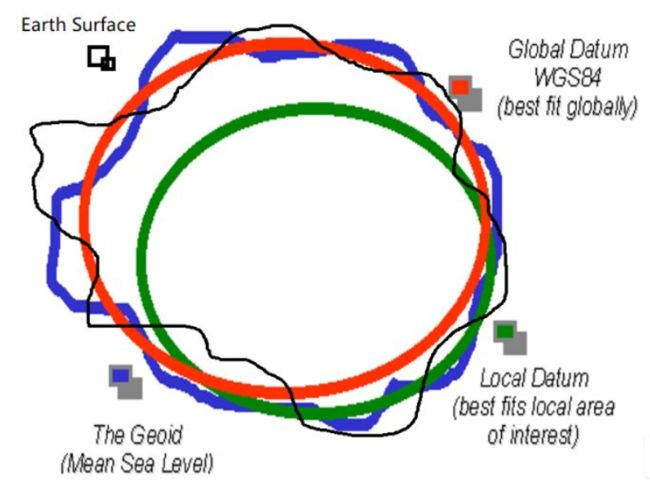
参考椭球:与某个区域,如一个国家大地水准面最为密合的椭球称为参考椭球。(1954北京坐标系,1980国家大地坐标系)
总地球椭球:参考椭球有许多个,而总地球椭球只有一个,是全球范围内大地水准面差距平方和最小的那个椭球面。(WGS84坐标系,2000国家大地坐标系)
区分:大地高,正高,正常高
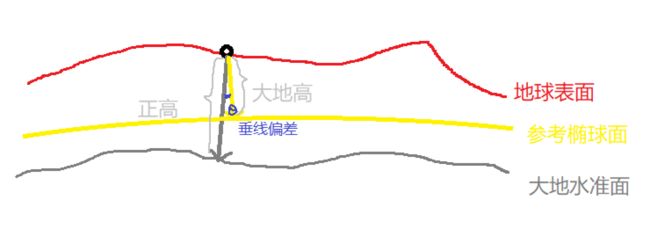
似大地水准面:是一个类似大地水准面的计算辅助面,既非数学面,亦非物理面(重力等位面),以其为参考面得到高程系统称正常高。我国采用正常高系统。
一点沿着椭球面法线到椭球面的距离称为大地高。
一点沿此处铅垂线(重力方向)到大地水准面的距离称为正高,一般亦称海拔高。
该椭球面法线与铅垂线夹角称为垂线偏差。
大地高与正高之差称为大地水准面差距,大地高与正常高之差称为高程异常。
椭球的定位与定向:
椭球三参数:
-
长半轴a
-
短半轴b
-
扁率f = (a - b) / a
椭球定位是指确定椭球中心的位置,可分为两类:局部定位和地心定位。局部定位要求在一定范围内椭球面与大地水准面有最佳的符合,而对椭球的中心位置无特殊要求;地心定位要求在全球范围内椭球面与大地水准面有最佳的符合,同时要求椭球中心与地球质心一致或最为接近。
椭球定向是指确定椭球旋转轴的方向,不论是局部定位还是地心定位,都应满足两个平行条件:
①椭球短轴平行于地球自转轴;
②大地起始子午面平行于天文起始子午面
地面点位的确定:
测量工作的基本任务之一就是确定地面点的空间位置。
描述一个点的空间位置,测量学中一般用平面坐标和高程来表示。
天文地理坐标:以大地水准面为基准面,以铅垂线为基准线,地面点沿铅垂线方向投影到大地水准面上的位置。
天文经度λ指该点处子午面与首子午面所夹的二面角,天文纬度φ是指该点的铅垂线与赤道面的夹角。用天文测量方法测定。
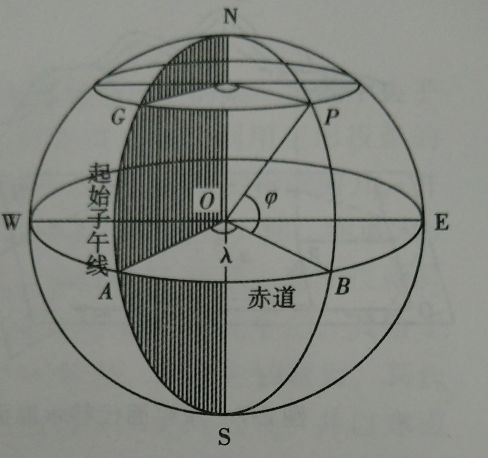
大地坐标系:把地面上的点沿着椭球面法线方向投影到椭球面上并用经纬度来表示其位置的坐标系叫大地坐标系。
地面点的大地经度(L)为通过该点的子午面与起始子午面(通过英国的Greenwich天文台)之间的夹角,由首子午面起算,向东0°~180°为东经,向西0°~180°为西经。
地面点的大地纬度(B)为通过该点的椭球面法线与赤道平面的交角,由赤道面起算,向北0°~90°为北纬,向南0°~90°为南纬。
大地高(H)为该点沿着椭球面法线到椭球面的距离,在椭球面之上为正,在椭球面之下为负。
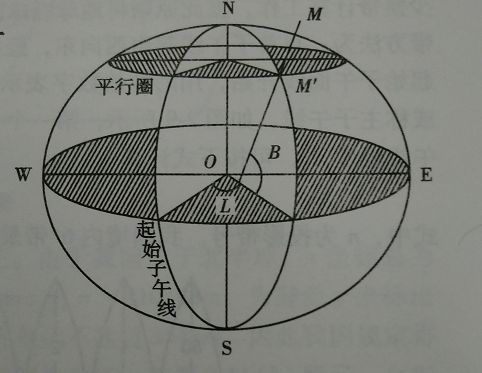
大地坐标正反算。
空间三维直角坐标系:以地球椭球的中心为原点,起始子午面与赤道面的交线为X轴,在赤道面通过原点与X轴垂直的为Y轴(右手系),地球椭球的旋转轴为Z轴。
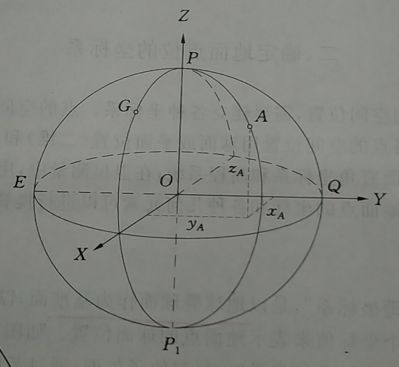
大地坐标与空间直角坐标的转换。
高斯平面直角坐标系:
在球面上计算不方便,我们一般是在平面上计算。可以采用地图投影的方法,将球面坐标转换为平面坐标。
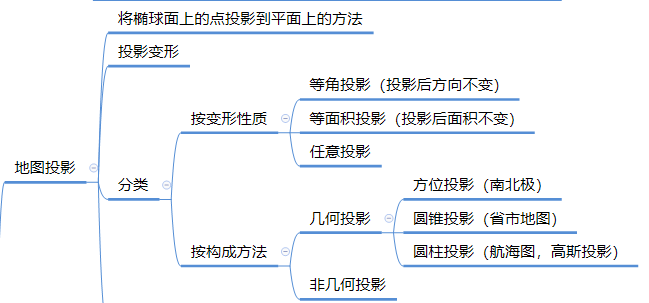
一般采用”高斯-克吕格投影“,所建立的平面直角坐标系称为“高斯平面直角坐标系”。
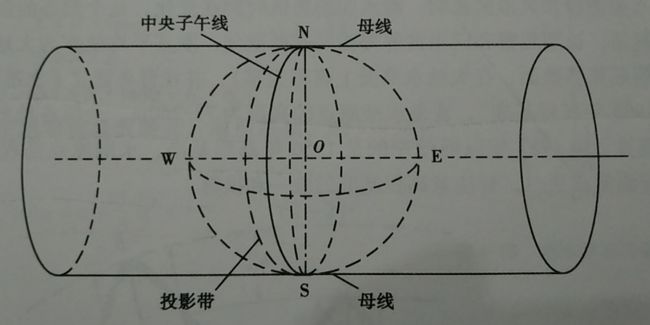
高斯投影的基本原理是:设想取一个椭圆柱面与地球椭球的某一中央子午线相切,在椭球面图形与柱面图形保持等角的条件下(称为“正形投影”),将球面图形投影在椭圆柱面上;然后将椭圆柱面沿着通过南、北极的母线切开,展开成平面。在这个平面上,中央子午线与赤道成为相互垂直相交的直线,分别作为高斯平面直角坐标系的纵轴(X和)和横(Y轴),在赤道上两轴的交点O作为坐标的原点建立高斯平面直角坐标系。
高斯投影分带:
按一定经差将地球椭球面划分为若干投影带,这是高斯投影中限制长度变形的最有效方法。
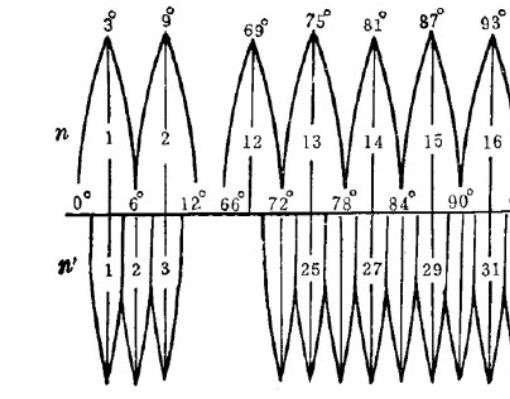
6度带,任意带的中央子午线经度 = 6n - 3,(我国位于13~23度带之间)计算带号公式为:n = int(经度/6) + (1)
3度带,任意带的中央子午线经度 = 3n,(我国位于24~45带之间)计算带号公式为:n = 经度/3(四舍五入)
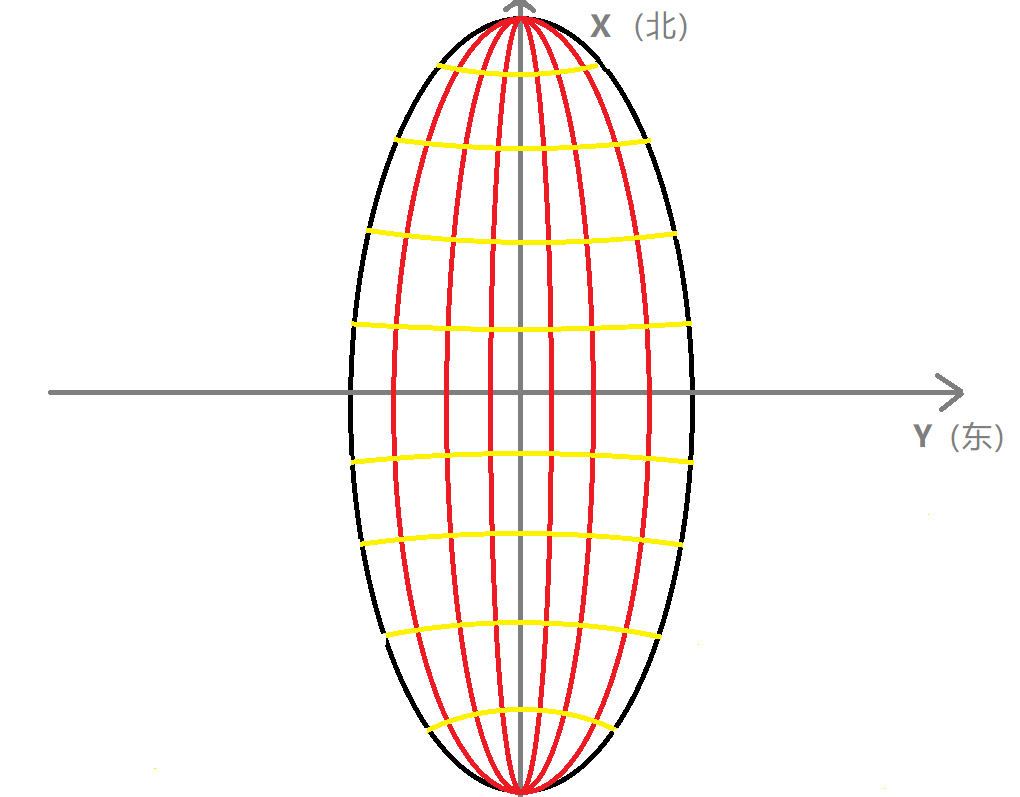
高斯投影是横轴椭圆柱等角投影,具有以下性质:
- 中央子午线投影后为一直线,无长度变形,其他子午线凹向中央子午线,离中央子午线越远变形越大
- 赤道投影后为一直线,其余纬线的投影为凸向赤道的曲线
- 经纬线投影后仍保持相互正交的关系,即投影后无角度变形
- 中央子午线和赤道的投影相互垂直
在高斯平面直角坐标系内,规定X轴向北为正,Y轴向东为正。位于北半球的国家,境内的X坐标值恒为正值,Y坐标值则有正有负。为避免坐标出现负值,将每个投影带的坐标原点向西移500km,则投影带中任一点的横坐标值也恒为正值。为了能确定某点在哪一个带内,在横坐标值前冠以带的编号。
在y坐标值上加了500km和带号后的横坐标称为通用值,没有加500km和带号的原横坐标值称为自然值。
高斯投影正反算、邻带换算。
独立平面直角坐标系:高斯平面直角坐标系离中央子午线越远,投影变形越大。所以城市的平面直角坐标系常常以城市中心地区某点的子午线作为中央子午线,据此进行高斯投影建立坐标系。
在小区域进行测量时,可以近似用水平面代替水准面,可以不考虑地图投影的问题。之后将坐标原点选在测区西南角,使坐标均为正值,地面点的位置就可以用平面直角坐标来表示。

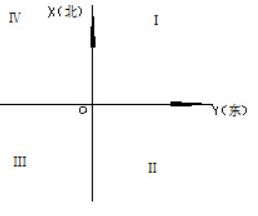
测量工作中采用的平面直角坐标系:南北方向为纵轴,记为x轴,向北为正,东西方向为横轴,记为y轴,向东为正。
测量上所采用的平面直角坐标系与数学上的基本相似,但坐标轴互换,象限编号顺序相反。
坐标正反算、平面直角坐标换算。
高程系统:
高程:地面点到大地水准面的铅垂距离,称为该点的绝对高程,或称海拔。
1956年黄海高程系统,水准原点72.289m;
1985高程系统,水准原点72.260m。
全国各地的高程都是以水准原点为基准进行推算的。
地面点到嘉定水准面的垂直距离为相对高程。
地面两点间的绝对或相对高程之差称为高差,用 h h h表示。 h A B = H B − H A h_{AB} = H_B - H_A hAB=HB−HA
测量工作概述:
测量的三个基本观测量:角度,距离,高差。
地面观测值------------>椭球面上-------------->高斯平面上-------------->计算
- 方向上做三差改正(垂线偏差、标高差、截面差),距离上进行改正,高差也需要进行改正。
- 方向改正、距离改正
要使总变形等于0,改变中央子午线经度或者改变椭球面高程(抵偿高程面)。
小区域进行测量时,可以近似用水平面代替水准面,但也有一个限度问题。
- 在10km的范围内,以水平面代替水准面对距离影响很小。
- 以水平面代替水准面,对高差影像显著(所以经常会有水准路线闭合差改正,正常水准面不平行改正等)。
- 在 100 k m 2 100km^2 100km2内,以水平面代替水准面对角度影响很小。
测量工作的基本原则:布局上“由总体到局部”,次序上“先控制后碎部”,精度上“由高级到低级”。并且步步有检核。