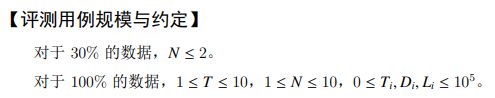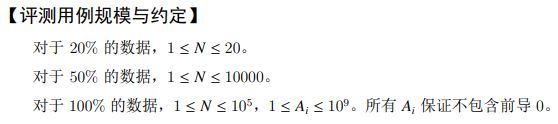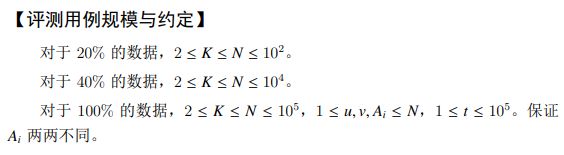可能有点错误,找到了再改(
A - 日期统计
将题面序列处理成数组放代码里
直接枚举八个位置的 \(O(n^8)\) 复杂度对于 \(n=100\) 的范围显然本地跑也跑不出来
但由于年份限制在 2023 年内,那么就找到所有为 2023 的子序列中,3 出现的最早的位置,记作 \(p\)
那么接下来花 \(O(n^4)\) 的时间枚举月份与日期所在位置,判断下即可
重复日期只算一次,故使用 set 去重
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
int a[100]={5,6,8,6,9,1,6,1,2,4,
9,1,9,8,2,3,6,4,7,7,
5,9,5,0,3,8,7,5,8,1,
5,8,6,1,8,3,0,3,7,9,
2,7,0,5,8,8,5,7,0,9,
9,1,9,4,4,6,8,6,3,3,
8,5,1,6,3,4,6,7,0,7,
8,2,7,6,8,9,5,6,5,6,
1,4,0,1,0,0,9,4,8,0,
9,1,2,8,5,0,2,5,3,3};
int cnt[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int main()
{
int flag=0,p;
repp(i,0,100)
{
if(flag==0&&a[i]==2)flag++;
else if(flag==1&&a[i]==0)flag++;
else if(flag==2&&a[i]==2)flag++;
else if(flag==3&&a[i]==3)flag++;
if(flag==4)
{
p=i;
break;
}
}
set st;
repp(x,p+1,100)
repp(y,x+1,100)
repp(z,y+1,100)
repp(u,z+1,100)
{
int m=a[x]*10+a[y];
int d=a[z]*10+a[u];
if(m>=1&&m<=12&&d>=1&&d<=cnt[m])
st.insert(m*100+d);
}
cout< B - 01 串的熵
根据题意,\(p(0)\) 表示字符 0 在整个字符串中数量的占比,同理 \(p(1)\) 表示字符 1 在整个字符串中数量的占比
由于两者与字符串实际上长什么样并没有关系,我们只需要知道字符串总长以及两种字符各自的数量即可
记 \(cnt_0\) 表示 0 的总数,\(cnt_1\) 表示 1 的总数,且 \(cnt_0+cnt_1=total=23333333\)
根据式子,总共有 \(cnt_0\) 项对熵的贡献是 \(-p(0)\log_2p(0)\),总共有 \(cnt_1=total-cnt_0\) 项对熵的贡献是 \(-p(1)\log_2p(1)\)
换句话说,熵就是 \(-cnt_0\cdot p(0)\log_2p(0)-cnt_1\cdot p(1)\log_2p(1)\)
枚举 \(cnt_0\) 从 \(0\) 到 \(\lfloor\frac{total}2\rfloor\),检查哪一项的值符合条件即可
时间复杂度 \(O(n)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
int main()
{
const double ans = 11625907.5798;
int total=23333333;
rep(i,0,total/2)
{
double c0=1.0*i/total;
double c1=1.0*(total-i)/total;
double s=-i*c0*log2(c0)-(total-i)*c1*log2(c1);
if(fabs(s-ans)<1e-4)
cout< C - 冶炼金属
假设答案为 \(k\),如果能用 \(a\) 份原料最多造出来 \(b\) 份成品,则应当满足:
- \(bk\le a \lt (b+1)k\)
对于左侧,移项得 \(k \le \frac a b\),可向下取整,得右边界为 \(\lfloor \frac a b \rfloor\)
对于右侧,移项得 \(k\gt \frac a {b+1}\),在 \(a\) 不是 \(b+1\) 的倍数的情况下应当向上取整,而在 \(a\) 是 \(b+1\) 倍数的倍数的情况下应当 \(+1\),得左边界为 \(\lfloor \frac a {b+1} \rfloor + 1\)
因此对于每条记录 \((a,b)\),可以得出答案区间为 \(\lfloor \frac a {b+1} \rfloor + 1 \sim \lfloor \frac a b \rfloor\)
对于多条记录,区间求交即可
时间复杂度 \(O(N)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
void solve()
{
int n;
cin>>n;
int mn=-1,mx=2e9;
rep(i,1,n)
{
int a,b;
cin>>a>>b;
mn=max(mn,a/(b+1)+1);
mx=min(mx,a/b);
}
cout< D - 飞机降落
发现 \(N=10\),考虑直接使用 next_permutation 或者 dfs 枚举所有可能的顺序即可
检查过程中,即上一架飞机降落后的时间为 \(mx\),则下一架飞机能够成功降落的条件为 \(mx\le T_i+D_i\),降落后的时间应当是 \(\max(mx,T_i)+L_i\)
时间复杂度 \(O(TN\times N!)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair pii;
int n,T[15],D[15],L[15];
int ord[15];
void solve()
{
cin>>n;
repp(i,0,n)
cin>>T[i]>>D[i]>>L[i];
repp(i,0,n)
ord[i]=i;
do
{
int mx=0;
bool flag=true;
repp(i,0,n)
{
if(mx>T[ord[i]]+D[ord[i]])
{
flag=false;
break;
}
mx=max(mx,T[ord[i]])+L[ord[i]];
}
if(flag)
{
cout<<"YES\n";
return;
}
}while(next_permutation(ord,ord+n));
cout<<"NO\n";
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
} E - 接龙数列
我们可以预先处理出第 \(i\) 个数的首位 \(L_i\) 及末位 \(R_i\),可以读入成字符串处理,也可以通过数位处理
考虑动态规划,记 \(dp[i]\) 表示在取第 \(i\) 个数当作接龙的最后一个数的前提下,第 \(1\) 个数到第 \(i\) 个数当中最长的接龙长度是多少
那么只需要按顺序处理,记一下 \(last[j]\) 表示最后一次出现末位为 \(j\) 的那个数在什么位置
转移方程便是 \(dp[i] = dp[last[L_i]] + 1\)
转移完成后更新一下 \(last[R_i]=i\) 即可
最后找一遍 \(dp\) 数组,取最大的值,答案便是 \(N-\max(\{dp\})\)
时间复杂度 \(O(N\log_{10} A_i)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
int n;
int L[100050],R[100050];
int dp[100050];
int last[100050];
void solve()
{
cin>>n;
rep(i,1,n)
{
int d; cin>>d;
R[i]=d%10;
while(d>9)
d/=10;
L[i]=d;
}
int mx=0;
rep(i,1,n)
{
dp[i]=dp[last[L[i]]]+1;
mx=max(mx,dp[i]);
if(dp[i]>dp[last[R[i]])
last[R[i]]=i;
}
cout< F - 岛屿个数
明显,通过搜索的方式实现找环、判点在环内太麻烦了
由于如果某个岛屿 \(b\) 完全包含在岛屿 \(a\) 内,那么 \(b\) 是不会统计到答案里的
因此我们只需要找有多少个岛屿能够接触到最外层的海水即可
不妨将整张图往外扩张一格,让最外层填充满海水,从最外层开始搜索,那么能够从海水中一步到达的岛屿一定是最外层的那些岛屿
需要注意的是,岛屿的环的判定是只有上下左右四个方向,样例中也能看出,例如下图是一个完整的环,内部的海水是不能被搜索的:
00000
01110
01010
01110
00000而下图不是一格完整的环,内部的海水是能被搜索到的,因此内部岛屿需要统计在答案中:
00000
00110
01010
01110
00000根据上面两个例子不难发现,我们在搜索海水的时候,是可以往八个方向搜的(即包含对角)
最后搜索出一些一定是外层岛屿上的位置后,遍历整张图再跑几遍搜索,找出总共有多少个连通块即可
时间复杂度 \(O(TMN)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef pair pii;
const int dx[8]={0,1,0,-1,-1,-1,1,1},dy[8]={1,0,-1,0,-1,1,-1,1};
int n,m;
char mp[55][55];
bool vis[55][55];
bool island[55][55];
inline bool prim(int x,int y)
{
return x>=0&&y>=0&&x<=n+1&&y<=m+1;
}
void bfs(int sx,int sy)
{
queue q;
q.push(pii(sx,sy));
vis[sx][sy]=true;
while(!q.empty())
{
pii p=q.front();
q.pop();
int x=p.first,y=p.second;
repp(i,0,4) // 四个方向
{
int px=x+dx[i],py=y+dy[i];
if(prim(px,py))
{
if(mp[px][py]=='1'&&!vis[px][py])
{
vis[px][py]=true;
q.push(pii(px,py));
}
}
}
}
}
void solve()
{
cin>>n>>m;
rep(i,1,n)
cin>>(mp[i]+1);
rep(i,0,n+1)
rep(j,0,m+1)
vis[i][j]=island[i][j]=false;
// 周围填海水
rep(i,0,n+1)
mp[i][0]=mp[i][m+1]='0';
rep(j,0,m+1)
mp[0][j]=mp[n+1][j]='0';
// 搜海水
queue q;
q.push(pii(0,0));
vis[0][0]=true;
while(!q.empty())
{
pii p=q.front();
q.pop();
int x=p.first,y=p.second;
repp(i,0,8) // 八个方向
{
int px=x+dx[i],py=y+dy[i];
if(prim(px,py))
{
if(mp[px][py]=='0')
{
if(!vis[px][py])
{
vis[px][py]=true;
q.push(pii(px,py));
}
}
else
island[px][py]=true;
}
}
}
// 搜岛屿
rep(i,0,n+1)
rep(j,0,m+1)
vis[i][j]=false;
int ans=0;
rep(i,1,n)
rep(j,1,m)
if(island[i][j]&&!vis[i][j]) // 如果是没有搜索过的外层岛屿
{
bfs(i,j);
ans++;
}
cout<>T; while(T--)
solve();
return 0;
} G - 子串简写
直接遍历,在遇到字符 \(b\) 时统计下 \(1\sim i-K+1\) 内有多少个字符 \(a\),加入答案即可
统计方面,遇到字符 \(a\) 时存下当前位置,只需二分找出最后一个符合条件的位置即可,时间复杂度 \(O(|S|\log |S|)\);或者直接前缀和,时间复杂度 \(O(|S|)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair pii;
void solve()
{
int k;
string s;
char a,b;
cin>>k>>s>>a>>b;
vector vec;
ll ans=0;
repp(i,0,s.size())
{
if(s[i]==b)
ans+=upper_bound(vec.begin(),vec.end(),i-k+1)-vec.begin();
if(s[i]==a)
vec.pb(i);
}
cout< H - 整数删除
记录每个点左侧是哪个位置,记作 \(L_i\),右侧是哪个位置,记作 \(R_i\),在删除之后更新一下左右两侧的相对位置
至于删除顺序,STL 维护下一个删除的元素,模拟 \(K\) 次即可
时间复杂度 \(O(N\log N)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef long long ll;
int n,k;
ll A[500050];
int L[500050],R[500050];
bool vis[500050];
struct node
{
ll val;
int pos;
node(){}
node(ll _val,int _pos)
{
val=_val;
pos=_pos;
}
bool operator < (const node& a) const
{
if(val!=a.val)
return val st;
void solve()
{
cin>>n>>k;
rep(i,1,n)
{
cin>>A[i];
L[i]=i-1;
R[i]=i+1;
st.insert(node(A[i],i));
}
rep(i,1,k)
{
node nd=*st.begin();
st.erase(st.begin());
int p=nd.pos;
if(L[p]!=0)
{
st.erase(st.find(node(A[L[p]],L[p])));
A[L[p]]+=A[p];
st.insert(node(A[L[p]],L[p]));
}
if(R[p]!=n+1)
{
st.erase(st.find(node(A[R[p]],R[p])));
A[R[p]]+=A[p];
st.insert(node(A[R[p]],R[p]));
}
// 更新左右两侧相对关系
int tl=L[p],tr=R[p];
L[tr]=tl;
R[tl]=tr;
vis[p]=true;
}
rep(i,1,n)
if(!vis[i])
cout< I - 景区导游
首先,对于每对 \((A_i,A_{i+1})\) 通过搜索将最短路找出来,在 \(N=K=10^5\) 的数据范围下是不现实的
但发现给定的图是一棵树,假如可以确定树根 \(rt\),那么树上两点 \((a,b)\) 之间距离也就等于 \(a\) 到 \(rt\) 的距离加上 \(b\) 到树根的距离减去两倍 \(lca(a,b)\) 到树根的距离,这里的 \(lca(a,b)\) 表示 \(a\) 与 \(b\) 两点的最近公共祖先
通过倍增的方法,可以在 \(O(\log N)\) 的时间复杂度内求出两点的 \(lca\)
因此我们可以计算得到按照 \(A_1,A_2,\cdots,A_K\) 的顺序走时的总距离 \(sum\)
但根据题意,对于 \(i=1\sim k\) 都需要求一遍当去除 \(A_i\) 这个点时的答案是多少,于是分以下三种情况讨论:
- \(i=1\),则从 \(sum\) 中减去 \(A_1\) 走到 \(A_2\) 的贡献;
- \(i=K\),则从 \(sum\) 中减去 \(A_{K-1}\) 走到 \(A_K\) 的贡献;
- \(i\in[2,k-1]\),则先从 \(sum\) 中减去 \(A_{i-1}\) 走到 \(A_i\) 的贡献,再减去 \(A_{i}\) 走到 \(A_{i+1}\) 的贡献,最后加上 \(A_{i-1}\) 走到 \(A_{i+1}\) 的贡献。
时间复杂度 \(O(N\log N)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair pii;
int n,k;
vector G[100050];
int A[100050],LCA[100050];
int dep[100050];
int fa[100050][18];
ll dis[100050];
void dfs(int u,int f)
{
fa[u][0]=f;
rep(i,1,17)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(pii &p:G[u])
{
int &v=p.first,&w=p.second;
if(v==f)
continue;
dep[v]=dep[u]+1;
dis[v]=dis[u]+w;
dfs(v,u);
}
}
int lca(int a,int b)
{
while(dep[a]>dep[b])
{
per(i,17,0)
if(dep[a]-(1<=dep[b])
a=fa[a][i];
}
while(dep[a]=dep[a])
b=fa[b][i];
}
if(a==b)
return a;
while(fa[a][0]!=fa[b][0])
{
per(i,17,0)
if(fa[a][i]!=fa[b][i])
{
a=fa[a][i];
b=fa[b][i];
}
}
return fa[a][0];
}
void solve()
{
cin>>n>>k;
repp(i,1,n)
{
int a,b,w;
cin>>a>>b>>w;
G[a].pb(pii(b,w));
G[b].pb(pii(a,w));
}
rep(i,1,k)
cin>>A[i];
dfs(1,0);
rep(i,2,k)
LCA[i]=lca(A[i-1],A[i]);
ll sum=0;
rep(i,2,k)
sum+=dis[A[i-1]]+dis[A[i]]-2*dis[LCA[i]];
rep(i,1,k)
{
ll tmp=sum;
if(i==1)
tmp-=dis[A[1]]+dis[A[2]]-2*dis[LCA[2]];
else if(i==k)
tmp-=dis[A[k-1]]+dis[A[k]]-2*dis[LCA[k]];
else
{
tmp-=dis[A[i-1]]+dis[A[i]]-2*dis[LCA[i]];
tmp-=dis[A[i]]+dis[A[i+1]]-2*dis[LCA[i+1]];
tmp+=dis[A[i-1]]+dis[A[i+1]]-2*dis[lca(A[i-1],A[i+1])];
}
cout< J - 砍树
可以将题意转换成,对于所有的 \(m\) 对给定的点对 \((a,b)\),如果都从 \(a\) 走到 \(b\),哪条边被走过了 \(m\) 次,多条边则取编号最大的一条
但本题统计的是边走过的次数,因此将边权转化为点权,以 \(1\) 为根时,其它所有点的点权都代表着连接自己与父亲的那条边走过的次数
对于从 \(a\) 走到 \(b\) 的路径上的标记,考虑采用树上差分,在 \(a\) 所在位置 \(+1\),在 \(b\) 所在位置 \(+1\),在 \(lca(a,b)\) 所在位置 \(-2\),最后从叶子向树根求和来算出每个点的点权,这里的 \(lca(a,b)\) 表示 \(a\) 与 \(b\) 两点的最近公共祖先,通过倍增实现
搜索时记录下每条边的编号是多少,把点权加到那个编号上,最后倒序找一遍那条边经过次数 \(=m\) 即可
时间复杂度 \(O(n\log n)\)
#include
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair pii;
int n,m;
vector G[100050];
int dep[100050];
int fa[100050][18];
int cha[100050];
int ans[100050];
void dfs(int u,int f)
{
fa[u][0]=f;
rep(i,1,17)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(pii &p:G[u])
{
int &v=p.first,&w=p.second;
if(v==f)
continue;
dep[v]=dep[u]+1;
dfs(v,u);
}
}
int lca(int a,int b)
{
while(dep[a]>dep[b])
{
per(i,17,0)
if(dep[a]-(1<=dep[b])
a=fa[a][i];
}
while(dep[a]=dep[a])
b=fa[b][i];
}
if(a==b)
return a;
while(fa[a][0]!=fa[b][0])
{
per(i,17,0)
if(fa[a][i]!=fa[b][i])
{
a=fa[a][i];
b=fa[b][i];
}
}
return fa[a][0];
}
void dfs2(int u,int f)
{
for(pii &p:G[u])
{
int &v=p.first,&id=p.second;
if(v==f)
continue;
dfs2(v,u); // 子树搜索完后再往上传,处理答案
cha[u]+=cha[v];
ans[id]=cha[v];
}
}
void solve()
{
cin>>n>>m;
repp(i,1,n)
{
int a,b;
cin>>a>>b;
G[a].pb(pii(b,i));
G[b].pb(pii(a,i));
}
dfs(1,0);
rep(i,1,m)
{
int a,b;
cin>>a>>b;
cha[a]++;
cha[b]++;
cha[lca(a,b)]-=2;
}
dfs2(1,0);
per(i,n-1,1)
{
if(ans[i]==m)
{
cout<