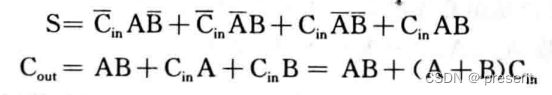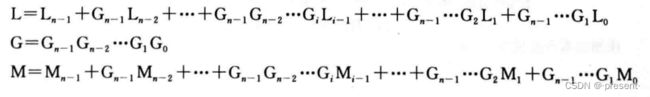常用组合逻辑电路及MSI组合电路模板的应用——下篇

一.加法器

计算机诞生的起因便是计算导弹轨道，因此计算是必经之路.

如何实现两个二进制数的相加呢？

在C语言操作符一节中，我们曾经利用与运算和异或运算，加上循环移位，实现了两个二进制数的

相加.

之所以可以实现，是因为异或运算可以实现没有进位的加法.与运算+移位则可以输出对应位的进

位.

而实际上，我们的加法器实现也是采取类似的思路.

先实现一位的加法和进位，再把它们通过不同方式串起来即可.

1.一位加法器

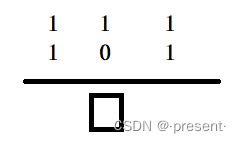
对于一个二进制数来说，比如方框输出的这一位，并不简简单单是对应位数的相加，不是1和0相

加，就可以得到，还需要考虑来自低位的进位，也就是1，三者加起来才是，最后的输出.

 如果考虑低位进位的一位二进制加法器，我们称之为全加器，反之，我们称之为半加器.

1.1半加器

只考虑本位两个一位二进制A和B相加，而不考虑低位进位的加法，称为半加.

我们可以很轻松写出其真值表.

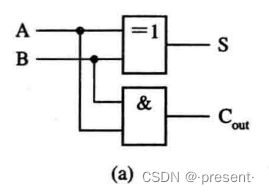
其中S代表的是直接相加的结果，用异或实现

     Cout代表的是进位输出的结果，用逻辑与实现

1.2全加器

前面也提到过了，一个位数的输出，往往还需考虑来自低位的进位.

将本位两个一位二进制数和来自低位的进位相加，叫做全加，具有全加功能的电路称为全加器.

通过找对应输出为1，可以写出对应的与或表达式，画出卡诺图，看一下，能否进一步化简，这里

就不再多解释，直接给出化简后的结果.

 我们看一下S输出，这个表达式是否有什么具体含义呢？

实际上，它代表总共有四种情况会得到输出为1，A为1(B为0，进位为0)或B为1(A为0，进位为0)或

进位为1(A为0，B为0),或者三者全为1，这其实很好理解.

那我们看一下Cout输出，这个表达式又是否有什么具体含义呢？

我们先看后一项，要想A + B输出为1，则A,B中至少有一个为1，那我们可以直接用AB + A + B来实

现Cout吗?显然还不可以，必须排除掉三者中只有一个为1的情况，所以我们将(A + B)和Cin用逻辑

与连接起来.

 

自己代入算一下，就可以发现，(A + B)Cin实际上实现了，除了A,B都为1，Cin为0，输出也要为1

的所有输出为1的情况.（A为1，B为0，Cin为1；A为0，B为1，Cin为1；A,B,Cin三者都为1）

最后我们再逻辑或上AB，也就补充上A,B都为1这种情况.

即每一位的进位输出，其实是有规律可循的，可以通过当前位，和后一位的进位来得到.

2.多位加法器

实现两个多位二进制相加的电路称为多位加法器.

2.1串行进位加法器

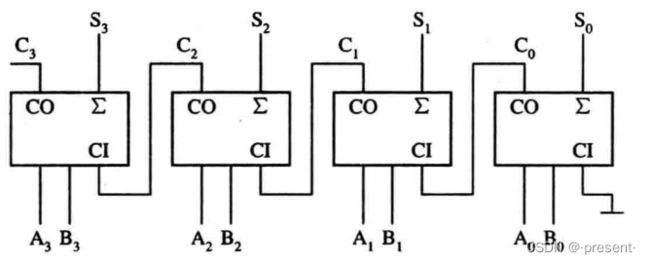
n位串行进位加法器由n个一位加法器串联而成.它具体如何实现，我们也可以大概猜想的到.

有了一位全加器，把低位的输出进位，当作Cin,输入到高位，由低到高计算即可.

这样的电路虽然结构简单，但却有着一个巨大的缺陷——运算速度慢.

每一高位的相加都必须等待低位的进位.假设一个n位加法器采用与非门来构造，总共延长时间是

3tp，则想要得到最后的正确结果，就必须等待n*3tp的时间，还要保证这段时间，并没有发生输入

的改变.

这显然不会很实用.

2.2超前进位加法器

为了提高运算速度，我们可以采取先计算好每一位的进位，保证每一位都能够同时完成运算，这样

就可以大大提升速度.

具体每一位的进位如何得到呢？

我们上面已经得到了进位的递推公式，有了递推公式，得到每一位的进位，其实不是问题，不断顺

着递归即可.

由递推公式，其实我们也可以知道，每个进位可以事先用不同位A0A1...,B0B1...计算得到.

当然，这样得到的组合逻辑电路就会相应复杂很多，而且位数越高，越复杂.

3.MSI 74283加法器

MSI 74283加法器是四位二进制超前进位加法器.

通过CI,CO两个端口，还可以实现构造八位二进制加法器.

将一个八位二进制数，从中间劈开，低位完成计算后，输出到高位，然后高位完成计算.

 

PS：一定要注意哪位接低位，哪位接高位，否则输出结果，可能不符合预期.

二.比较器

用来比较两个二进制数大小的逻辑电路，称为比较器.

1.一位比较器

一位比较总共有三种结果，要么Ai > Bi,Ai < Bi,Ai = Bi.

如果单纯用二个二进制位对应，其实就可以实现，毕竟二个二进制位就可以对应4种情况.

但为了电路设计方便为由，用了三个输出L,G,M来表示对应的三种情况，并且三种输出，有且只有

一个输出为1.输出有效为1，输出无效为0.

由真值表也可以得到下列的表达式.

其中我们知道，如果不满足L,M，那输出一定就为G，所以G的输出，其实就是L,M输出逻辑与后，

再取反. (也就是L,M都为0的时候，才取1)

2.多位比较器

多位比较器顾名思义，就是比较两个多位二进制数，从高位到低位依次进行比较，只有高位相等才

比较低位.

相关实现的逻辑表达式如下图所示. 

3.MSI 7485比较器

MSI 7485比较器是四位比较器.它的引脚图如下：

其中红色框中的是三个级联输入端，是为了在用这个芯片扩展成更高位比较器时而设的三个级联输

入端.

绿色框中就是输出的结果.

剩余的就是我们输入的二进制数，记住对应位置是从A3,B3开始比较，只有相等，才到A2,B2比较,

以此类推. 

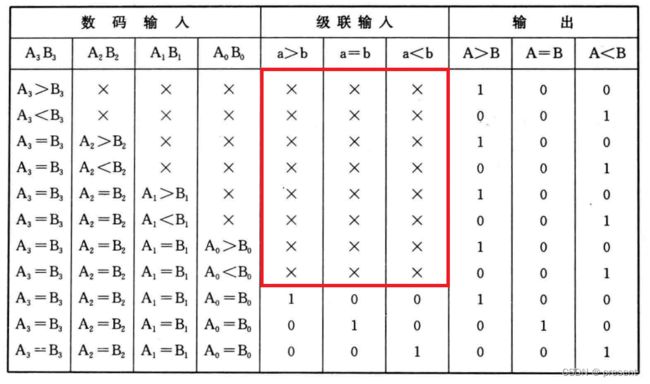
我们来看下MSI 7485比较器的真值表.

从中我们看到，如果两个比较的二进制数不相等，级联输入对输出是没有任何影响的. 

这也为我们利用两片7485构成八位二进制比较器奠定基础.

如果比较的是两个八位二进制数，我们可以从中割开

先比较高四位，这时候，低四位的级联输入对高四位的比较实际没有任何影响.

再比较低四位，这时候高四位相同，保证了低四位的输出，可以正确输出.

当然，为了最后可以判断两个八位二进制数可以相等，低位的级联输入一定要是0 1 0.

三.数据选择器 

输入给电视的数字信号有多组，通过遥控信号，也就是数据选择端，我们能够选择其中一个进行传

输.

能从多个数据输入中选择出其中一个进行传输的电路称为数据选择器.

抽象出来的框图如下，n个数据选择端，从2^n个数据输入端选择一个数据输出. 

1.介绍

我们来分析一个四选一数据选择器，先列出它的真值表.

总共6个输入端，2个为数据选择端，4个为数据输入端，当A1,A0都为0时，不管D3,D2,D1取什么

值,最后都会输出D0对应的值.

但这样的真值表，实际上会非常长，如果11个输入端(8+3)，那就需要列2^11，也就是2000多个

数，这显然不是我们想看到的. 

但我们仔细思索，抽象出之中的概念，我们可以发现，实际上可以把输入端，直接当作输出.

这反而还揭露了本质，对应数据选择端是什么，就可以得到相应的什么输出.

 我们可以根据这个真值表，写出对应表达式.

之所以能够写出这个表达式，是因为每个数据选择端，对应的只有一个输出Di，如果数据选择端此

时对应的是D0，那其它D1,D2,D3都等于0，也就相当于一个选择输入，对应一个最小项. 

2.MSI 74151数据选择器

MSI 74151数据选择器是一个互补输出的八选一的数据选择器.

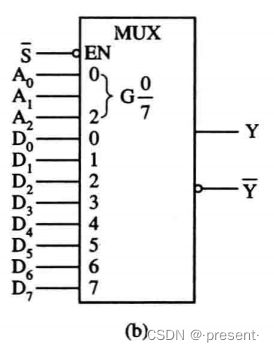
由下面图也可以看到，它有A2 A1 A0三个选择输入端，八个数据输入端

一个低电平有效的选通使能端.

两个输出端，有Y，也有.

下图，是其真值表.

3.用MSI数据选择器实现组合函数

逻辑函数可以写成最小项相或(相加)的形式.

而MSI数据选择器的逻辑表达式也包含所有数据输入端最小项的形式.

换句话说，我们也可以用数据选择器，类似译码器一样用它来实现任意一个组合函数.

在实现组合函数前，我们再思索一下

数据输入端究竟是什么？

举一个不太恰当的比喻，数据选择端就是站在舞台上的指挥家.而每一个数据输入端都是乐团的一

部分乐队的编号.

随着它值的改变，比如从0 0 1(A2 A1 A0)变化到0 1 0(A2 A1 A0)

对应的只有相应编码的乐团才会演奏.

那数据输入能否是一个变量呢？

答案是可以的.变量也是0和1的变化.

那数据选择端假设有三个端口，能否只使用两个端口呢？

答案也是可以的,对乐团的编码数目，完全取决于我们.

因此，可以分为下面三种情况进行讨论.

先写出逻辑函数F的标准与或表达式和数据选择器输出端的逻辑表达式.

一一进行比对，没有出现的项，对应数据输入端接0，出现的项，对应数据输入端接1.

并不需要任何额外器件.

这个时候不可能所有函数变量都充当数据选择端，因此有变量需要作为数据输入端，接入电路中.

要实现逻辑函数，还可能需要有反变量输入或其它门电路辅助.(一个组合函数还可能因为选择变量

作为不同数据选择端而有不同实现方式).

 先将变量接到数据选择器的m个数据选择端,再依据具体函数，来进一步确定剩下数据选择端和数

据输入端的值.

四.数据分配器

1.介绍

数据分配器，其实就是数据选择器的逆过来的部分.

它能根据选择信号的不同取值，将对应的信号，传送到对应的数据输出端.

下图为它的真值表

而实际上，若把D也看成是数据选择端中的一部分，那实际上，它就等同于我们前面学过的译码器.

当A1  A0分别为0 0时，A2 (D)可以取1或者0,都会只有唯一一个数据输出端，有对应数据输出.