Leetcode（239）——滑动窗口最大值

Leetcode（239）——滑动窗口最大值

题目

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：

示例 2：

输入：nums = [1], k = 1
输出：[1]

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104
• 1 <= k <= nums.length

题解

关键点：「随着窗口的移动实时维护最大值」——方法一和方法二

方法一：优先队列+延迟删除

思路

​​  对于维护「最大值」和「之前的最大值」，我们可以想到一种非常合适的数据结构和一种算法思想，那就是优先队列+延迟删除。其中的最大值优先队列可以帮助我们实时维护一系列元素中的最大值。类似 Leetcode 的第218题天际线。
​​  对于本题而言，初始时，我们将数组 $\text{nums}$ 的前 $k$ 个元素放入优先队列中。每当我们向右移动窗口时，我们就可以把一个新的元素放入优先队列中，此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中，在这种情况下，只需要判断这个最大值在数组 $\text{nums}$ 中的位置是否出现在滑动窗口左边界的左侧，是则是无效最大值，否则是有效最大值。因此，当我们后续继续向右移动窗口时，这个值就永远不可能出现在滑动窗口中了，我们可以将其永久地从优先队列中移除。
​​  我们不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系，我们可以在优先队列中存储二元组 $(\text{num},\text{index})$，表示元素 $\text{num}$ 在数组中的下标为 $\text{index}$。

代码实现

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<pair<int, int>> max;
        int head=0, tail=k-1, last=nums.size()-1;
        for(int n=0; n<k; n++){
            max.emplace(nums[n], n);
        }
        vector<int> ans{max.top().first};    // 存储答案
        while(tail != last){
            head++;
            tail++;
            max.emplace(nums[tail], tail);
            // 找到有效的最大值
            while(head > max.top().second){
                max.pop();
            }
            ans.push_back(max.top().first);
        }
        return ans;
    }
};

复杂度分析

时间复杂度：$O(n\log n)$ ，其中 $n$ 为数组的长度。该算法会遍历数组的每个数，为 $O(n)$，而在最坏情况下，数组 $\text{nums}$ 中的元素单调递增，那么最终优先队列中包含了所有元素，没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 $O(\log n)$，因此总时间复杂度为 $O(n\log n)$。
空间复杂度：$O(n)$ ，其中 $n$ 为数组的长度。即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 $O(n)$ 空间，只计算额外的空间使用。

方法二：单调队列

思路

​​  我们可以顺着方法一的思路继续进行优化某些操作——比如在方法一中每次窗口滑动时所需要的操作，即将一个元素放入优先队列操作的时间复杂度为 $O(\log n)$。
​​  我们可以考虑使用单调队列，来使每次窗口滑动时所需要的操作的时间复杂度优化为 $O(1)$——单调队列入队和出队的时间复杂度为 $O(1)$，进而实现算法的时间复杂度为 O(n)。

​​  关键点：

• 由于我们需要求出的是滑动窗口的最大值，如果当前的滑动窗口中有两个值在数组中对应的下标是 $i$ 和 $j$，其中 $i$ 在 $j$ 的左侧（$i<j$），并且 $i$ 对应的元素不大于 $j$ 对应的元素（$\text{nums}[i]\le \text{nums}[j]$），那么会发生什么呢？
• 当滑动窗口向右移动时，只要 $i$ 还在窗口中，那么 $j$ 一定也还在窗口中，这是 $i$ 在 $j$ 的左侧所保证的。因此，由于 $\text{nums}[j]$ 还存在于滑动窗口中，所以 $\text{nums}[i]$ 一定不会是滑动窗口中的最大值了（因为 $\text{nums}[i]$ 会比 $\text{nums}[j]$ 要先离开滑动窗口），此时可以将 $\text{nums}[i]$ 永久地移除。

​​  算法实现：

1. 因此我们可以使用一个双端队列存储所有还没有被移除的下标。在队列中，这些下标按照从小到大的顺序被存储，并且它们在数组 $\text{nums}$ 中对应的值是严格单调递减的，否则将被移除。
   因为如果队列中有两个相邻的下标，它们对应的值相等或者递增，那么令前者为 $i$，后者为 $j$，就对应了上面所说的情况—— $\text{nums}[i]$ 会被移除，这就与实际情况产生了矛盾。
2. 当滑动窗口向右移动时，我们需要把一个新的元素放入队列中。为了保持队列的性质，我们会不断地将新的元素与队尾的元素相比较，如果新的元素大于等于队尾的元素，那么队尾的元素就可以被永久地移除，我们将其从队尾弹出队列。我们需要不断地进行此项操作，直到队列为空或者新的元素小于队尾的元素。
3. 由于队列中下标在数组 $nums$ 中对应的值是严格单调递减的，因此队首下标对应的元素“可能”（需要判断）就是滑动窗口中的最大值。但与方法一中相同的是，此时的最大值可能在滑动窗口左边界的左侧，并且随着窗口向右移动，它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素，直到队首元素在窗口中为止。
4. 因此，算法中的单调队列的长度只需要等于 k （滑动窗口的长度） 即可。

举个例子： “543321” ，k=3

• 队列存值的情况下，如果不将两个3都加入，当第一个3被移出时，会导致321的最大值变为2，因为3已经被移出了，因此存值的话，需要新的元素大于队列尾部元素再去移除队列尾部的元素。
• 队列存下标的情况下，就可以只存一个3（存第二个），因为通过下标就能判断出移出的是第一个3还是第二个3。

例子：
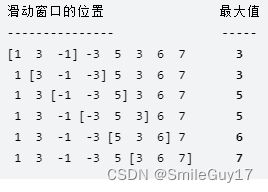
输入：nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出：[3,3,5,5,6,7]

解释过程中队列中都是具体的值，方便理解。
初始状态：L=R=0,队列：{}
i=0,nums[0]=1。队列为空,直接加入。队列：{1}
i=1,nums[1]=3。队尾值为1，3>1，弹出队尾值，加入3。队列：{3}
i=2,nums[2]=-1。队尾值为3，-1<3，直接加入。队列：{3,-1}。此时窗口已经形成，L=0，R=2，result=[3]
i=3,nums[3]=-3。队尾值为-1，-3<-1，直接加入。队列：{3,-1,-3}。队首3对应的下标为1，L=1，R=3，有效。result=[3,3]
i=4,nums[4]=5。队尾值为-3，5>-3，依次弹出后加入。队列：{5}。此时L=2，R=4，有效。result=[3,3,5]
i=5,nums[5]=3。队尾值为5，3<5，直接加入。队列：{5,3}。此时L=3，R=5，有效。result=[3,3,5,5]
i=6,nums[6]=6。队尾值为3，6>3，依次弹出后加入。队列：{6}。此时L=4，R=6，有效。result=[3,3,5,5,6]
i=7,nums[7]=7。队尾值为6，7>6，弹出队尾值后加入。队列：{7}。此时L=5，R=7，有效。result=[3,3,5,5,6,7]

代码实现

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> monotone_queue;  // 单调队列。存储下标，既方便取值，又方便判断是不是有效最大值
        // 准备阶段
        for(int n=0; n<k; n++){
            while(!monotone_queue.empty() && nums[monotone_queue.back()] <= nums[n])
                monotone_queue.pop_back();
            monotone_queue.push_back(n);
        }
        vector<int> ans{nums[monotone_queue.front()]};
        int length = nums.size(), n=k;
        while(n != length){
            // 插入新值
            while(!monotone_queue.empty() && nums[monotone_queue.back()] <= nums[n])
                monotone_queue.pop_back();
            monotone_queue.push_back(n);
            // 清理无效最大值
            while(!monotone_queue.empty() && monotone_queue.front() <= n-k)
                monotone_queue.pop_front();
			// 经历两个步骤（插入新值，清理无效最大值）后
			// 此时单调队列 monotone_queue.front() 中的就是滑动窗口右移后的新最大值的下标
            ans.push_back(nums[monotone_queue.front()]);
            n++;
        }
        return ans;
    }
};

复杂度分析

时间复杂度：$O(n)$，其中 $n$ 为数组 $\text{nums}$ 的长度。和方法一一样，每一个下标恰好被放入队列一次，并且最多被弹出队列一次，但是这次一个下标放入队列的时间复杂度为 $O(1)$，所以时间复杂度为 $O(n)$。
空间复杂度：$O(k)$，其中 $k$ 是滑动窗口大小。与方法一不同的是，在方法二中我们使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过 $k+1$ 个元素，因此队列使用的空间为 $O(k)$。这里所有的空间复杂度分析都不考虑返回的答案需要的 $O(n)$ 空间，只计算额外的空间使用。

方法三：分块 + 预处理

思路

​​  除了基于「随着窗口的移动实时维护最大值」的方法一以及方法二之外，我们还可以考虑其他有趣的做法。

​​  我们可以将数组 $\text{nums}$ 从左到右按照 $k$ 个一组进行分组，最后一组中元素的数量可能会不足 $k$ 个。如果我们希望求出 $\text{nums}[i]$ 到 $\text{nums}[i+k-1]$ 的最大值，就会有两种情况：

• 如果 $i$ 是 $k$ 的倍数，那么 $\text{nums}[i]$ 到 $\text{nums}[i+k-1]$ 恰好是一个分组。我们只要预处理出每个分组中的最大值，即可得到答案；
• 如果 $i$ 不是 $k$ 的倍数，那么 $\text{nums}[i]$ 到 $\text{nums}[i+k-1]$] 会跨越两个分组，占有第一个分组的后缀以及第二个分组的前缀。假设 $j$ 是 $k$ 的倍数，并且满足 $i<j\le i+k-1$，那么 $\text{nums}[i]$ 到 $\text{nums}[j-1]$ 就是第一个分组的后缀，$\text{nums}[j]$ 到 $\text{nums}[i+k-1]$ 就是第二个分组的前缀。如果我们能够预处理出每个分组中的前缀最大值以及后缀最大值，同样可以在 $O(1)$ 的时间得到答案。

算法实现：

因此我们用 $\text{prefixMax}[i]$ 表示下标 $i$ 对应的分组中，以 $i$ 结尾的前缀最大值；$\text{suffixMax}[i]$ 表示下标 $i$ 对应的分组中，以 $i$ 开始的后缀最大值。它们分别满足如下的递推式
$$\text{prefixMax}[i]=\{\begin{array}{ll}\text{nums}[i],& i是k的倍数\\ \max \{\text{prefixMax}[i-1],\text{nums}[i]\},& i不是k的倍数\end{array}$$​
以及
$$\text{suffixMax}[i]=\{\begin{array}{ll}\text{nums}[i],& i+1是k的倍数\\ \max \{\text{suffixMax}[i+1],\text{nums}[i]\},& i+1不是k的倍数\end{array}$$
需要注意在递推 $\text{suffixMax}[i]$ 时需要考虑到边界条件 $\text{suffixMax}[n-1]=\text{nums}[n-1]$，而在递推 $\text{prefixMax}[i]$ 时的边界条件 $\text{prefixMax}[0]=\text{nums}[0]$ 恰好包含在递推式的第一种情况中，因此无需特殊考虑。

在预处理完成之后，对于 $\text{nums}[i]$ 到 $\text{nums}[i+k-1]$ 的所有元素，如果 $i$ 不是 $k$ 的倍数，那么窗口中的最大值为 $\text{suffixMax}[i]$ 与 $\text{prefixMax}[i+k-1]$ 中的较大值；如果 $i$ 是 $k$ 的倍数，那么此时窗口恰好对应一整个分组，$\text{suffixMax}[i]$ 和 $\text{prefixMax}[i+k-1]$ 都等于分组中的最大值，因此无论窗口属于哪一种情况，
$$\max \{\text{suffixMax}[i],\text{prefixMax}[i+k-1]\}$$
即为答案。
这种方法与稀疏表（Sparse Table）非常类似，感兴趣的读者可以自行查阅资料进行学习。

代码实现

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> prefixMax(n), suffixMax(n);
        for (int i = 0; i < n; ++i) {
            if (i % k == 0) {
                prefixMax[i] = nums[i];
            }
            else {
                prefixMax[i] = max(prefixMax[i - 1], nums[i]);
            }
        }
        for (int i = n - 1; i >= 0; --i) {
            if (i == n - 1 || (i + 1) % k == 0) {
                suffixMax[i] = nums[i];
            }
            else {
                suffixMax[i] = max(suffixMax[i + 1], nums[i]);
            }
        }

        vector<int> ans;
        for (int i = 0; i <= n - k; ++i) {
            ans.push_back(max(suffixMax[i], prefixMax[i + k - 1]));
        }
        return ans;
    }
};

复杂度分析

时间复杂度：$O(n)$，其中 $n$ 为数组 $nums$ 的长度。我们需要 $O(n)$ 的时间预处理出数组 $\text{prefixMax}$， $\text{suffixMax}$ 和计算答案。
空间复杂度：$O(n)$，其中 $n$ 为存储 $\text{prefixMax}$ 和 $\text{suffixMax}$ 需要的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 $O(n)$ 空间，只计算额外的空间使用。

---

方法四：平衡二叉排序树

时间复杂度和空间复杂度都比前三个方法高

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        // 整数数组长为l，窗口长度为k，滑动窗口中的最大值有l-k+1个
        // 两个问题：1.更新滑动窗口的内容 2.维护滑动窗口的最大值
        // 1.用队列（C++ 的双端队列）保存滑动窗口的内容————————优化，不需要队列，使用数组下标来保持
        // 2.用 map 来维护滑动窗口的最大值———— pair<值,个数>
        map<int, int> max;          // pair<值,个数>
        int front = 0,back = k-1;   // 使用数组下标和输入数组来实现队列
        int l = nums.size();
        // 准备阶段
        for(int n = 0; n<k; n++){
            if(max.find(nums[n]) == max.end()){
                max.insert({nums[n], 1});    // 不存在该值
            }else max[nums[n]] += 1;
        }
        vector<int>  ans{max.crbegin()->first};

        int head,newone; // 用于保存队列的队首和下一个进队列的值
        while(back != l-1){
            head = nums[front];
            newone = nums[++back];
            if(max[head] == 1){
                max.erase(head);          // 该值只有一个，直接删除
            }else max[head] -= 1;   // 该值不止一个，递减

            if(max.find(newone) == max.end()){
                max.insert({newone, 1});    // 不存在该值
            }else max[newone] += 1;

            ans.push_back(max.crbegin()->first);
            front++;
        }
        return ans;
    }
};