位运算算法【1】
文章目录
- 面试题 01.01. 判定字符是否唯一
- 题目
- 算法原理
- 解法一:哈希表
- 解法二:位图
- 代码实现
- 268. 丢失的数字
- 题目
- 算法原理
- 解法一:哈希表
- 解法二:高斯求和
- 解法三:位运算(异或运算的运算律)
- 代码实现
面试题 01.01. 判定字符是否唯一
题目
题目链接:面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
0 <= len(s) <= 100s[i]仅包含小写字母- 如果你不使用额外的数据结构,会很加分。
算法原理
解法一:哈希表
这里直接用哈希表,我们遍历整个字符串,如果不在哈希表里面,将这个字符丢进去,如果在直接返回false即可,如果到末尾还没有,则返回true。
时间复杂度为O(N),由于全是小写字符,只想要创建一个hash[26]即可,空间复杂度为O(1)
解法二:位图
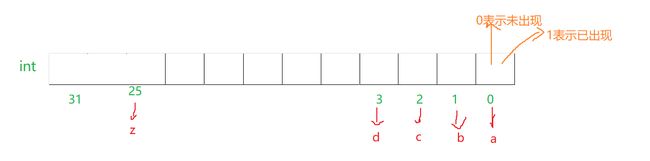
在解法一的基础上,我们还能继续优化一下,借助位图的比特位来标记信息
这样就能用一个int变量做到上面26个int变量做的的事情
在此基础上,还能继续优化一下,即鸽巢原理,由于小写的字符总共才26个,所有当这个字符串长度超过26的时候,必然有重复的
代码实现
class Solution {
public:
bool isUnique(string astr)
{
if(astr.size()>26) return false;
int bitMap = 0;
for(auto ch : astr)
{
int i = ch-'a'; //'a'的ASCII值为97
if((bitMap>>i)&1 == 1) return false;
bitMap |= 1<<i;
}
return true;
}
};
运行结果:
268. 丢失的数字
题目
题目链接:268. 丢失的数字 - 力扣(LeetCode)
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
提示:
n == nums.length1 <= n <= 1040 <= nums[i] <= nnums中的所有数字都 独一无二
**进阶:**你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?
算法原理
这里给的是[0,n],但是只给了n个,所以这个是缺少一个数字的。
解法一:哈希表
我们创建一个n+1大小的哈希表,从前往后遍历数组,然后看哪个数字没有被标记。
解法二:高斯求和
用数学公式求[0,n]的和,然后减去这个数组的和,即可得到缺少的数字,这个相比哈希表,空间复杂度为O(1)
ret = (0+n)*(n+1)/2 - sum[nums];
解法三:位运算(异或运算的运算律)
异或运算中有一个消消乐,相同的数字异或的结果为0,所以最后剩下的就是缺少的数字
代码实现
高斯求和:
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
int ret = (0+n)*(n+1)/2;
for(auto e:nums)
ret-=e;
return ret;
}
};
异或运算律:
class Solution {
public:
int missingNumber(vector<int>& nums) {
int ret = 0;
for(auto e:nums)
ret^=e;
for(int i=0;i<=nums.size();i++)
ret^=i;
return ret;
}
};
运行结果: