Leetcode——最长连续序列 / 最长递增子序列
1. 最长连续序列
(1)暴力
先对数组进行排序 这个很重要
之后再利用count变量储存连续的次数,如果和上一个不连续,就重置count 并把count的值保存到res变量中,最后返回res即可
注意:
- 如果没有连续的出现res的值会是0,但是比如 1 3 5 7 也可以看成他们的最大连续次数是1 ,所以最后进行了判断,返回res和count里面最大的一个
- 关于count为什么初始化为1 比如 1 2 3 4 从1开始到4结束会进行3次循环,count会加3次,不满足4,所以count初始化为1
- for循环是从1开始的,主要因为要判断当前的值和前一个的值是否相差1,如果从0开始要考虑越界问题
时间复杂度O(n)+O(nlogn)
空间复杂度O(1)
class Solution {
public int longestConsecutive(int[] nums) {
if (nums.length == 0 || nums == null) {
return 0;
}
Arrays.sort(nums);
int len=nums.length;
int count = 1;
int res=0;
for (int i = 1; i < len; i++) {
if (nums[i] == nums [i-1]) { //如果和上一个相同,直接跳过本次循环
continue;
}
if((nums[i] - nums[i-1]) == 1){
count++;
}else{
res=Math.max(count,res);
count=1;
}
}
return Math.max(res,count);
}
}
(2)Hash 优化
- 举nums中的每一个数x,并以x起点,在nums数组中查询x + 1,x + 2,,,x + y是否存在。假设查询到了 x + y,那么长度即为 y - x + 1,不断枚举更新答案即可。
- 如果每次查询一个数都要遍历一遍nums数组的话,时间复杂度为O(n) ,其实我们可以用一个哈希表来存贮数组中的数,这样查询的时间就能优化为O(1)
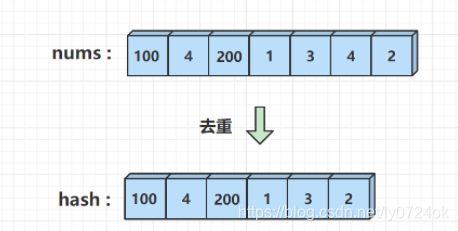
- 为了保证O(n)的时间复杂度,避免重复枚举一段序列,我们要从序列的起始数字向后枚举。也就是说如果有一个x, x+1, x+2, x+y的连续序列,我们只会以x为起点向后枚举,而不会从x+1,x+2,向后枚举。
具体过程如下:
- 1、定义一个哈希表hash,将nums数组中的数都放入哈希表中。
- 2、遍历哈希表hash,如果当前数x的前驱x-1不存在,我们就以当前数x为起点向后枚举。
- 3、假设最长枚举到了数y,那么连续序列长度即为y-x+1。
- 4、不断枚举更新答案。
O(n)
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> hash = new HashSet<Integer>();
for(int x : nums) //放入hash表中
hash.add(x);
int res = 0;
for(int x : hash)
{
if(!hash.contains(x-1))
{
int y = x; //以当前数x向后枚举
while(hash.contains(y + 1))
y++;
res = Math.max(res, y - x + 1); //更新答案
}
}
return res;
}
}
2. 最长递增子序列
(1)辅助数组
- 使用辅助数组来记录之前最长的递增子序列,当出现比之前的元素值还小的元素时,把之前的元素替换掉
- 这样,可以保证后面可以放入相对来说更小的元素,也就是让递增子序列增长得更缓慢一些,我们还是举个例子来详细解释一下。
- (这里是将比结果数组中更小的元素 替换到结果数组中,不会改变结果数组大小)
- 时间复杂度:O(n2),每个元素都要遍历一次,在 arr 数组中寻找花费不会超过 O(n),所以,总的时间复杂度是 O(n2)
- 空间复杂度:O(n),arr 数组需要占用 O(n)的额外空间。
比如,以 nums = [10,9,2,5,3,7,101,18] 为例,我们开辟一个数组 arr 大小与nums相同,同时声明一个变量 size 记录 arr 实际存储了多少个元素:
遍历到 nums[0] (10)时,arr 为空,直接放进去,arr = [10];
遍历到 nums[1](9)时,9 比 10 小,9 替换掉 10,arr = [9];
遍历到 nums[2](2)时,2 比 9 小,2 替换掉 9,arr = [2];
遍历到 nums[3](5)时,5 比 2 大,在后面累加,arr = [2, 5];
遍历到 nums[4](3)时,3 比 2 大,比 5 小,把 5 替换掉,arr = [2, 3],这样的话,后面如果有 4 ,是可以放在 3 后面的,也就是增长得更缓慢一些;
遍历到 nums[5](7)时,7 比 3 大,在后面累加,arr = [2, 3, 7];
遍历到 nums[6](101)时,101 比 7 大,在后面累加,arr = [2, 3, 7, 101];
遍历到 nums[7](18)时,18 比 7 大,比 101 小,把 101 替换掉,arr = [2, 3, 7, 18]。
最后,arr 的实际大小 size 就是我们求得的结果:最长递增子序列的长度。
class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len <= 1) {
return len;
}
int size = 1; // 表示arr数组实际的大小
int[] arr = new int[len];
arr[0] = nums[0]; // 初始化第0个元素
// 遍历nums中所有元素
for (int i = 1; i < len; i++) {
// 如果比arr最后一个元素大,直接在后面累加
if (nums[i] > arr[size - 1]) {
arr[size++] = nums[i];
} else {
// 否则的话,在arr中寻找它应该在的位置
// 即在arr中寻找大于等于它的元素的位置
int right = size - 1;
// 从后向前遍历找到这个位置
while (right >= 0 && arr[right] >= nums[i]) {
right--;
}
// 上面多减了一次,要补回来,使用更小的替换
arr[right + 1] = nums[i];
}
}
return size;
}
}
(2)辅助数组 + 二分法
把寻找位置的过程改成二分法而已,为什么可以使用二分法呢?
因为 arr 数组是递增的,天然适合使用二分法查找,代码如下:
- 时间复杂度:O(n log n),二分法查找的过程降到了 O(log n)。
- 空间复杂度:O(n),arr 数组需要占用 O(n)的额外空间。
class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len <= 1) {
return len;
}
int size = 1; // 表示arr数组实际的大小
int[] arr = new int[len];
arr[0] = nums[0]; // 初始化第0个元素
for (int i = 1; i < len; i++) {
if (nums[i] > arr[size - 1]) {
arr[size++] = nums[i];
} else {
// 利用二分法查找nums[i]在数组arr中的大于等于它的元素的位置
//左闭右开的二分
int left = 0, right = size;
while (left < right) {
int mid = (left + right) / 2;
if (arr[mid] >= nums[i]) {
right = mid;
} else {
left = mid + 1;
}
}
//这里是将比结果数组中更小的元素 替换到结果数组中,不会改变结果数组大小
//结果数组中符合条件的最小的
arr[left] = nums[i];
}
}
return size;
}
}
(3)记忆化搜索 (很慢)
- 使用深度优先搜索(DFS)是比较简单的,从每一个元素往下搜索它的最长递增子序列即可,但是,也是最慢的,所以,我们需要做一些优化。
- 假设 nums = [10,9,2,5,3,7,101,18],通过观察,可以发现,在寻找 2 的最长递增子序列的同时,3 的最长递增子序列也会顺带找出来,所以,我们可以在 DFS 的基础上加一个缓存,保存已经搜索过的元素,防止重复搜索,这也叫做 记忆化搜索。
class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len <= 1) {
return len;
}
int ans = 0;
int[] memo = new int[len];
//以每个元素为起点的最长递增子序列
for (int i = 0; i < len; i++) {
// 已经搜索过的直接跳过
if (memo[i] == 0) {
ans = Math.max(ans, dfs(nums, i, memo));
}
}
return ans;
}
private int dfs(int[] nums, int index, int[] memo) {
if (memo[index] != 0) {
return memo[index];
}
int ans = 0;
// 需要下探后面所有比当前元素大的元素
for (int i = index + 1; i < nums.length; i++) {
if (nums[i] > nums[index]) {
ans = Math.max(ans, dfs(nums, i, memo));
}
}
memo[index] = ++ans;
return ans;
}
}
(4)DP
有了记忆化搜索,我们转成动态规划就非常简单了,我们可以这样定义动态规划:

class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len <= 1) {
return len;
}
int ans = 0;
int[] dp = new int[len];
Arrays.fill(dp, 1); //初始化,仅一个单词的长度肯定为1
for (int i = 1; i < len; i++) {
// 遍历 i 之前的所有元素,看有没有比它小的,有就可以从它们转移过来
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1); // +1 表示加上当前节点本身的长度1
}
}
ans = Math.max(ans, dp[i]);
}
return ans;
}
}

