【数据挖掘】国科大刘莹老师数据挖掘课程作业 —— 第一次作业
homewrok 1
1. 假定数据仓库中包含 4 个维:date, product, vendor, location;和两个度量:sales_volume 和 sales_cost。
(a) 画出该数据仓库的星形模式
图 1 星形模式图
(b) 由基本方体 [date, product, vendor, location] 开始,列出每年在 Los Angles 的每个 vendor 的 sales_volume。
roll up on date from date_key to year
roll up on product from product_key to number
roll up on location from location_key to city
dice with 'city=Los Angles'
© 对于数据仓库,位图索引是有用的。以该立方体为例,简略讨论使用位图索引结构的优点和问题。
以 vendor 表中的 gender 和 marital_status 为例。假设前 4 个 vendor 的 gender 和 marital_status 取值如表 1 1 1 所示,gender 取值为 ”male“ 和 ”female“,marital_status 取值为 ”unmarried“,”married“ 和 ”divorce“,二者对应的 bitmap index 分别如表 2 2 2 和表 3 3 3 所示。
| row_id\attribution | gender | marital_status |
| 0 | male | divorce |
| 1 | female | unmarried |
| 2 | female | married |
| 3 | male | divorce |
表 1 前 4 个 vendor 对应的 gender 和 marital_status
| row_id\value | male | female |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
表 2 gender 对应的 bitmap indx
| row_id\value | unmarried | married | divorce |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
表 3 marital_status 对应的 bitmap indx
可见,gender 为 ”male“ 对应的索引值为 10,”female“ 对应的索引值为 01,marital_status 为 ”unmarried“ 对应的索引值为 100,”married“ 对应的索引值为 010,”divorce“ 对应的索引值为 001。
将两个 bitmap index 表(顺次)拼接后,0 号 vendor 对应的 index 为 10001,1 号 vendor 对应的 index 为 01100,2 号 vendor 对应的 index 为 01010,3 号 vendor 对应的 index 为 10001。
想要查询满足 gender=”female“ 且 martial_status=”unmarried“ 的 vendor,那么只需要让每个 vendor 对应的 index 与 01100 按位相与,结果仍然为 01100,说明该 vendor 满足条件。
优点:
bitmap indx 存储的是每一行数据是否满足一个条件,即用一个二进制位表示该条件是否成立。当需要查询数据满足某些条件时,可以将这些条件的 bitmap index 进行逻辑运算,从而快速得到结果。因此,bitmap index 可以大大提高查询效率。直观上,bitmap index 只存储二进制位,不存储具体的值。因此,它能够节省大量的存储空间,提高存储效率。
缺点:
① 适用场景有限:通过上面的例子可以看出,bitmap index 适用于表中取值为离散值的属性列,如果需要处理连续数据(比如,unit_price、ID_number 等),则需要先进行离散化处理,而离散化处理的质量依赖于离散化的粒度,可以想象到,离散粒度过大(粗),本质不同的区间可能被划分为同一类,离散粒度过小(细),划分的区间数过多,index 表出现稀疏问题,导致存储效率低下。因此,bitmap index 处理连续数据是比较困难的。另外,如果一个离散属性列的取值本来就很多,这会出现与对连续数据进行细粒度的离散化时相同的问题——存储效率低下。
② 更新开销较大:当 bitmap index 对应的属性列发生更新时,需要重新计算每个二进制位的值,这会引起一定的开销。特别是对于频繁更新的列,bitmap index 的维护成本会很高。因此,bitmap index 适用于静态数据。
2.假设一家医院对 18 名随机选择的成年人的年龄和体脂数据进行了测试,结果如下:
| id | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| age | 23 | 23 | 27 | 27 | 39 | 41 | 47 | 49 | 50 |
| %fat | 9.5 | 26.5 | 7.8 | 17.8 | 31.4 | 25.9 | 27.4 | 27.2 | 31.2 |
| id | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| age | 52 | 54 | 54 | 56 | 57 | 58 | 58 | 60 | 61 |
| %fat | 34.6 | 42.5 | 28.8 | 33.4 | 30.2 | 34.1 | 32.9 | 41.2 | 35.7 |
(a) 计算年龄和脂肪百分比的平均值、中位数和标准差。
保留四位小数结果如表 4 4 4 所示。
| mean | median | std | |
| age | 46.4444 | 51.0000 | 13.2186 |
| %fat | 28.7833 | 30.7000 | 9.2544 |
表 4 均值、中位数和标准差
(b) 绘制年龄和脂肪百分比的箱线图。
对于年龄,直接计算得到的最小值、上四分位数(Q1)、中位数、下四分位数(Q3)、最大值分别为:23、39.5、51、56.75、61。由于可能存在最大值超过 Q3+1.5×(Q3-Q1) 或者最小值不到 Q1-1.5×(Q3-Q1) 的情况,所以可能需要修正。经过测试,无需修正。
对于脂肪百分比,直接计算得到的最小值、上四分位数(Q1)、中位数、下四分位数(Q3)、最大值分别为:7.8、26.675、30.7、33.925、42.5。经过测试发现需要修正,修正后的最小值为 15.8。存在两个离群点(outlier)。
年龄和脂肪百分比的箱线图分别如图 2 2 2 左右所示。(需要注意代码封装的函数是以 1.25IQR 为标准,而老师的PPT是以 1.5IQR 为标准,所以下图右子图不准确)
图 2 箱线图
代码如下(仅以年龄数据为例):
import numpy as np
import matplotlib.pyplot as plt
x = [23, 23, 27, 27, 39, 41, 47, 49, 50, 52, 54, 54, 56, 57, 58, 58, 60, 61]
y = [9.5, 26.5, 7.8, 17.8, 31.4, 25.9, 27.4, 27.2, 31.2, 34.6, 42.5, 28.8, 33.4, 30.2, 34.1, 32.9, 41.2, 35.7]
x, y = np.array(x), np.array(y)
maximum = np.max(x)
minimum = np.min(x)
median = np.median(x)
Q1 = np.quantile(x, 0.25)
Q3 = np.quantile(x, 0.75)
IQR = Q3-Q1
print(f"最小值: {minimum}")
print(f"上四分位数: {Q1}")
print(f"中位数: {median}")
print(f"下四分位数: {Q3}")
print(f"最大值: {maximum}")
print(f"IQR: {IQR}")
print(f"修正后的最小值: {max(Q1-1.5*IQR, minimum)}")
print(f"修正后的最大值: {min(Q3+1.5*IQR, maximum)}")
plt.boxplot(x)
plt.show()
plt.plot()
补充:使用 np.quantile 函数的计算方法(interpolation 参数采用默认值 ‘linear’)。伪代码如下:
index = (len(a)-1) * p # a 为处理的序列,p 为百分比,如果获取 Q1,则 p=0.25 if index is integer: return a[index] else: index_below = floor(indedx) index_above = min(index_below + 1, len(a) - 1) weight_above = index - index_below weight_below = 1 - weight_above return a[index_below] * weight_below + a[index_above] * weight_above根据上面的伪代码可以计算出脂肪百分比的 Q1 = 26.5 × 0.75 + 27.2 × 0.25 = 26.675。
对于做题可以这样理解和记忆:Q1 对应第 ( N + 1 ) / 4 (N+1)/4 (N+1)/4 个位置的数(从 1 1 1 开始计数),如果不是整数,那么就是在该数下取整和加一下取整这两个位置之间,离得近的那一侧的位置对应的数分配更高的权重,远的一侧数分配小权重。比如计算得到的位置是 24.25 24.25 24.25,那么 Q1 为 0.75 0.75 0.75 乘以第 24 24 24 个数与 0.25 0.25 0.25 乘以第 25 25 25 个数之和。Q3 同理。
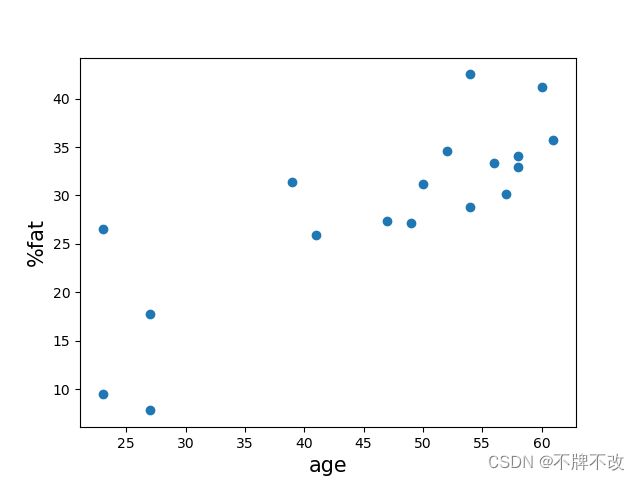
© 根据这两个变量绘制散点图。
以年龄为横坐标,以脂肪百分比为纵坐标绘制的散点图如图 3 3 3 所示。
图 3 散点图
对应代码如下:
import numpy as np
import matplotlib.pyplot as plt
x = [23, 23, 27, 27, 39, 41, 47, 49, 50, 52, 54, 54, 56, 57, 58, 58, 60, 61]
y = [9.5, 26.5, 7.8, 17.8, 31.4, 25.9, 27.4, 27.2, 31.2, 34.6, 42.5, 28.8, 33.4, 30.2, 34.1, 32.9, 41.2, 35.7]
x, y = np.array(x), np.array(y)
plt.xlabel('age', size=15)
plt.ylabel('%fat', size=15)
plt.scatter(x, y, )
plt.show()
(d) 基于”最小-最大归一化“对两个变量进行归一化。
保留四位小数结果如表 6 6 6 所示。
| id | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| age | 0.0000 | 0.0000 | 0.1053 | 0.1053 | 0.4211 | 0.4737 | 0.6316 | 0.6842 | 0.7105 |
| %fat | 0.0490 | 0.5389 | 0.0000 | 0.2882 | 0.6801 | 0.5216 | 0.5648 | 0.5591 | 0.6744 |
| id | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| age | 0.7632 | 0.8158 | 0.8158 | 0.8684 | 0.8947 | 0.9211 | 0.9211 | 0.9737 | 1.0000 |
| %fat | 0.7723 | 1.0000 | 0.6052 | 0.7378 | 0.6455 | 0.7579 | 0.7233 | 0.9625 | 0.8040 |
(e) 计算相关系数(Pearson’s product moment coefficient)。这两个变量是正相关还是负相关?
如果以总体数据计算,包括标准差和 Peason 相关系数,即
s t d = 1 n ∑ i = 1 n ( x i − x ˉ ) 2 r x , y = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) n σ x σ y \begin{align} {\rm std} &= \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i-\bar x)^2} \tag{1} \\ {\rm r}_{x,y} &= \frac{\sum_{i=1}^n(x_i- \bar x)(y_i - \bar y)}{n\sigma_x\sigma_y} \tag{2} \end{align} stdrx,y=n1i=1∑n(xi−xˉ)2=nσxσy∑i=1n(xi−xˉ)(yi−yˉ)(1)(2)
其中 σ \sigma σ 为标准差。保留四位的结果为 0.8176。
如果以样本数据计算,即
s t d = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 r x , y = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ( n − 1 ) σ x σ y \begin{align} {\rm std} &= \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i-\bar x)^2} \tag{3} \\ {\rm r}_{x,y} &= \frac{\sum_{i=1}^n(x_i- \bar x)(y_i - \bar y)}{(n-1)\sigma_x\sigma_y} \tag{4} \end{align} stdrx,y=n−11i=1∑n(xi−xˉ)2=(n−1)σxσy∑i=1n(xi−xˉ)(yi−yˉ)(3)(4)
保留四位的结果为 0.8657。
两种计算方法对应代码如下:
import numpy as np
x = [23, 23, 27, 27, 39, 41, 47, 49, 50, 52, 54, 54, 56, 57, 58, 58, 60, 61]
y = [9.5, 26.5, 7.8, 17.8, 31.4, 25.9, 27.4, 27.2, 31.2, 34.6, 42.5, 28.8, 33.4, 30.2, 34.1, 32.9, 41.2, 35.7]
x, y = np.array(x), np.array(y)
bar_x, bar_y = x.mean(), y.mean()
# std_x, std_y = x.std(ddof=1), y.std(ddof=1) # 样本标准差
std_x, std_y = x.std(), y.std() # 总体标准差
# r = np.sum((x - bar_x) * (y - bar_y)) / ((len(x)-1) * std_x * std_y) # 样本
r = np.sum((x - bar_x) * (y - bar_y)) / ((len(x)) * std_x * std_y) # 总体
print(r)
3.下面是一个超市某种商品连续 20 个月的销售数据(单位为百元)
| 21 | 16 | 19 | 24 | 27 | 23 | 22 | 21 | 20 | 17 | 16 | 20 | 23 | 22 | 18 | 24 | 26 | 25 | 20 | 26 |
对以上数据进行深度为 5 的 Equal-depth binning。
先排序!,排序后的序列为 {16,16,17,18,19,20,20,20,21,21,22,22,23,23,24,24,25,26,26,27}。
bin 1: 16, 16, 17, 18, 19
bin 2: 20, 20, 20, 21, 21
bin 3: 22, 22, 23, 23, 24
bin 4: 24, 25, 26, 26, 27
代码如下:
import numpy as np
x = [16,16,17,18,19,20,20,20,21,21,22,22,23,23,24,24,25,26,26,27]
x = np.array(x)
equal_depth_binning = np.array_split(x, [i for i in range(5, len(x), 5)])
print(equal_depth_binning)
(a) 采用 bin median 方法进行平滑。
bin 1: 17.2, 17.2, 17.2, 17.2, 17.2
bin 2: 20.4, 20.4, 20.4, 20.4, 20.4
bin 3: 20.8, 20.8, 20.8, 20.8, 20.8
bin 4: 25.6, 25.6, 25.6, 25.6, 25.6
bin_median_smooth = [np.round(i.mean(), 4) for i in equal_depth_binning]
print(bin_median_smooth)
(b) 采用 bin boundaries 方法进行平滑。
bin 1: 16, 16, 16, 19, 19
bin 2: 20, 20, 20, 21, 21
bin 3: 22, 22, 24, 24, 24
bin 4: 24, 24, 27, 27, 27
bin_boundaries_smooth = [np.max(chunk) if np.max(chunk) - i < i - np.min(chunk) else np.min(chunk) for chunk in equal_depth_binning for i in chunk]
print(bin_boundaries_smooth)