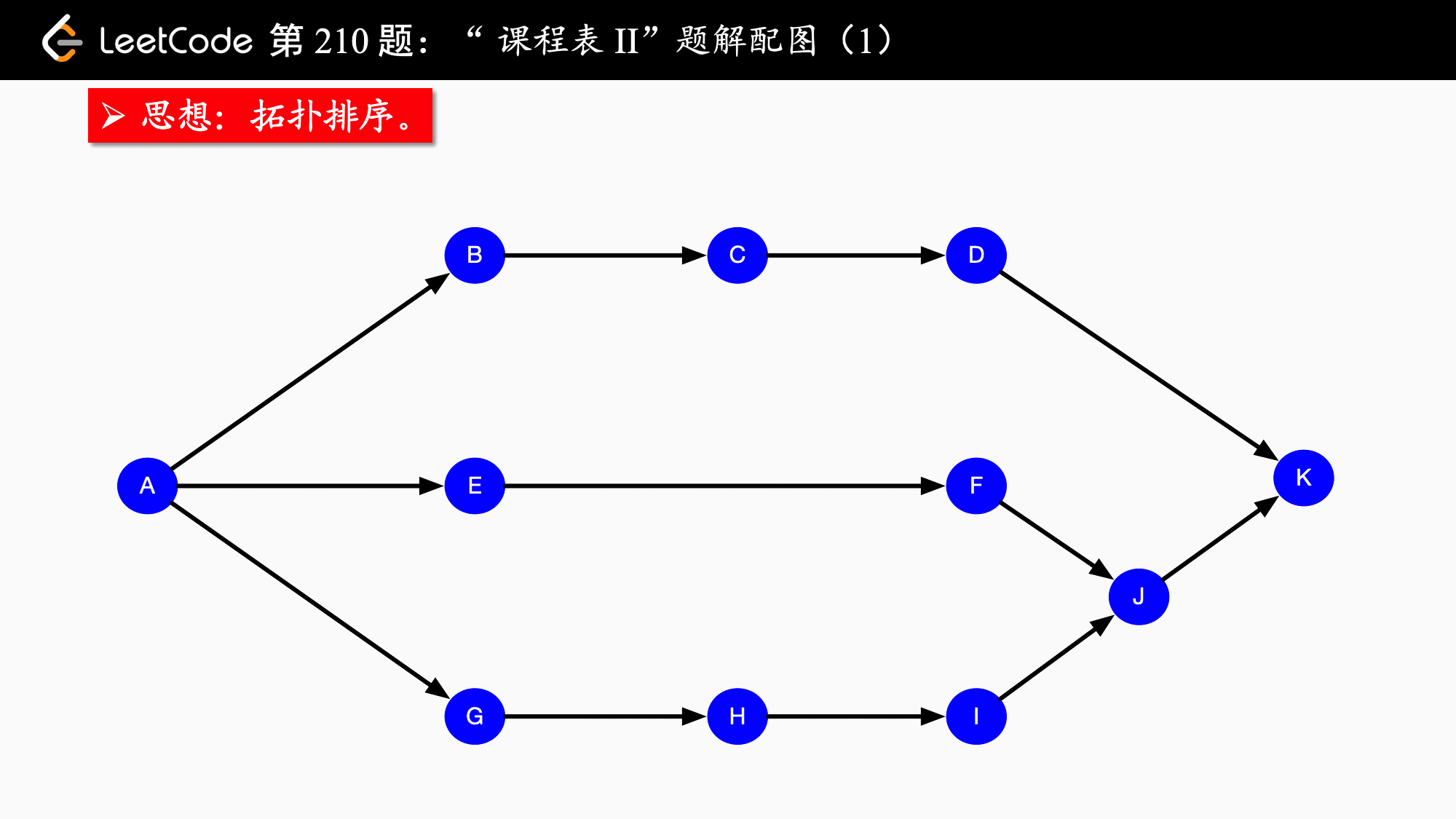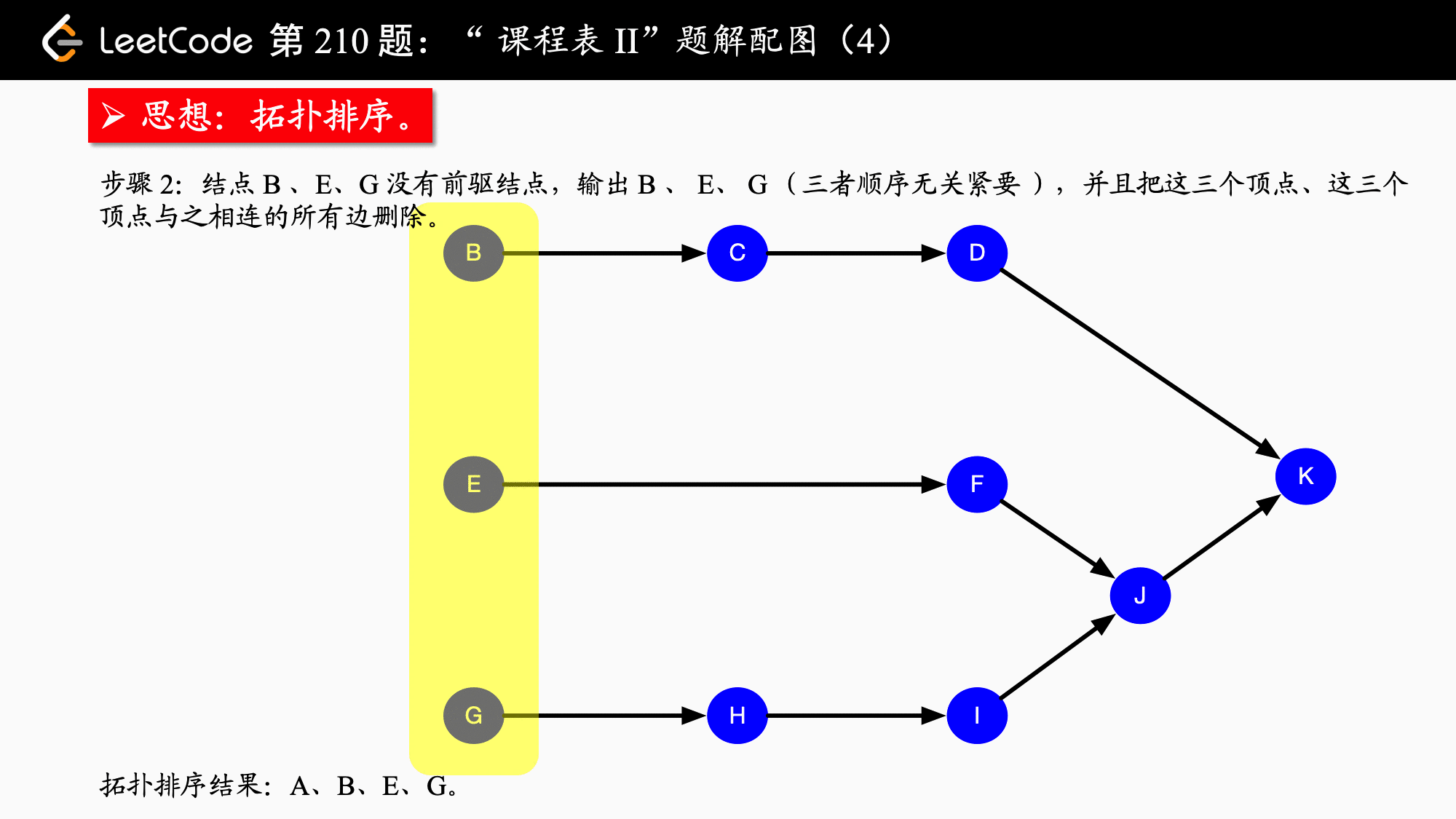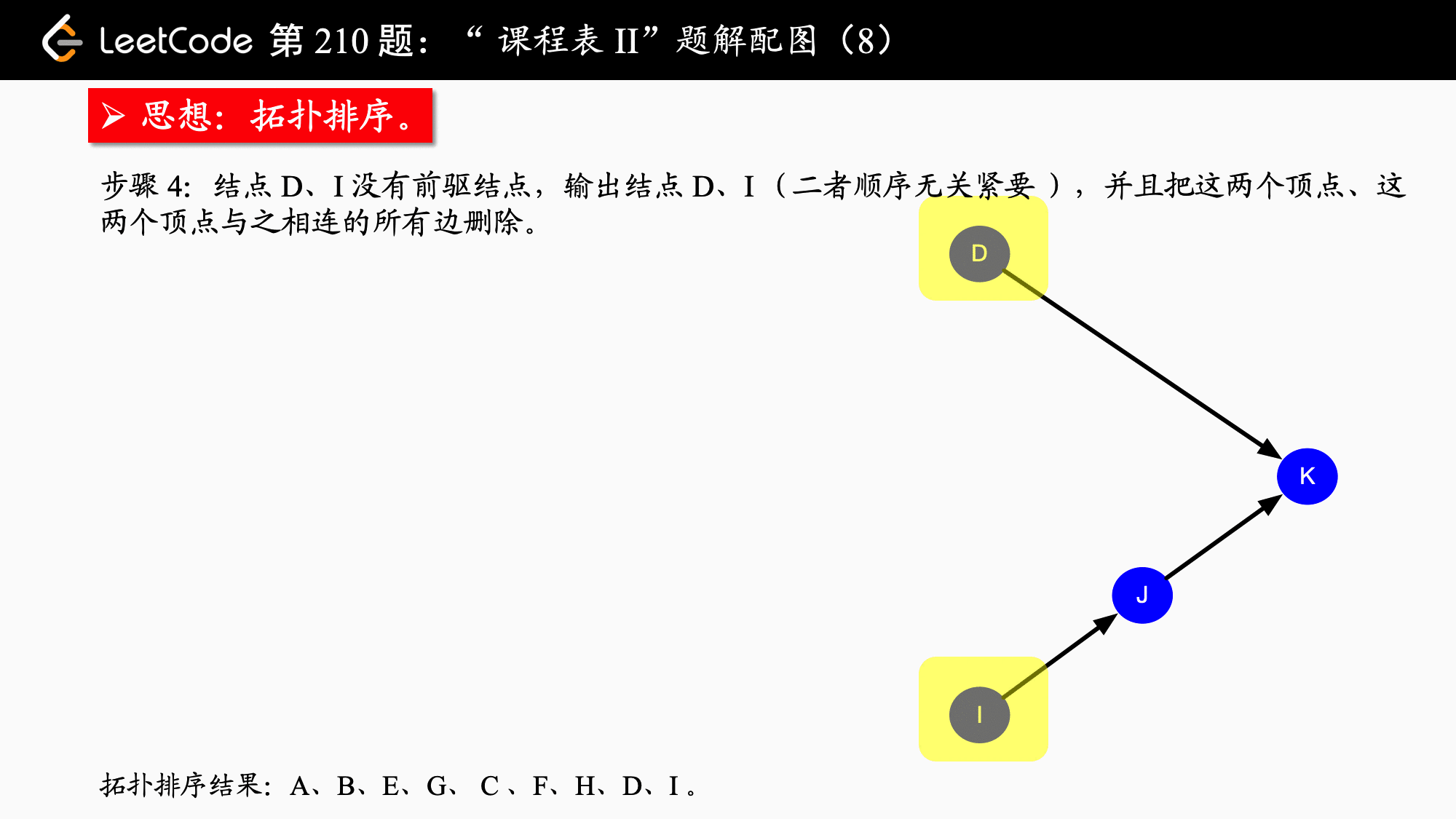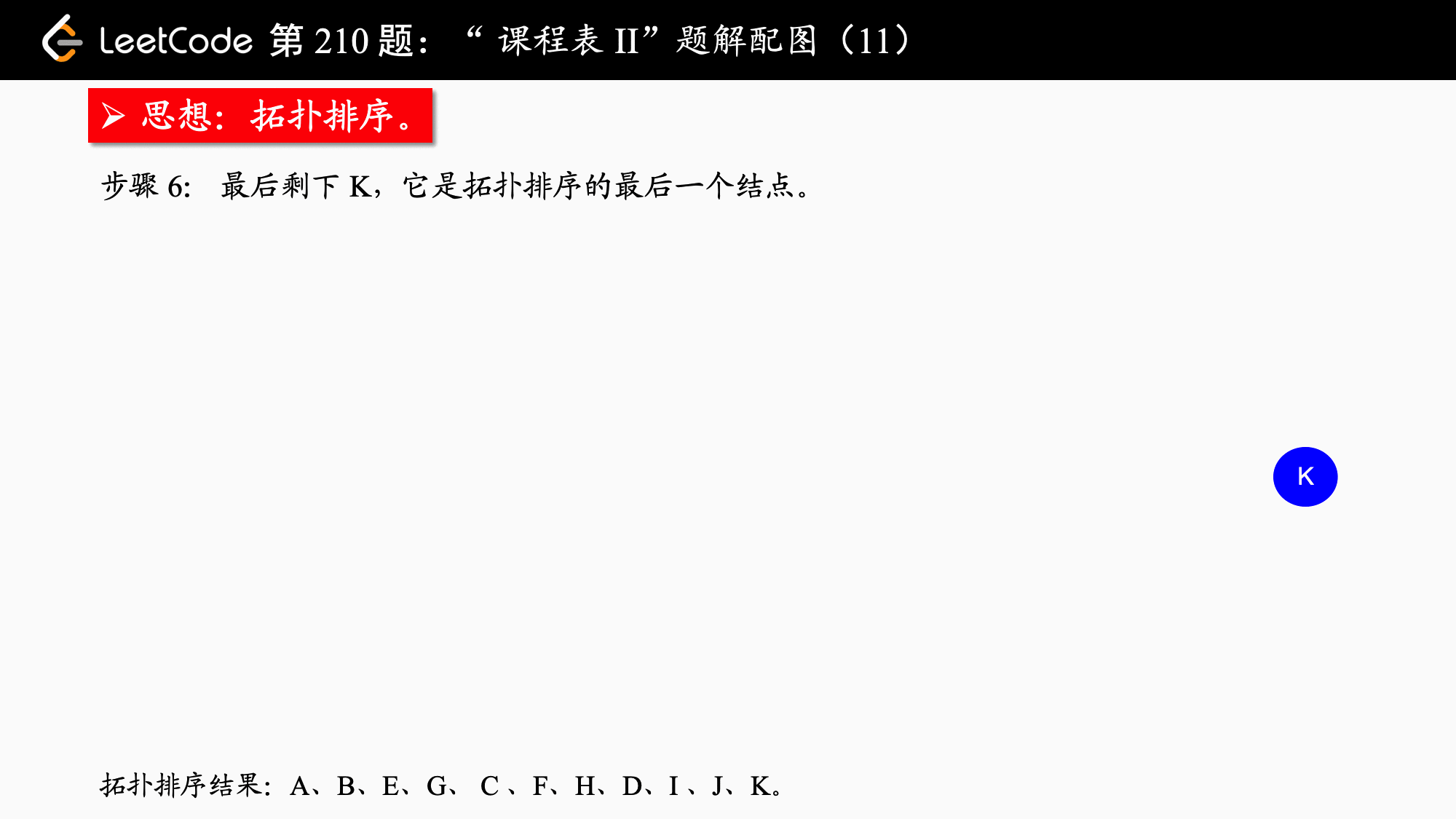
leetcode207.课程表、leetcode210.课程表 II、leetcode444.序列重建「拓扑排序」

目录

题目一：leetcode207.课程表

1.题目描述

2.解题思路

3.代码实现

题目二：leetcode210.课程表 II

1.题目描述

2.解题思路

3.代码实现

题目三：leetcode444.序列重建

1.题目描述

2.解题思路

3.代码实现

---

题目一：leetcode207.课程表

1.题目描述

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

输入: 2, [[1,0]] 
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。
示例 2:

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。
说明:

输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
提示:

这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。

2.解题思路

见下一题

3.代码实现

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """
        res = []
        indegree = [0 for _ in range(numCourses)]
        adj = [set() for _ in range(numCourses)]
        for sec, fir in prerequisites:
            indegree[sec] += 1
            adj[fir].add(sec)
        que=[]
        for i in range(numCourses):
            if indegree[i] == 0:
                que.append(i)
        while que:
            t = que.pop(0)
            res.append(t)
            for i in adj[t]:
                indegree[i] -= 1
                if indegree[i] == 0:
                    que.append(i)
        if len(res) == numCourses:
            return True
        else:
            return False

题目二：leetcode210.课程表 II

1.题目描述

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

示例 1:

输入: 2, [[1,0]] 
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
示例 2:

输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
     因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
说明:

输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
提示:

这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。

2.解题思路

参考：力扣

3.代码实现

class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: List[int]
        """
        res = []
        indegree = [0 for _ in range(numCourses)]
        adj = [set() for _ in range(numCourses)]
        for sec, fir in prerequisites:
            indegree[sec] += 1
            adj[fir].add(sec)
        que=[]
        for i in range(numCourses):
            if indegree[i] == 0:
                que.append(i)
        while que:
            t = que.pop(0)
            res.append(t)
            for i in adj[t]:
                indegree[i] -= 1
                if indegree[i] == 0:
                    que.append(i)
        if len(res) == numCourses:
            return res
        else:
            return []

题目三：leetcode444.序列重建

1.题目描述

验证原始的序列 org 是否可以从序列集 seqs 中唯一地重建。序列 org 是 1 到 n 整数的排列，其中 1 ≤ n ≤ 104 。重建是指在序列集 seqs 中构建最短的公共超序列。（即使得所有  seqs 中的序列都是该最短序列的子序列）。请你确定是否只可以从 seqs 重建唯一的序列，且该序列就是 org 。

示例 1：

输入：org = [1,2,3], seqs = [[1,2],[1,3]]
输出：false
解释：[1,2,3] 不是唯一的可重建序列，[1,3,2] 也是一个有效的可重建序列。
示例 2：

输入：org = [1,2,3], seqs = [[1,2]]
输出：false
解释：可重建序列只能是 [1,2] 。
示例 3：

输入：org = [1,2,3], seqs = [[1,2],[1,3],[2,3]]
输出：true
解释：序列 [1,2]、[1,3] 和 [2,3] 可以从原始序列 [1,2,3] 唯一地重建。
示例 4：

输入：org = [4,1,5,2,6,3], seqs = [[5,2,6,3],[4,1,5,2]]
输出：true
 

提示：

1 <= n <= 10^4
org 是 {1,2,...,n} 的一个排列
1 <= segs[i].length <= 10^5
seqs[i][j] 符合 32 位整数范围

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sequence-reconstruction
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.解题思路

力扣https://leetcode-cn.com/problems/sequence-reconstruction/solution/python-tuo-bu-pai-xu-yi-kan-jiu-dong-by-uwr7u/ 

3.代码实现

class Solution:
    def sequenceReconstruction(self, org: List[int], seqs: List[List[int]]) -> bool:
        if not seqs: 
            return False

        res = []
        nodes = set()
        for seq in seqs:
            nodes = nodes| set(seq)
        
        # 数量检查
        if len(org) != len(nodes) or set(org) != nodes:
            return False
        
        indegree = [0 for _ in range(len(nodes)+1)]
        # 注意这里和之前不同，之前初始化为set
        # org = [4,1,5,2,6,3], seqs = [[5,2,6,3],[4,1,5,2]]
        # 在这个例子中 5,2 共同出现2次，所以这里要初始化为list
        adj = [[] for _ in range(len(nodes)+1)]
        for seq in seqs:
            for i in range(len(seq)-1):
                indegree[seq[i+1]] += 1
                # 注意这里和之前不同，之前初始化为set
                adj[seq[i]].append(seq[i+1])
        que=[]
        for i in range(1, len(nodes)+1):
            if indegree[i] == 0:
                que.append(i)
        while que:
            # 唯一性：若同一层有不止一个则说明结果不唯一
            if len(que) > 1:
                return False
            t = que.pop(0)
            res.append(t)
            # 注意这里和之前不同，之前初始化为set
            # 这里adj中的每个元素也是list，当 5,2 共同出现2次时，会进行2词迭代，如果用set只会迭代一次
            for i in adj[t]:
                indegree[i] -= 1
                if indegree[i] == 0 and i!=0:
                    que.append(i)
        if res == org:
            return True
        else:
            return False