matlab评价模型和预测模型
先写在前面的话
这篇笔记写下来,感觉似乎在我所学范围内对着两种模型简单模式的使用好像并不广泛,也不见什么复杂的例子。复杂的模式也没有去讲……看看之后还有没有相关的内容吧,之后再补。
评价模型
加权平均
适用于每一项权重和评分都容易获得
对应的权重乘以对应的数值再求和。
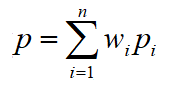
层次分析
适用于没有给出权重和分析,需要自己定义的情况
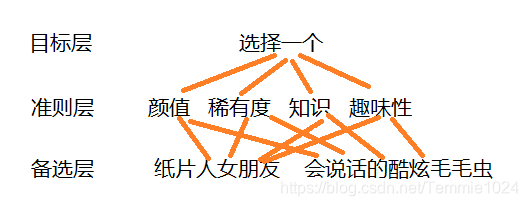
构造判断矩阵
准则
颜值C1 稀有度C2 知识C3 趣味性C4
两两比价:Ci相对于Cj的重要程度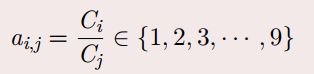
判断矩阵
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| C1 | 1/1 | 1/5 | 1/3 | 1/4 |
| C2 | 5/1 | 1/1 | 2/1 | 3/1 |
| C3 | 3/1 | 1/2 | 1/1 | 1/2 |
| C4 | 4/1 | 1/3 | 2/1 | 1/1 |

A12=1/5表示颜值和稀有度相比,稀有度更重要。
这里你也可以发现:
对角线元素为1/1(自己和自己比)
关于主对角线对称
要注意四个元素之间的大小关系,a>b>c>d,则矩阵中不应出现d>a这种矛盾的结果
一致性检验
一致性指标CI,一致性比例CR、平均随机一致性指标RI
n为判断矩阵的维数。λ为A矩阵的特征值。
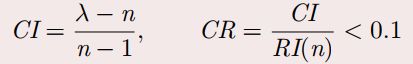
满足上面要求就为一致性较好。
RI不太清楚是怎么得来的,教程中直接给出的是这样的,好像就是一个固定的值

function [answer] = consistency_checking(A)
%一致性检验,一致性好与不好的判断
% 此处显示详细说明
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.14 1.45];
[m,n]=size(A)
[V,D]=eig(A);%计算特征向量V和特征值D:A*V=V*D
[lamda,i]=max(diag(D));
CI=(lamda-n)/(n-1);
CR=CI/RI(n)
if CR<0.1
answer='一致性较好';
else
answer='一致性不好';
end
end
层次单排序
function [answer] = consistency_checking(A)
%一致性检验,一致性好与不好的判断
% 此处显示详细说明
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.14 1.45];
[m,n]=size(A);
[V,D]=eig(A);%计算特征向量V和特征值D:A*V=V*D
[lamda,i]=max(diag(D));
CI=(lamda-n)/(n-1);
CR=CI/RI(n)
if CR<0.1
answer='一致性较好';
else
answer='一致性不好';
end
W=V(:,i);
w=W/sum(W)
end
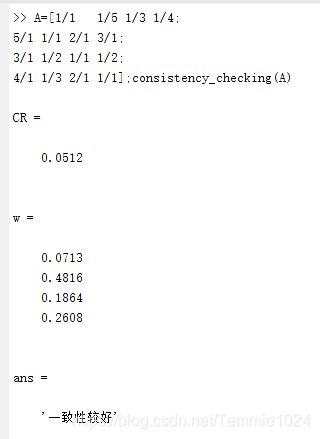
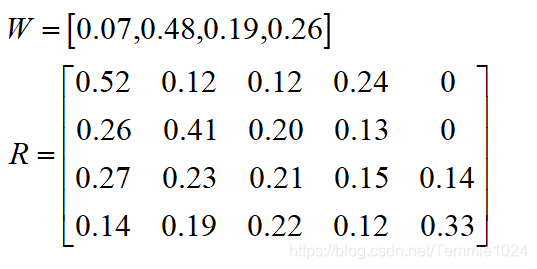
归一化:[0.0713 0.4816 0.1864 0.2608](值越大,说明权重越大,显然我不是颜控)
然后就可以打分计算了
结果显而易见

模糊综合评价:模糊数学
秃子悖论: 天下所有的人都是秃子
设头发的根数为 n, n = 1 显然为秃子。
若 n = k 为秃子,则 n = k + 1 亦为秃子。
模糊概念
从属于该概念到不属于该概念之间无明显分界线。
用隶属程度代替属或不属于,如某人属于秃子的程度为 0.8。
模糊综合评价
模糊综合评价要素
因素集: U={颜值 稀有度 知识 趣味性}
评语集: V={非常高 高 一般 低 非常低}
| 权重 | 纸片人 | 会说话的毛毛虫 | |
|---|---|---|---|
| 颜值 | 0.07 | [52 12 12 24 0] | [38 34 17 11 0] |
| 稀有度 | 0.48 | [26 41 20 13 0] | [32 22 23 23 0] |
| 知识 | 0.19 | [27 23 21 15 14] | [11 12 17 21 39] |
| 趣味性 | 0.26 | [14 19 22 12 33] | [26 27 12 21 14] |
预测模型
拟合
是最基本的预测方法。适用polyfit/fit进行拟合。
时间序列
时间序列: 将预测对象按照时间顺序排列而成的序列。
时序预测: 根据时序过去的变化规律,推测今后趋势。
时间序列的变化形式
长期趋势变动 Tt
季节变动 St
循环变动 Ct
不规则变动 Rt
模型
加法模型
乘法模型
混合模型
时间序列:移动平均法
感觉这种方法精度极差,是通过求取平均值作为后一个的结果。
一次移动平均法:

预测的标准误差

灰色预测
特点
1.模型使用的不是原始数据,而是生成数据。
2.不需要很多数据,一般只需 ≥ 4 个数据。
3.只适用于中短期的预测,只适合指数增长的预测。
GM(1,1) 预测模型
灰色模型一阶微分方程只含一个变量
需要满足以下条件才能使用
原始序列: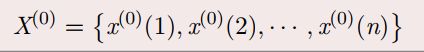
可行性检验条件:
满足就可以应用GM预测模型
如不满足可行性条件,这可作数据平移处理:
![]()
预测结束后在减去c
GM(1,1)预测模型步骤
一次累加生成序列

均值生成序列

灰微分方程
![]()
白化微分方程
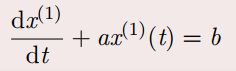
其中白化微分方程的a、b需要最小二乘法估计

白化微分方程求解
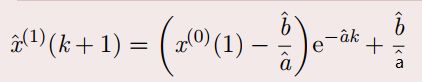
模型还原
![]()
检验
残差检验:(k) < 0:2
这个残差检验的公式不是很确定,在网上找到了两个版本,也无法考证哪个才是正确的,令一个版本没有分母。不过好在这个残差检验几乎不会使用,只需要在建立模型后观察图像走势就能大致确定效果好坏
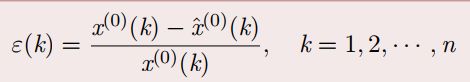
级比偏差值检验: ρ(k) < 0:2
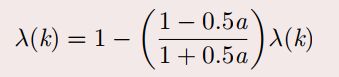
***************************************************************************************
这里发现一篇卖山楂啦prss大佬写的比较详细的文章,不过残差检验的公式和我上面写的有些不同,大家可以参考一下
***************************************************************************************
一个简单的灰度模型例子
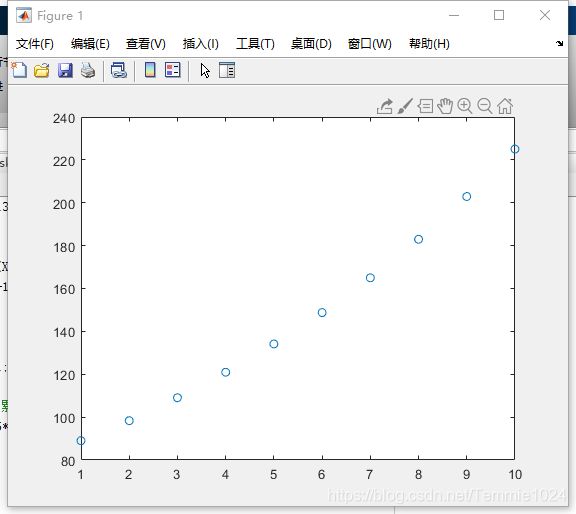
已知原始序列[89;99;109;120;135]预测未来走势
按照上面的讲解,先进行可行性检验,不可行就需要平移处理
X0=[89;99;109;120;135];
k1=length(X0);
k2=[2:k1]';
lamda=(X0(k2-1))./(X0(k2));%可行性检验
if lamda<exp(2/(k1+1)) & lamda>exp(-2/(k1+1))
answer='可行'
else
answer='不可行'
Y0(k1)=X0(k1)+1;%此处的1需要修改
end
然后按次序生成两个序列,产生B和Y两个矩阵,再用最小二乘法求解,这里我并没有写最后一个转置,以为无论怎么取,第一个都是a而第二个是b。
一定要好好看看矩阵运算,最开始用函数写的逆不好使,弄了好半天才想起右除这个方法才搞定!!
X1=cumsum(X0);%一次累加生成序列
Z1=0.5*X1(2:k1)+0.5*X1(1:k1-1);%均值生成序列
%求解a和b
Y=X0(2:k1)
B1=Z1
B2=ones(k1-1,1)
B=[-B1 B2]
xv=(B'*B)\B'*Y
a=xv(1)
b=xv(2)
下面代码中是白化微分方程
x_v=[0:k1+4];
X=(X0(1)-b/a).*exp(-a*x_v)+b/a
是不是和前面的那个式子等价?
这样,就可以用微分(diff)表示出2点及以后的值。而第一个点是已知的,直接带入即可。
XX=[X0(1) diff(X)]
全部的代码如下:
X0=[89;99;109;120;135];
k1=length(X0);
k2=[2:k1]';
lamda=(X0(k2-1))./(X0(k2));%可行性检验
if lamda<exp(2/(k1+1)) & lamda>exp(-2/(k1+1))
answer='可行'
else
answer='不可行'
Y0(k1)=X0(k1)+1;%此处的1需要修改
end
X1=cumsum(X0);%一次累加生成序列
Z1=0.5*X1(2:k1)+0.5*X1(1:k1-1);%均值生成序列
%求解a和b
Y=X0(2:k1);
B1=Z1;
B2=ones(k1-1,1);
B=[-B1 B2];
xv=(B'*B)\B'*Y;
a=xv(1);
b=xv(2);
x_v=[0:k1+4];
X=(X0(1)-b/a).*exp(-a*x_v)+b/a;
XX=[X0(1) diff(X)];
plot(XX,'o')