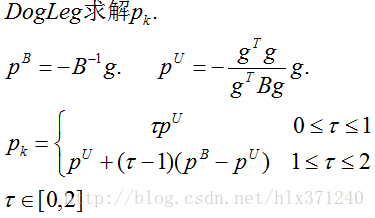狗腿算法整理
f(xk+P)泰勒展开有
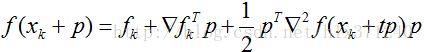
(1)
优化算法的目的是:min f(xk+p),pk为下降方向。 f(xk+p)
可以用泰勒公式展开为

(2)
其中
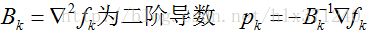


dogleg的程序中包含了如下三个小函数:
f_x_result函数用来求两点的差值:
q_x_result函数用来求近似情况下两点的差值:
转自: 点击打开链接
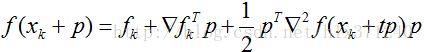
(1)
优化算法的目的是:min f(xk+p),pk为下降方向。 f(xk+p)
可以用泰勒公式展开为

(2)
其中
tao 的求法
- if p_u'*p_u > pars.trustRegionBound*pars.trustRegionBound;
- tao = pars.trustRegionBound / sqrt((p_u'*p_u));
- else if p_b'*p_b > pars.trustRegionBound*pars.trustRegionBound
- tao = sqrt((pars.trustRegionBound*pars.trustRegionBound - p_u'*p_u) / ((p_b-p_u)'*(p_b-p_u))) + 1;
- end
- end


主程序(demo_dogleg):
%programed by Lu Qi,UCAS
%my email:[email protected]
global syms x y
pars.f_x_y=100*(y - x^2).^2 + (1 - x)^2;
pars.dfdx=diff(pars.f_x_y,x,1);
pars.dfdy=diff(pars.f_x_y,y,1);
pars.df2dxdy=diff(pars.dfdx,y,1);
pars.df2dx2=diff(pars.dfdx,x,1);
pars.df2dy2=diff(pars.dfdy,y,1);
pars.trustRegionBound=10; %信赖域
pars.tao=2; %tao的初始化
pars.x0=[-9 -9]'; %初始点的坐标
[x_final,num_iter]=dogleg(pars);
fprintf('x_final= \n');
[m, n] = size(x_final);
for i = 1 : m
for j = 1 : n
fprintf('%8.4f', x_final(i, j));
end
fprintf('\n');
end
fprintf('num_iter=%d',num_iter);
下面是实现dogleg算法的程序(dogleg):
function [x_final,i]=dogleg(pars)
global syms x y
%programed by Lu_Qi
temp=pars.x0;
temp_x=temp(1);
temp_y=temp(2);
calculate;
fan_g_x=sum(abs(pars.g_x));
tao=pars.tao;
i=1;
while(1)
if(fan_g_x<=0.00001)
break
end
fprintf('iter=%d\n',i);
d_u=pars.g_x'*pars.g_x/(pars.g_x'*pars.b_x*pars.g_x);
d_u=-d_u*pars.g_x;
d_b=inv(pars.b_x);
d_b=-d_b*pars.g_x;
if d_u'*d_u > pars.trustRegionBound*pars.trustRegionBound;
tao = pars.trustRegionBound / sqrt((d_u'*d_u));
else if d_b'*d_b > pars.trustRegionBound*pars.trustRegionBound
tao = sqrt((pars.trustRegionBound*pars.trustRegionBound - d_u'*d_u) / ((d_b-d_u)'*(d_b-d_u))) + 1;
end
end
if tao <=1 && tao >= 0
d_tao = tao * d_u;
else if tao <=2 && tao >= 1
d_tao = d_u + (tao - 1) * (d_b - d_u);
end
end
p=((f_x_result(pars,temp_x,temp_y,d_tao))/(q_x_result(pars,d_tao)));
if p > 0.75 && abs(d_tao'*d_tao)==pars.trustRegionBound
pars.trustRegionBound = min(2 * pars.trustRegionBound, 3);
else if p < 0.25
pars.trustRegionBound = sqrt(abs(d_tao'*d_tao)) * 0.25;
end
end
if p > 0
temp = temp + d_tao;
end
temp_x=temp(1);
temp_y=temp(2);
calculate;
fan_g_x=sum(abs(pars.g_x));
i=i+1;
end
x_final=temp; dogleg的程序中包含了如下三个小函数:
calculate函数,用来求在某一坐标下的g(x)和b(x)的值:
%calculate g_x b_x
old={x,y};
new={temp_x ,temp_y};
pars.g_x=[subs(pars.dfdx,old, new);subs(pars.dfdy,old, new)];
pars.b_x=[subs(pars.df2dx2,old, new) subs(pars.df2dxdy,old, new);
subs(pars.df2dxdy,old, new) subs(pars.df2dy2,old, new) f_x_result函数用来求两点的差值:
function result=f_x_result(pars,temp_x,temp_y,d)
%
global syms x y
old={x,y};
new={temp_x ,temp_y};
result=subs(pars.f_x_y,old, new);
new={temp_x+d(1),temp_y+d(2)};
result=result-subs(pars.f_x_y,old, new); q_x_result函数用来求近似情况下两点的差值:
function result=q_x_result(pars,d_tao)
%
result=-(d_tao'*pars.g_x+0.5*d_tao'*pars.b_x*d_tao); 转自: 点击打开链接
点击打开链接