几种重要的排序算法——插入排序

插入排序

1.插入排序

插入排序分为直接插入排序、折半插入排序、希尔排序（shell sort），后两种是在直接插入排序的改进上而来。

1.直接插入排序

排序思路：假设待排序的元素存放在数组$A[1..n]$中，在排序过程的某一时刻，A被划分为两个子区间$A[1..mid]$和$A[mid+1..n]$，其中前一个子区间为排好序的有序区，而后一个子区间为未排序的子区间，暂称作无序区。该排序算法顾名思义，取出无序区的第一个元素$A[mid+1]$插入到有序区$A[1..mid]$中适当的位置，$A[1..mid+1]$变成新的有序区（假设按照升序排序）。动画演示如下：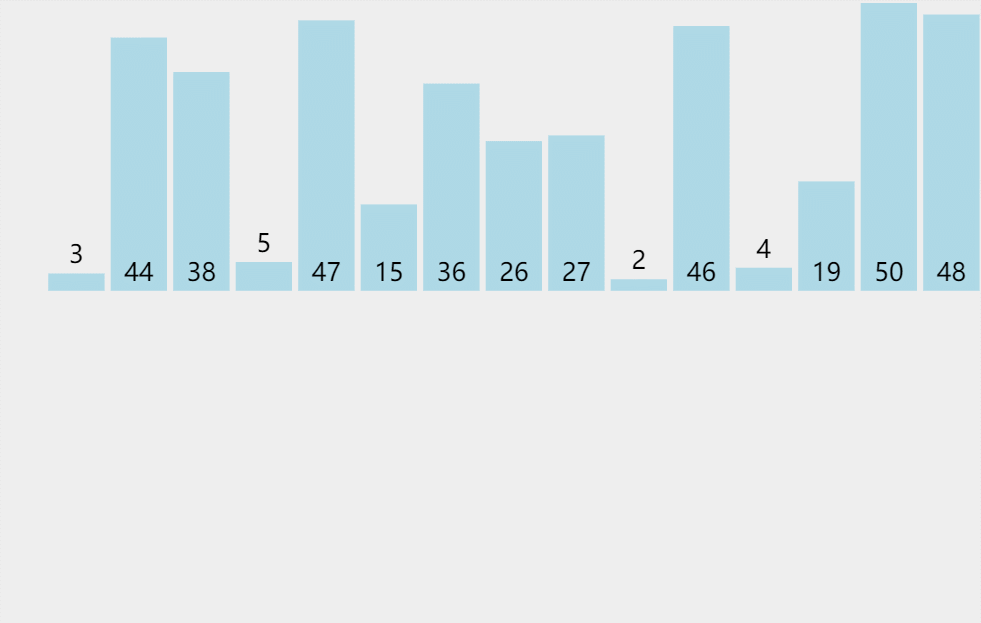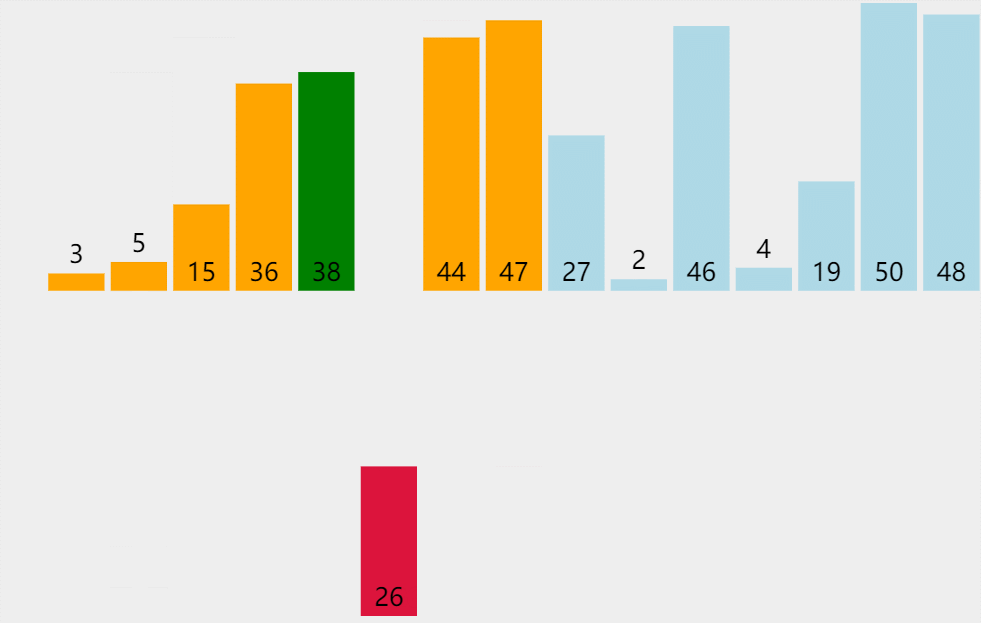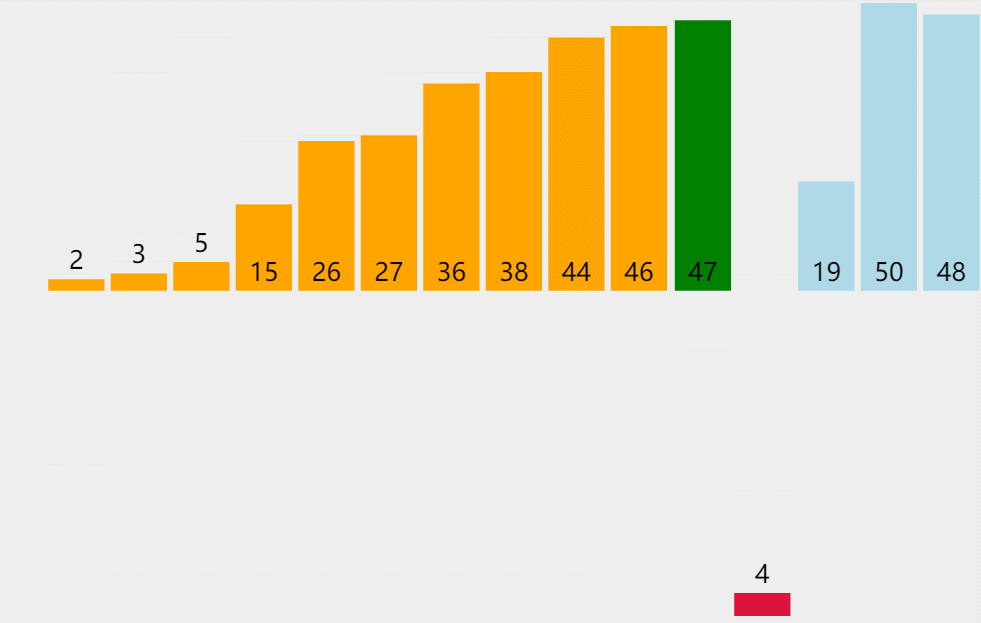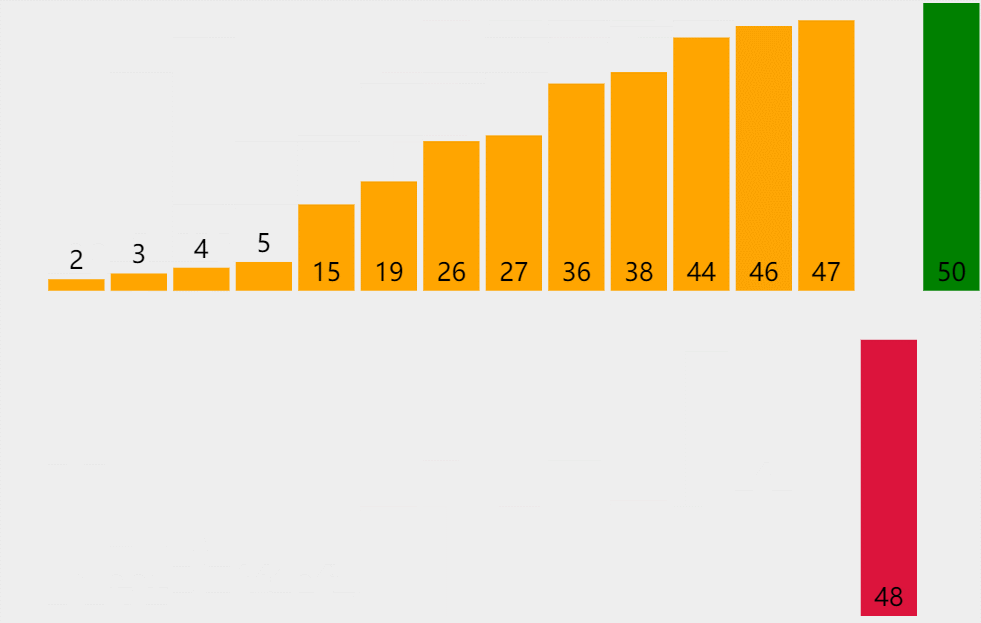
对于第i趟排序，要将无序区的第一个元素$A[mid+1]$（设$A[mid+1]的值为a$）插入到有序区的适当位置，此时便将$a$不断的与有序区的元素进行比较（即为动画中红色条形与绿色条形的部分），当找到第一个比$a$小的元素时（假设是$A[m](1\le m<mid+1)$），在该元素的后面将$a$插入,当a是有序区中最小的元素时，将a放在有序区的第一个位置，此时数组中下标$m+1$到$mid$的所有元素均要往后移动一格，就像是腾出一个位置来让给$a$，然后把$a$放到数组中$m$的位置。

c/c++代码描述:

void InsertSort(int A[], int n)
{
	int i, j;
	for (int i = 2; i <= n; i++)	// 依次将A[2]~A[n]插入到前面已经有序区
	{
		if (A[i] < A[i - 1])		// A[i]小于其前面的元素，将A[i]放入有序区
		{
			A[0] = A[i];			// A[0]不存放元素，专用于来存放当前需要插入的值
			for (j = i - 1; A[j] > A[0]; j--)	// 从后往前寻找插入位置，直至找到第一个比A[i]小的元素时停止
				A[j + 1] = A[j];	// 向后挪一个位置，腾出地方让给A[i]
		}
		A[j + 1] = A[0];			// A[i]归位，放到有序区合适的位置
	}
}

python代码描述:

def insert_sort(a):
    length = len(a)
    for i in range(1,length):
        waitting_insert_ele = a[i]
        j = i - 1
        while j > -1 and a[j] > waitting_insert_ele: # 与前面有序区进行比较，如果比前面有序区第一个大，则停止，将该元素插入此位置
            a[j + 1] = a[j]             # 后移操作，给待插入元素“腾位置”
            j -= 1
        a[j+1] = waitting_insert_ele    # 当不比前面的数值小时，便在当前位置“赖着不走”
    print(a)
a = [3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]
insert_sort(a)

运行结果如下：

算法分析:  
空间复杂度：因为直接插入排序并没有开第二个数组，它仅仅只是就着他自己的原来的数组进行排序，利用的存储空间是常数个空间，因而其空间复杂度为$O(1)$，即原地工作。 
时间复杂度：在排序过程中，向有序区逐个的插入元素进行了$n-1$趟，每趟都分为两步： 

• 和前一元素进行比较
• 将前一元素进行往后挪

其中比较的次数与待排序数组的初始状态有关，在最优情况下，表中元素已有序，此时每遍历一次，都不用移动元素，且只需比较一次，时间复杂度为$O(n)$。在最坏情况下，数组中元素与要排序顺序相反（在本博客中以初始时降序排列为反序），总的比较次数达到最大均为$O(n^2)$。平均情况下总的比较次数和移动次数约为$\frac{n^2}{4}$，所以时间复杂度为$O(n^2)$。 
稳定性：每次插入元素时，总是从后向前比较再移动，所以相同元素的相对位置不会发生变化，直接插入排序是一个稳定的排序算法。 
适用性：直接插入排序适用于顺序存储和链式存储的线性表。

2.折半插入排序

排序思路: 思路同直接插入排序一致，但在进行元素比较时采用的是折半查找，在查找待插入位置时时间复杂度为$O(nlo{g}_{2}n)$（折半查找的时间复杂度）。

c/c++代码描述:

void InsertSort(int A[], int n)
{
	int i, j, low, high, mid;
	for (int i = 2; i <= n; i++) // 依次将A[2]~A[n]插入到前面已经有序区
	{
		A[0] = A[i]; // A[0]不存放元素，专用于来存放当前需要插入的值
		low = 1;
		high = i - 1;
		while (low < high)
		{
			mid = (low + high) / 2; //取中间节点
			if (A[mid] > A[0])
				high = mid - 1; // 插入位置应在左半子表，即有序区的前半部分
			else
				low = mid + 1; // 插入位置应在右半子表，即有序区的后半部分
		}
		for (j = i - 1; j > high + 1; j--) // 从后往前寻找插入位置，直至找到第一个比A[i]小的元素时停止
			A[j + 1] = A[j];			   // 向后挪一个位置，腾出地方让给A[i]
		A[high + 1] = A[0];				   // A[i]归位，放到合适的地方
	}
}

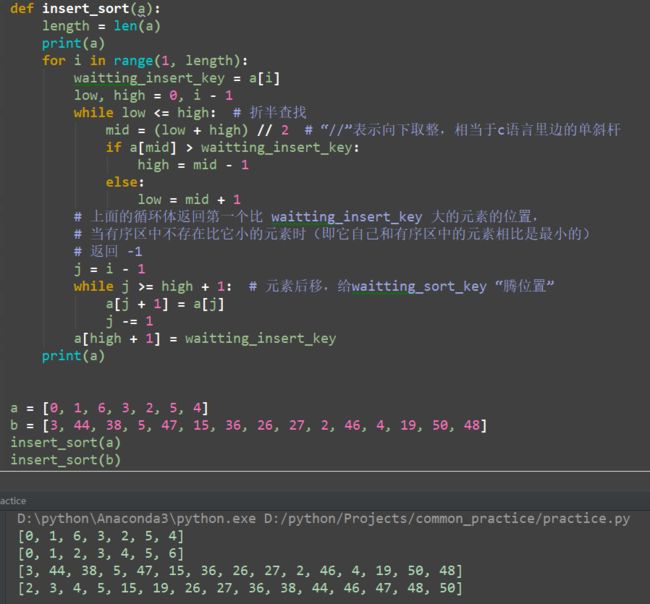
python代码描述:

def insert_sort(a):
    length = len(a)
    print(a)
    for i in range(1, length):
        waitting_insert_key = a[i]
        low, high = 0, i -1
        while low <= high:  # 折半查找
            mid = (low + high) // 2     # “//”表示向下取整，相当于c语言里边的单斜杆
            if a[mid] > waitting_insert_key:
                high = mid - 1
            else:
                low = mid + 1
        # 上面的循环体返回第一个比 waitting_insert_key 大的元素的位置，
        # 当有序区中不存在比它小的元素时（即它自己和有序区中的元素相比是最小的）
        # 返回 -1
        j = i - 1
        while j >= high + 1:    # 元素后移，给waitting_sort_key “腾位置”
            a[j + 1] = a[j]
            j -= 1
        a[high + 1] = waitting_insert_key
    print(a)
a = [0,1,6,3,2,5,4]
b = [3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]
insert_sort(a)
insert_sort(b)

运行结果如下：

算法分析:  折半插入排序仅仅只是减少了比较的时间而已，而对于腾出空间的挪动操作并未有改变，挪动次数取决于元素在存储结构中的初始位置，若初始表中数据整体有序的较多，则移动次数较少，因此折半插入排序的时间复杂度仍然是$O(n^2)$。折半插入排序是一种稳定的排序算法。

3.希尔排序(shell sort)

排序思路: 先将待排序的元素分组，从初始表中每相隔距离d取一个元素，形如$L[i,i+d,i+2d,i+3d,...,i+kd]$，首次可将n个元素划分成$d$个组（即从第1个元素到第d个元素直接的所有元素是每组的第一个元素，“头儿”），每次分别对这些组进行直接插入排序，当整个表中的元素已基本有序时，再对全体记录进行一次直接插入排序。希尔排序每趟并不产生有序区，在最后一趟排序结束前，所有元素并不一定归位了，但是在希尔排序每趟完成后数据越来越接近有序。动画效果如下（演示动画仅进行了一次分组，第二趟排序便直接对整个序列进行排序了）：
动画中演示的是先将分组中值较大的调整至后面，再将值较小的调整至前。

c/c++代码描述:

void shellSort(int A[], int n)
{
	int d, i, j;
	for (d = n / 2; d >= 1; d / 2) //每次分组的间隔长度，步长变化
		for (i = d + 1; i <= n; i++)
			if (A[i] < A[i - d]) //需将A[i]插入有序区
			{
				A[0] = A[i];
				for (j = i - d; j > 0 && A[j] > A[0]; j -= d)
					A[j + d] = A[j]; // 给小组中后面值较小的元素挪位置，让较小的元素尽量往前边靠
				A[j + d] = A[0];	 // 最终归位
			}
}

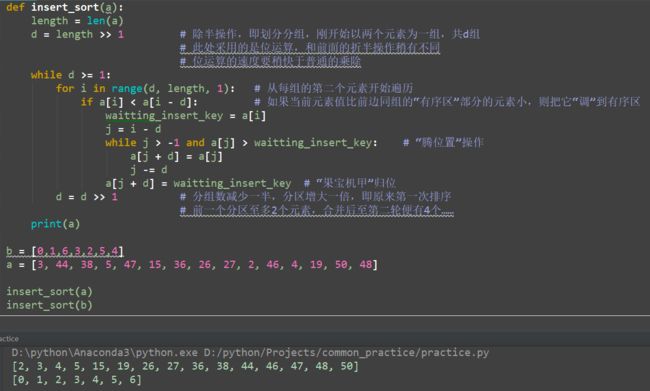
python代码描述:

def insert_sort(a):
    length = len(a)
    d = length >> 1         # 除半操作，即划分分组，刚开始以两个元素为一组，共d组
                            # 此处采用的是位运算，和前面的折半操作稍有不同
                            # 位运算的速度要稍快于普通的乘除
    while d >= 1:
        for i in range(d, length, 1):   # 从每组的第二个元素开始遍历
            if a[i] < a[i - d]:         # 如果当前元素值比前边同组的“有序区”部分的元素小，则把它“调”到有序区
                waitting_insert_key = a[i]
                j = i - d
                while j > -1 and a[j] > waitting_insert_key:    # “腾位置”操作
                    a[j + d] = a[j]
                    j -= d
                a[j + d] = waitting_insert_key  # “果宝机甲”归位
        d = d >> 1          # 分组数减少一半，分区增大一倍，即原来第一次排序
                            # 前一个分区至多2个元素，合并后至第二轮便有4个……
    print(a)

b = [0,1,6,3,2,5,4]
a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

insert_sort(a)
insert_sort(b)

运行结果如下：

算法分析: 
空间复杂度：因为希尔排序并没有使用第二个数组，它仅仅只是就着他自己的原来的数组进行排序，使用存储空间为常数个空间，因而其空间复杂度为$O(1)$。 
时间复杂度：由于希尔排序的时间复杂度依赖于增量序列的函数，这涉及数学上未解决的难题，所以其时间复杂度分析比较困难。当n在某个特定范围时，希尔排序的时间复杂度约为$O(n^{1.3})$。在最坏情况下希尔排序的时间复杂度为$O(n^2)$。 
稳定性：希尔排序是一种不稳定的排序算法。
适用性：希尔排序仅适用于线性表为顺序存储的情况。

 
 
后记： 文章中的python代码的运行示例的pycharm风格不同是因为文章是断断续续写的，前两张的运行截图是借同学的电脑运行的截图，后一张是自己吃完晚饭在自己电脑上截的图。平常要忙着考研复习，只有中午、晚上吃完饭回寝室才有时间写一下，文章连着写了好几天才写完。后面也会挤时间陆续把其他的几个基础算法补齐的。欢迎各位大佬指正文中不足的部分，弟弟以后定加改正！