前端算法相关

目录

时间复杂度

1、五大算法

2、基础排序算法

2.选择排序

3.插入排序

3、高级排序算法

1.快速排序

 2.希尔排序

4、递归运用(斐波那契数列)： 爬楼梯问题

5、数据树

6、天平找次品

---

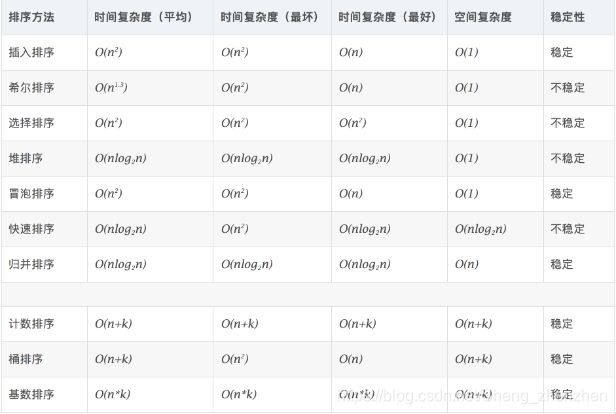
时间复杂度

口诀：插冒归基稳定，快选堆希不稳定

稳定性： 同大小情况下是否可能会被交换位置, 虚拟dom的diff，不稳定性会导致重新渲染；

1、五大算法

1.贪心算法：局部最优解法

2.分治算法：分成多个小模块，与原问题性质相同

3.动态规划：每个状态都是过去历史的一个总结

4.回溯法：发现原先选择不优时，退回重新选择

5.分支限界法

2、基础排序算法

 1.冒泡排序

它的名字由来于一副图——鱼吐泡泡，泡泡越往上越大。

思路：第一次循环，开始比较当前元素与下一个元素的大小，如果比下一个元素小或者相等，则不需要交换两个元素的值；若比下一个元素大的话，则交换两个元素的值。然后，遍历整个数组，第一次遍历完之后，相同操作遍历第二遍。

let arr = [5,7,1,6,2,3,9,4,8];
function bubbleSort(arr){
    for(let i = 0; i < arr.length - 1; i++){
        for(let j = 0; j < arr.length - i - 1; j++){
            if(arr[j] > arr[j + 1]){ 
                //交换位置
                [arr[j],arr[j+1]]=[arr[j+1],arr[j]]
            }
        }
    }  
    return arr;
}
 
bubbleSort(arr);
console.log(arr); //[1,2,3,4,5,6,7,8,9]

2.选择排序

遍历自身以后的元素，最小的元素跟自己调换位置

function selectSort(arr) {
    var len = arr.length;
    for(let i = 0 ;i < len - 1; i++) {
        for(let j = i + 1; j

3.插入排序

即将元素插入到已排序好的数组中

function insertSort(arr) {
    for(let i = 1; i < arr.length; i++) {  //外循环从1开始，默认arr[0]是有序段
        for(let j = i; j > 0; j--) {  //j = i,将arr[j]依次插入有序段中
            if(arr[j] < arr[j-1]) {
                [arr[j],arr[j-1]] = [arr[j-1],arr[j]];
            } else {
                break;
            }
        }
    }
    return arr;
}

3、高级排序算法

1.快速排序

基本原理：快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

1.选择数组中第一个元素作为基准数；

2.遍历数组中其他元素，与基准数比较，小于基准数的放入左边的数组，其余放入右边数组；

3.递归调用函数，遍历左边和右边数组，直至参数个数为1，最后按顺序合并数组。

function quickSort(arr){
    if(arr.length<=1){
        return arr;
    }
    let left=[],right=[];
    let current=arr.splice(0,1);
    for(let i=0;i

 2.希尔排序

不定步数的插入排序

4、递归运用(斐波那契数列)： 爬楼梯问题

问题描述：一个人爬楼梯，只可以一步走一层或一步走两层，共多少种走法？
输入：楼梯总层数
输出：有几种走法
解：
这个问题，是一个递归问题。
1.楼梯总层数为1，有一种走法，一步走一层。
2.楼梯总层数为2，有两种走法：
1）一步走一层，走两步
2）一步走两层，走一步
3.楼梯总层数为n的走法有多少种呢？
走到n层只有两种可能：
1）在第n-1层往上走1步（一步一层）到第n层
2）在第n-2层往上走1步（一步两层）到第n层
所以：
楼梯总层数为n的走法=楼梯总层数为n-1的走法+楼梯总层数为n-2的走法
类似于斐波那契数列，只不过第0层是0种走法。
注：0层0种，1层1种，2层2种，3层=2层+1层，4层=3层+2层，…

function cStairs(n) {
    if(n === 1 || n === 2) {
        return n;
    } else {
        return cStairs(n-1) + cStairs(n-2)
    }
}

5、数据树

1.二叉树：最多只有两个子节点

• 完全二叉树
• 满二叉树
  • 深度为 h, 有 n 个节点，且满足 n = 2^h - 1

2.二叉查找树：是一种特殊的二叉树，能有效地提高查找效率

• 小值在左，大值在右
• 节点 n 的所有左子树值小于 n，所有右子树值大于 n

6、天平找次品

有n个硬币，其中1个为假币，假币重量较轻，你有一把天平，请问，至少需要称多少次能保证一定找到假币?

三等分算法:
将硬币分成3组，随便取其中两组天平称量
平衡，假币在未上称的一组，取其回到 1 继续循环
不平衡，假币在天平上较轻的一组， 取其回到 1 继续循环

7、贪心算法

给定一个非负整数数组，你最初位于数组的第一个位置，数组中的每个元素代表你在该位置可以跳跃的最大长度，判断你是否能够到达最后一个位置。

输入：[2，3，1，1，4]

输出：true

const canJump = function (nums){
    let maxJump = nums.length-1;
    for(let i=nums.length-2;i>=0;i--){
        if(i+nums[i]>=maxJump){
            maxJump = i;
        }
    }
    return maxJump===0;
}