大数据HCIE成神之路之数学（4）——最优化实验

1.1 最小二乘法实现

1.1.1 算法介绍

最小二乘法（Least Square Method），做为分类回归算法的基础，有着悠久的历史。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的参数，并使得预测的数据与实际数据之间误差的平方和为最小。

通俗地解释：最小二乘法是一种数学方法，它可以帮助我们找到一条直线，使得这条直线与一些散点数据的距离之和最小。这就像是在一堆点中找到一条最合适的线，使得这条线与所有点的距离之和最小。

1.1.2 代码实现

代码输入：

import numpy as np  
import scipy as sp  
import pylab as pl  
from scipy.optimize import leastsq  # 引入最小二乘函数  

n = 9  # 多项式次数  

# 定义目标函数：  
def real_func(x):  
	 #目标函数：sin(2*pi*x)
    return np.sin(2 * np.pi * x)  

# 定义多项式函数，用多项式去拟合数据:  
def fit_func(p, x):  
    f = np.poly1d(p)  # 构造一个多项式
    return f(x)  

# 定义残差函数，残差函数值为多项式拟合结果与真实值的差值：  
def residuals_func(p, y, x):  
    ret = fit_func(p, x) - y  # 计算残差
    return ret  

x = np.linspace(0, 1, 9)  # 随机选择9个点作为x  
x_points = np.linspace(0, 1, 1000)  # 画图时需要的连续点  
y0 = real_func(x)  # 目标函数  
y1 = [np.random.normal(0, 0.1) + y for y in y0]  # 在目标函数上添加符合正态分布噪声后的函数  
p_init = np.random.randn(n)  # 随机初始化多项式参数  

# 调用scipy.optimize中的leastsq函数，通过最小化误差的平方和来寻找最佳的匹配函数
#func是一个残差函数，x0是计算的初始参数值，把残差函数中除了初始化以外的参数打包到args中
plsq = leastsq(func=residuals_func, x0=p_init, args=(y1, x))  

print('Fitting Parameters: ', plsq[0])  # 输出拟合参数  

# 绘制图像
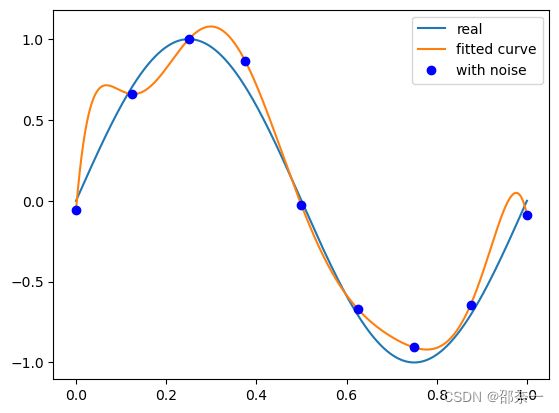
pl.plot(x_points, real_func(x_points), label='real')  # 绘制真实函数
pl.plot(x_points, fit_func(plsq[0], x_points), label='fitted curve')  # 绘制拟合函数
pl.plot(x, y1, 'bo', label='with noise')  # 绘制带有噪声的数据点
pl.legend()  # 显示图例
pl.show()  # 显示图像

结果输出：

Fitting Parameters:   [-4.43705803e+03  1.82907420e+04 -3.09056669e+04  2.74461105e+04
 -1.36135812e+04  3.70056478e+03 -5.14095149e+02  3.29570051e+01
 -5.85714263e-02]

可视化图像：

解释1：

# 定义多项式函数，用多项式去拟合数据:  
def fit_func(p, x):  
    f = np.poly1d(p)  # 构造一个多项式
    return f(x)  

这个函数 fit_func 的作用是计算多项式的值。在这个函数中，np.poly1d(p) 用于构造一个多项式。p 是一个一维数组，代表多项式的系数，从高次项到低次项。例如，如果 p=[1,2,3]，那么 np.poly1d(p) 就会构造一个多项式 f(x) = 1*x^2 + 2*x + 3。然后，f(x) 会计算这个多项式在 x 处的值。

举个例子，如果我们有一个二次多项式 f(x) = 2*x^2 + 3*x + 4，我们可以用 p=[2,3,4] 来表示。如果我们想要计算 x=5 时这个多项式的值，我们可以调用 fit_func([2,3,4], 5)，这将返回 2*5^2 + 3*5 + 4 = 69。所以，fit_func([2,3,4], 5) 的返回值就是 69，这就是这个函数的作用。

解释2：

plsq = leastsq(func=residuals_func, x0=p_init, args=(y1, x)) 

leastsq 是 SciPy 库中的一个函数，用于执行最小二乘拟合。最小二乘拟合是一种数学优化技术，它通过最小化预测值和实际值之间的平方差来找到数据的最佳函数匹配。

在这段代码中，leastsq 函数有三个参数：

• func 是计算误差的函数，这里使用的是 residuals_func，它计算的是拟合函数和实际数据之间的差值。
• x0 是待优化的参数的初始猜测值，这里使用的是 p_init，它是一个随机初始化的多项式参数。代码上面有 p_init = np.random.randn(n) ，n=9，所以p_init将会有9个数的数组。 p_init 其实就是 np.poly1d(p) 函数的参数 p 。
• args 是传递给 func 的额外参数，在这里是 (y1, x)，其中 y1 是带有噪声的目标函数值，x 是自变量的值。

leastsq 函数会返回两个值，但在这里我们只关心第一个值，即最优参数值，所以我们用 plsq 来接收这个值。

举个例子，假设我们有一组数据 x=[1,2,3,4,5]，y=[2.2, 2.8, 3.6, 4.5, 5.1]，我们想要找到一个最佳的线性函数 y=ax+b 来拟合这组数据。我们可以先随机初始化 a 和 b 的值，然后调用 leastsq 函数来找到最佳的 a 和 b 值。这就是这段代码的作用，其实上面的args里的y1相当于这个例子里的y，args里的x相当于这个例子的x。

1.2 梯度下降法实现

1.2.1 算法介绍

梯度下降法（gradient descent），又名最速下降法，是求解无约束最优化问题最常用的方法，它是一种迭代方法，每一步主要的操作是求解目标函数的梯度向量，将当前位置的负梯度方向作为搜索方向（因为在该方向上目标函数下降最快，这也是最速下降法名称的由来）。

梯度下降法特点：越接近目标值，步长越小，下降速度越慢。

1.2.2 代码实现

代码输入：

训练集 (x,y) 共5个样本,每个样本点有3个分量 (x0,x1,x2)

# 定义数据集
x = [(1, 0., 3), (1, 1., 3), (1, 2., 3), (1, 3., 2), (1, 4., 4)]  
# 输入数据
y = [95.364, 97.217205, 75.195834, 60.105519, 49.342380]  # 对应的真实值  
epsilon = 0.0001  # 迭代阀值，当两次迭代损失函数之差小于该阀值时停止迭代  
alpha = 0.01  # 学习率
diff = [0, 0]  # 初始化残差
max_itor = 1000  # 最大迭代次数
error1 = 0  # 初始化误差，表示后一次误差，需减去前一次误差看是否在迭代阈值之内，之内则停止迭代
error0 = 0  # 初始化误差，表示前一次误差
cnt = 0  # 初始化迭代计数
m = len(x)  # 数据集大小，m=5

# 初始化参数  
theta0 = 0  
theta1 = 0  
theta2 = 0  

# 开始迭代
while True:  
    cnt += 1  # 迭代计数加1

    # 参数迭代计算（m=5）
    for i in range(m):  
        # 拟合函数为 y = theta0 * x[0] + theta1 * x[1] +theta2 * x[2]  
        # 计算残差，即拟合函数值-真实值  
        diff[0] = (theta0 * x[i][0]