树结构的知识架构+二叉树的知识架构(含顺序与链式存储C语言完整代码实现)+树和森林与二叉树的转换
前言:
树的概念比较多,适合查漏补缺,重新温习一下。文章末尾附带二叉树实现的完整代码:
附录1:二叉树的顺序结构实现
附录2:二叉树的链式结构实现
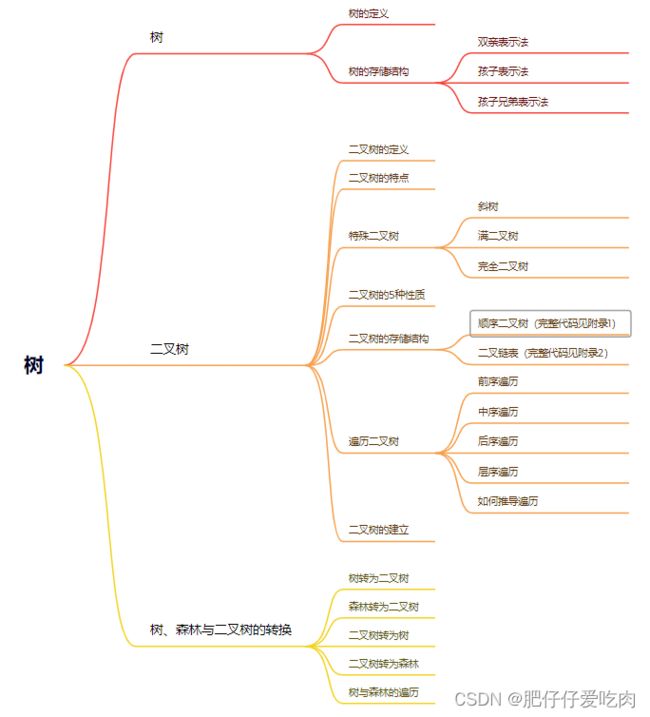
框架图:
目录
前言:
一、树结构的基础
1.树结构的定义
1.1结点的分类:
1.2结点间的关系 :
1.3结点的层次:
1.4其他
2.树的存储结构
2.1双亲表示法:
2.2孩子表示法:
2.3孩子兄弟表示法:
二、二叉树
1.二叉树的定义
2.二叉树的特点
3.特殊二叉树
3.1斜树:
4.2满二叉树:
4.3完全二叉树:
4.二叉树的性质
5.二叉树的存储结构
5.1顺序存储
5.2 二叉链表
6.二叉树的遍历
6.1前序遍历:
6.2中序遍历:
6.3后序遍历:
6.4层序遍历:
6.5推导遍历:
7.二叉树的建立
三、树、深林、二叉树的转换
1. 树转换为二叉树
2.森林转换为二叉树
3 .二叉树转换为树
4. 二叉树转换为森林
5.树与森林的遍历
参考:
一、树结构的基础
1.树结构的定义
树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一棵非空树中:
(1)有且仅有一个特定的称为根(Root)的结点;
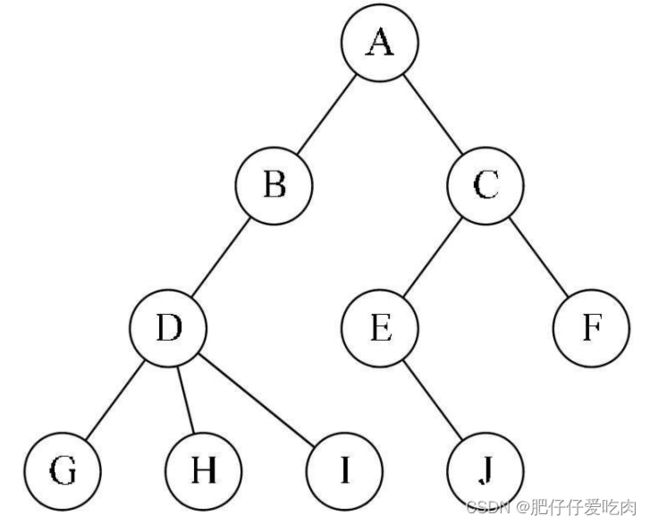
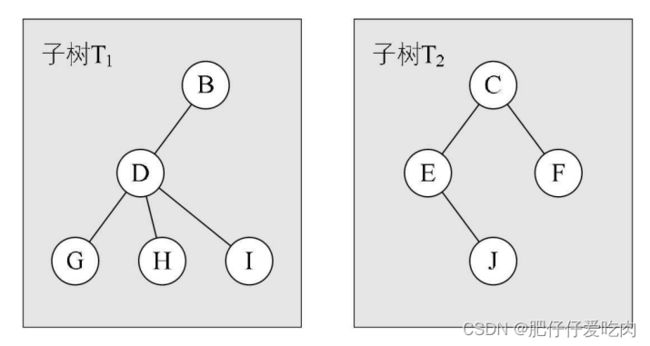
(2)当n>1时,其余结点可分为 m(m>0)个互不相交的有限集T1、T2、……、Tm,其中每一个集合本身又是一棵树,并且称为根的子树。
其中子树T1和子树T2就是根结点A的子树。当然,D、G、H、I组成的树又是B为根结点的子树,E、J组成的树是以C为根结点的子树。
此外树结构也是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
(1) 树的根结点没有前驱,除根结点外的所有结点有且只有一个前驱。
(2) 树中所有结点可以有零个或多个后继。
因此n个结点的树中有n-1条边。
下图两个结构就不符合树的定义,因为它们都有相交的子树。
1.1结点的分类:
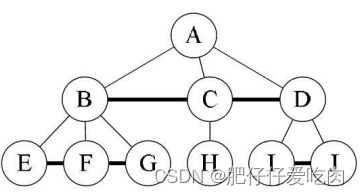
树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的度(De-gree)。度为0的结点称为叶结点(Leaf)或终端结点;度不为0的结点称为非终端结点或分支结点。除根结点之外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。如下图所示,因为这棵树结点的度的最大值是结点D的度,为 3,所以树的度也为3。
1.2结点间的关系 :
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲 (Parent)。嗯,为什么不是父或母,叫双亲呢?呵呵,对于结点来说其父母同体, 唯一的一个,所以只能把它称为双亲了。同一个双亲的孩子之间互称兄弟 (Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。所以对于H来说, D、B、A都是它的祖先。反之,以某结点为根的子树中的任一结点都称为该结点的子 孙。B的子孙有D、G、H、I,如下图所示。
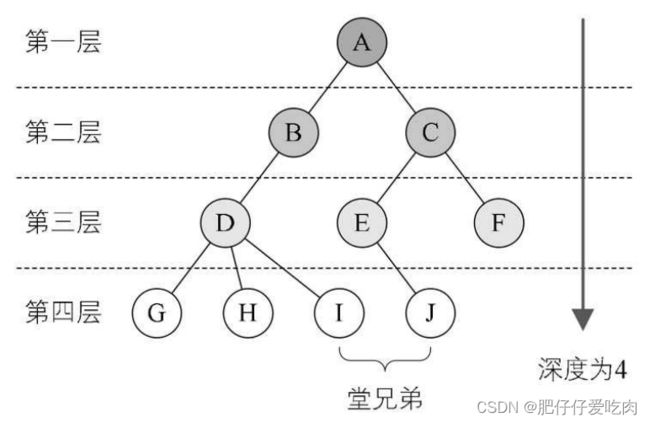
1.3结点的层次:
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。若某结点在第l层,则其子树就在第l+1层。其双亲在同一层的结点互为堂兄弟。显然下图中的 D、E、F是堂兄弟,而G、H、I与J也是堂兄弟。树中结点的最大层次称为树的深度 (Depth)或高度,当前树的深度为4。
1.4其他
如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
森林(Forest)是m(m≥0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。两棵子树其实就可以理解为森林。 对比线性表与树的结构,它们有很大的不同,如下图所示。
2.树的存储结构
这里介绍三种不同的表示法:双亲表示法、孩子表示法、孩子兄弟表示法。
2.1双亲表示法:
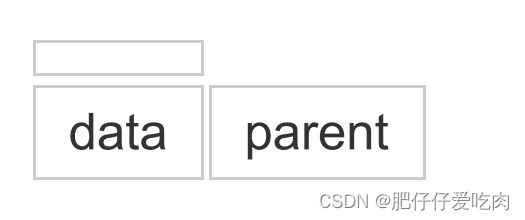
我们假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点在数组中的位置。也就是说,每个结点除了知道自己是谁以外,还知道它的双亲在哪里。它的结点结构为下图所示。
其中data是数据域,存储结点的数据信息。而parent是指针域,存储该结点的双亲在数组中的下标。
结点结构定义代码如下:
/* 树的双亲表示法结点结构定义 */
#define MAX_TREE_SIZE 100
/* 树结点的数据类型,目前暂定为整型 */
typedef int TElemType;
/* 结点结构 */
typedef struct PTNode
{
/* 结点数据 */
TElemType data;
/* 双亲位置 */
int parent;
} PTNode;
/* 树结构 */
typedef struct
{
/* 结点数组 */
PTNode nodes[MAX_TREE_SIZE];
/* 根的位置和结点数 */
int r, n;
} PTree;
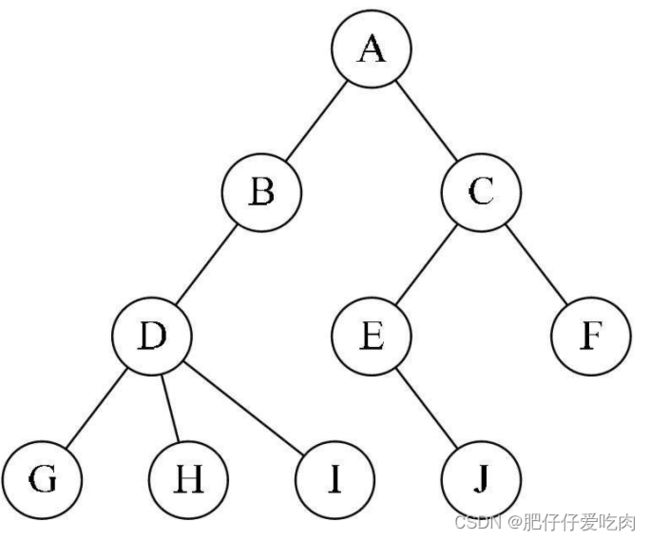
由于根结点是没有双亲的, 所以我们约定根结点的位置域设置为-1,这也就意味着,我们所有的结点都存有它双亲的位置。如图的树结构:
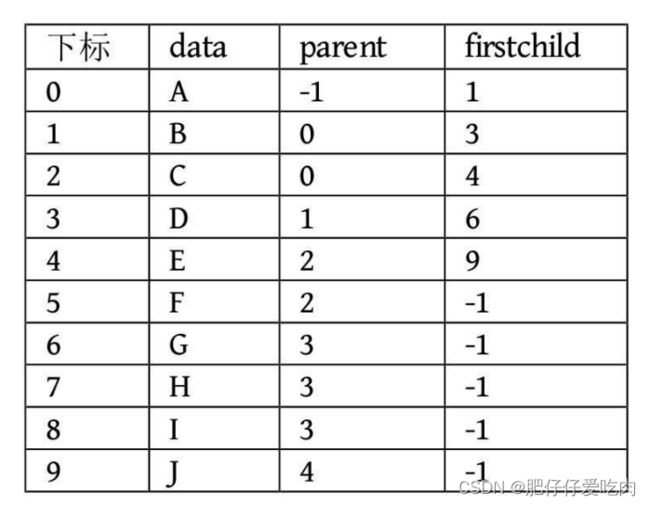
我们可以根据结点的parent指针很容易找到它的双亲结点,所用的时间复杂度为O(1),直到parent为-1时,表示找到了树结点的根。我们增加一个结点最左边孩子的域,不妨叫它长子域,这样就可以很容易得到结点的孩子。如果没有孩子的结点,这个长子域就设置为-1,如表所示。
2.2孩子表示法:
每个结点指针域的个数等于该结点的度,我们专门取一个位置来存储结点 指针域的个数,其结构如表所示。
其中data为数据域,degree为度域,也就是存储该结点的孩子结点的个数,child1到 childd为指针域,指向该结点的各个孩子的结点。
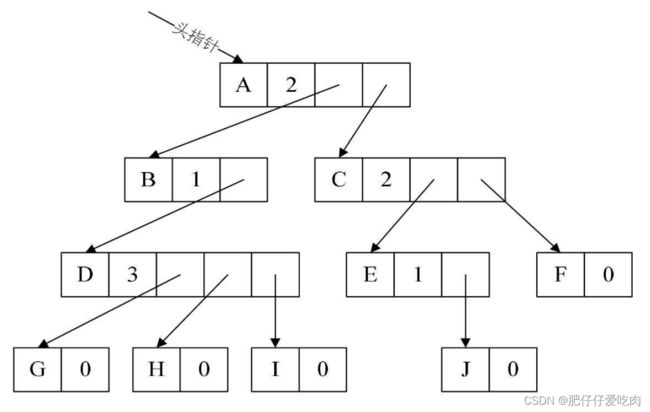
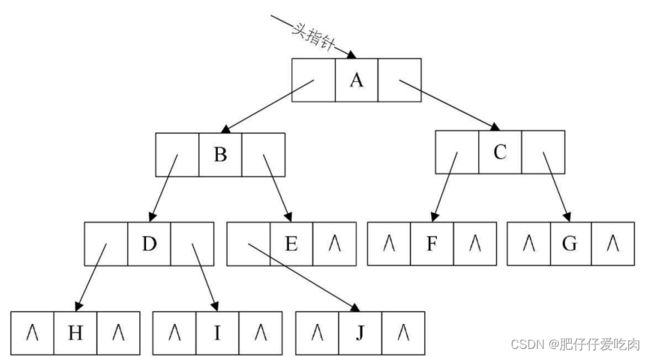
把每个结点的孩子结点排列起来,以单 链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后 n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中,如图所示。
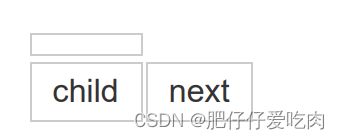
设计两种结点结构,一个是孩子链表的孩子结点,如表所示。
其中child是数据域,用来存储某个结点在表头数组中的下标。next是指针域,用来存 储指向某结点的下一个孩子结点的指针。
另一个是表头数组的表头结点,如表所示。
其中data是数据域,存储某结点的数据信息。firstchild是头指针域,存储该结点的孩 子链表的头指针。
代码如下:
#define MAX_TREE_SIZE 100
/* 孩子结点 */
typedef struct CTNode
{
int child;
struct CTNode* next;
} *ChildPtr;
/* 表头结构 */
typedef struct
{
TElemType data;
ChildPtr firstchild;
} CTBox;
/* 树结构 */
typedef struct
{
/* 结点数组 */
CTBox nodes[MAX_TREE_SIZE];
/* 根的位置和结点数 */
int r, n;
} CTree;
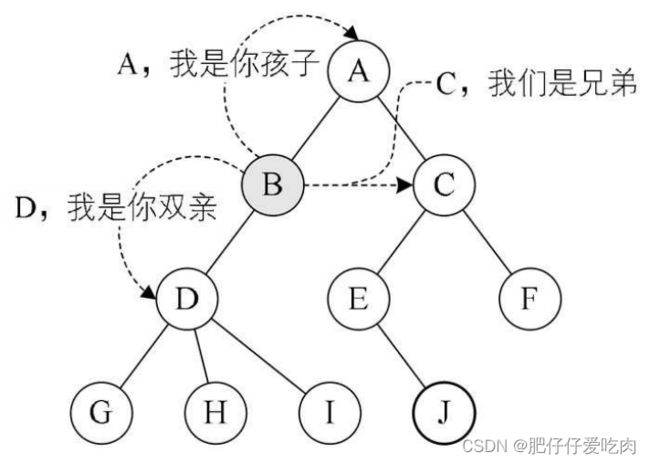
2.3孩子兄弟表示法:
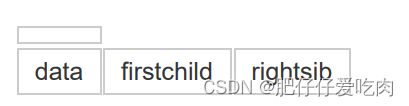
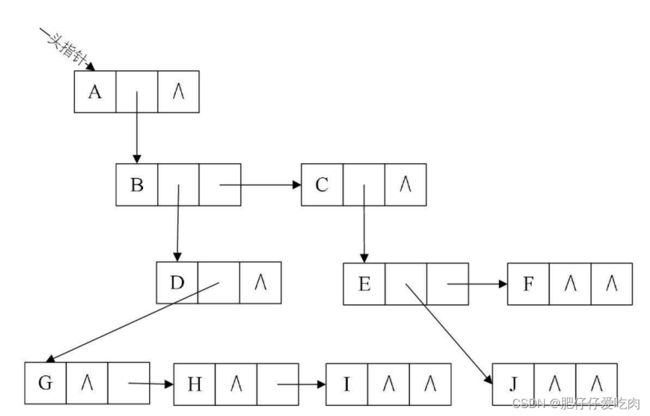
从树结点的兄弟的角度考虑,设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
其中data是数据域,firstchild为指针域,存储该结点的第一个孩子结点的存储地址, right-sib是指针域,存储该结点的右兄弟结点的存储地址。
代码如下:
/* 树的孩子兄弟表示法结构定义 */
typedef struct CSNode
{
TElemType data;
struct CSNode* firstchild,
* rightsib;
} CSNode, * CSTree;示意图:
二、二叉树
1.二叉树的定义
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集台或者为空集(称为空二叉树)或者由一个根结点和两棵互不相交的、分别称为根结点的左子树租石子树的二叉树组成。
2.二叉树的特点
特点:
- 每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。注意不是只有两棵子树,而是最多有。没有子树或者有一棵子树都是可以的。
- 左子树和右子树是有顺序的,次序不能任意颠倒。就像人有双手、双脚,但显然左手、左脚和右手、右脚是不一样的,右手戴左手套、右脚穿左鞋都会极其别扭和难受。
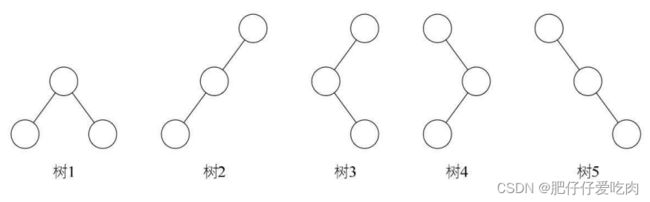
- 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。下图树1 和树2是同一棵树,但它们却是不同的二叉树。就好像你一不小心,摔伤了手,伤的是左手还是右手,对你的生活影响度是完全不同的。
二叉树具有五种基本形态:
1.空二叉树。
2.只有一个根结点。
3.根结点只有左子树。
4.根结点只有右子树。
5.根结点既有左子树又有右子树。
应该说这五种形态还是比较好理解的,那我现在问大家,如果是有三个结点的树,有几种形态?如果是有三个结点的二叉树,考虑一下,又有几种形态?
若只从形态上考虑,三个结点的树只有两种情况,那就是下图中有两层的树1和有三层的后四种的任意一种,但对于二叉树来说,由于要区分左右,所以就演变成五种形态,树2、树3、树4和树5分别代表不同的二叉树。
3.特殊二叉树
3.1斜树:
顾名思义,斜树一定要是斜的,但是往哪斜还是有讲究。所有的结点都只有左子树的 二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。 上图树2就是左斜树,树5就是右斜树。斜树有很明显的特点,就是每一层都只有一个结点,结点的个数与二叉树的深度相同。
4.2满二叉树:
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
单是每个结点都存在左右子树,不能算是满二叉树,还必须要所有的叶子都在同一层上,这就做到了整棵树的平衡。因此,满二叉树的特点有:
(1)叶子只能出现在最下一层。出现在其他层就不可能达成平衡。
(2)非叶子结点的度一定是2。否则就 是“缺胳膊少腿”了。
(3)在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
4.3完全二叉树:
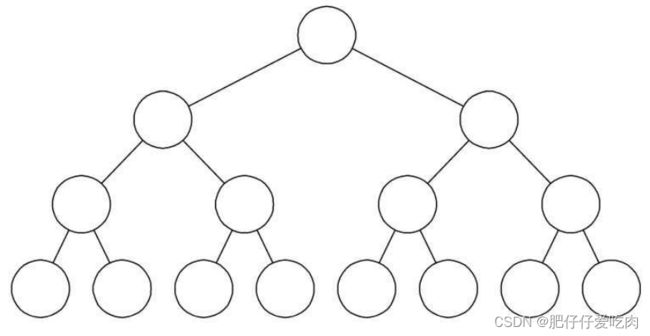
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的 满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
这是一种有些理解难度的特殊二叉树。
首先从字面上要区分,“完全”和“满”的差异,满二叉树一定是一棵完全二叉树,但完全二叉树不一定是满的。
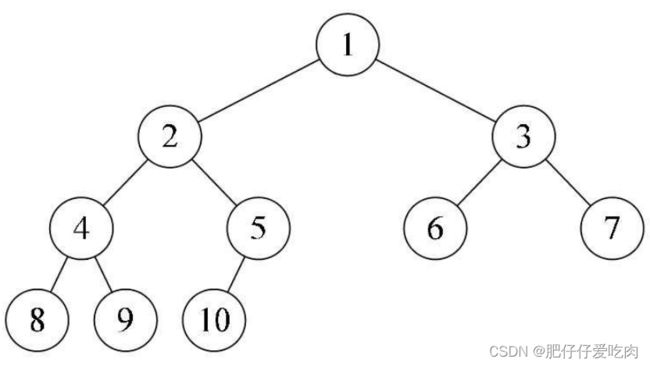
其次,完全二叉树的所有结点与同样深度的满二叉树,它们按层序编号相同的结点是一一对应的。这里有个关键词是按层序编号,像下图中的树,因为5结点没有左子树,却有右子树,那就使得按层序编号的第10个编号空档了,它不是完全二叉树。
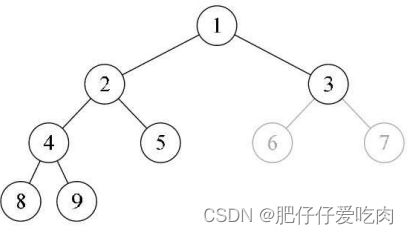
同样道理,下图中的树,由于结点3没有子树,所以使得6、7编号的位置空档了。它不是完全二叉树。
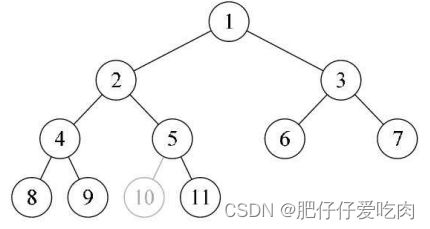
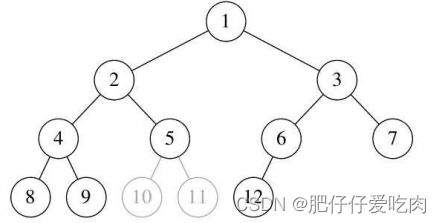
下图中的树又是因为5编号下没有子树造成第10和第11位置空挡。它也不是完全二叉树。
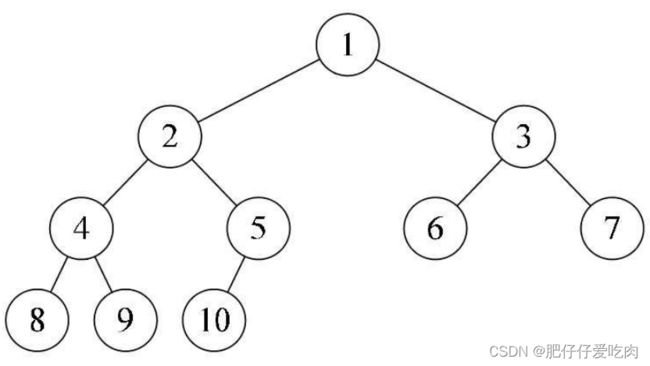
只有下图中的树,尽管它不是满二叉树,但是编号是连续的,所以它是完全二叉树。
从这里我也可以得出一些完全二叉树的特点:
(1)叶子结点只能出现在最下两层。
(2)最下层的叶子一定集中在左部连续位置。
(3)倒数二层,若有叶子结点,一定 都在右部连续位置。
(4)如果结点度为1,则该结点只有左孩子,即不存在只有右子 树的情况。
(5)同样结点数的二叉树,完全二叉树的深度最小。
从上面的例子,也给了我们一个判断某二叉树是否是完全二叉树的办法,那就是看着树的示意图,心中默默给每个结点按照满二叉树的结构逐层顺序编号,如果编号出现空档,就说明不是完全二叉树,否则就是。
4.二叉树的性质
性质1:在二叉树的第i层上至多有2 i-1个结点(i≥1)。
性质2:深度为k的二叉树至多有2^k -1个结点(k≥1)。
性质3:对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则 n0=n2+1。
性质4:具有n个结点的完全二叉树的深度为|log2n+1|(|x|表示不大于x的最大整数)。
性质5:如果对一棵有n个结点的完全二叉树(其深度为)的结点按层序编号(从第1 层到第层,每层从左到右),对任一结点i(1≤i≤n)有:
(1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点。
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
5.二叉树的存储结构
5.1顺序存储
二叉树是一种特殊的树,由于它的特殊性,使得用顺序存储结构也可以实现。
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置, 也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。
一般的二叉树,注意浅色结点表示不存在。
将这棵二叉树存入到数组中,相应的下标对应其同样的位置,如图所示。
5.2 二叉链表
顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。结点结构图如表6-7-1所示。
其中data是数据域,lchild和rchild都是指针域,分别存放指向左孩子和右孩子的指针。
二叉链表的结点结构定义代码:
/* 二叉树的二叉链表结点结构定义 */
/* 结点结构 */
typedef struct BiTNode
{
/* 结点数据 */
TElemType data;
/* 左右孩子指针 */
struct BiTNode* lchild, * rchild;
} BiTNode, * BiTree;结构示意图:
6.二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二 叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
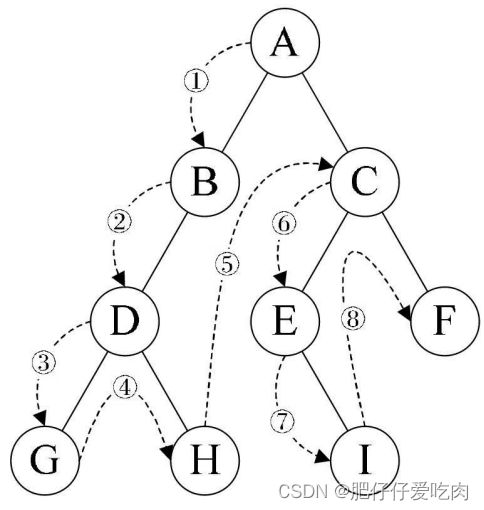
6.1前序遍历:
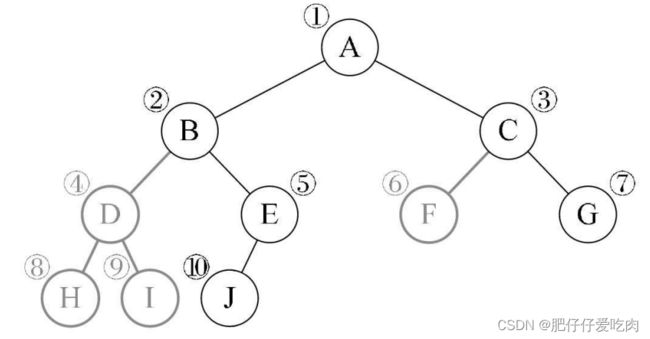
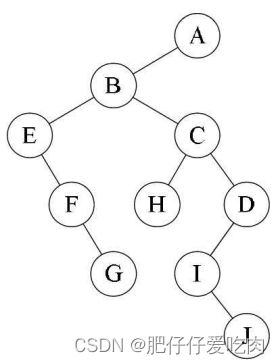
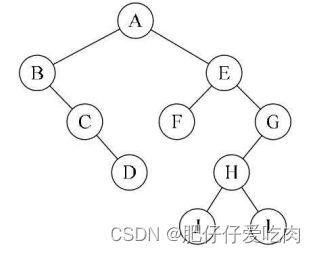
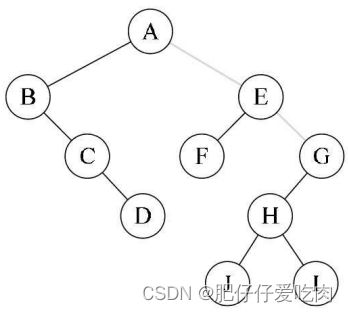
规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。如图所示,遍历的顺序为:ABDGH-CEIF。
二叉树的前序遍历算法。代码如下:
/* 二叉树的前序遍历递归算法 */
void PreOrderTraverse(BiTree T)
{
if (T == NULL)
return;
/* 显示结点数据,可以更改为其他对结点操作 */
printf("%c", T->data);
/* 再先序遍历左子树 */
PreOrderTraverse(T->lchild);
/* 最后先序遍历右子树 */
PreOrderTraverse(T->rchild);
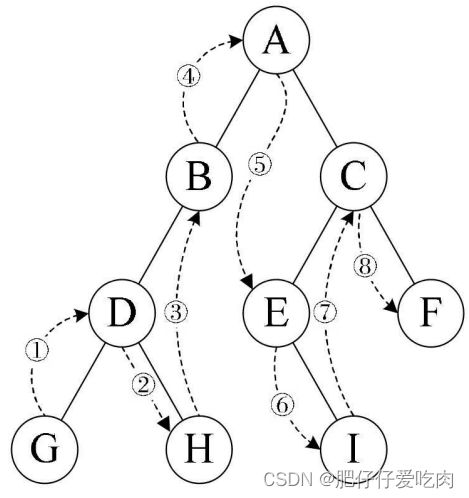
}6.2中序遍历:
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点), 中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。如图所示,遍历的顺序为:GDHBAE-ICF。
二叉树的中序遍历递归算法。代码如下:
/* 二叉树的中序遍历递归算法 */
void InOrderTraverse(BiTree T)
{
if (T == NULL)
return;
/* 中序遍历左子树 */
InOrderTraverse(T->lchild);
/* 显示结点数据,可以更改为其他对结点操作 */
printf("%c", T->data);
/* 最后中序遍历右子树 */
InOrderTraverse(T->rchild);
}
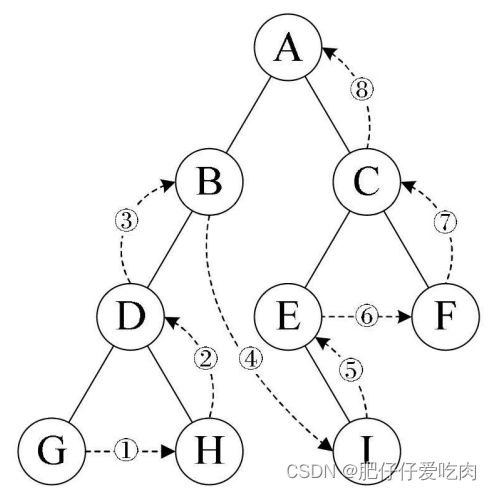
6.3后序遍历:
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。如图所示,遍历的顺序为:GHDBIEFCA。
二叉树的后序遍历递归算法。代码如下:
/* 二叉树的后序遍历递归算法 */
void PostOrderTraverse(BiTree T)
{
if (T == NULL)
return;
/* 先后序遍历左子树 */
PostOrderTraverse(T->lchild);
/* 再后序遍历右子树 */
PostOrderTraverse(T->rchild);
/* 显示结点数据,可以更改为其他对结点操作 */
printf("%c", T->data);
}
6.4层序遍历:
规则是若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。如图所示,遍历的顺序为:ABCDEFGHI。
6.5推导遍历:
下面是推导的前提条件:
- 已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
- 已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
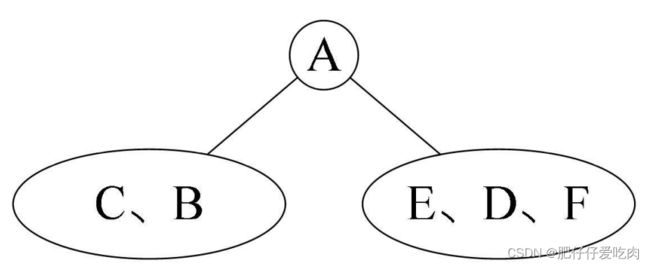
例:前序遍历序列为ABCDEF,中序遍历序列为CBAEDF,求这棵二叉树的后序遍历是?
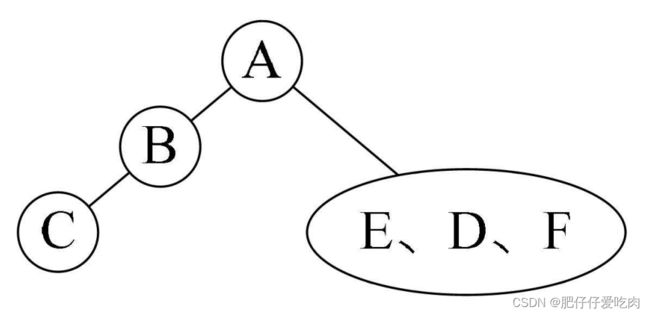
前序遍历序列为 ABCDEF,第一个字母是A被打印出来,就说明A是根结点的数据。再由中序遍历序列 是CBAEDF,可以知道C和B是A的左子树的结点,E、D、F是A的右子树的结点。
然后我们看前序中的C和B,它的顺序是ABCDEF,是先打印B后打印C,所以B应该是A的左孩子,而C就只能是B的孩子,此时是左还是右孩子还不确定。再看中序序列是CBAEDF,C是在B的前面打印,这就说明C是B的左孩子,否则就是右孩子了。
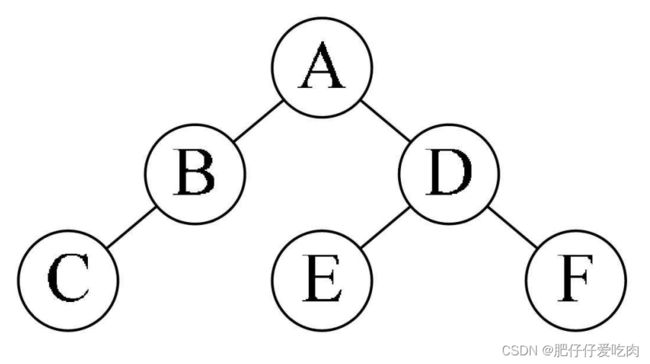
再看前序中的E、D、F,它的顺序是ABCDEF,那就意味着D是A结点的右孩子,E和 F是D的子孙,注意,它们中有一个不一定是孩子,还有可能是孙子的。再来看中序序列是CBAEDF,由于E在D的左侧,而F在右侧,所以可以确定E是D的左孩子,F是D 的右孩子。因此最终得到的二叉树。
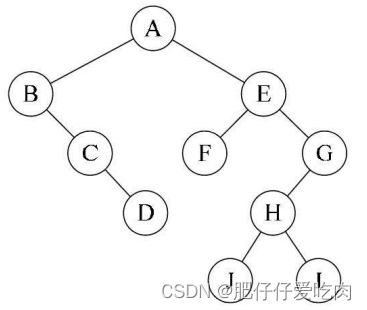
7.二叉树的建立
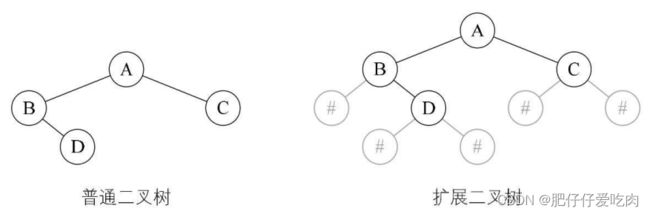
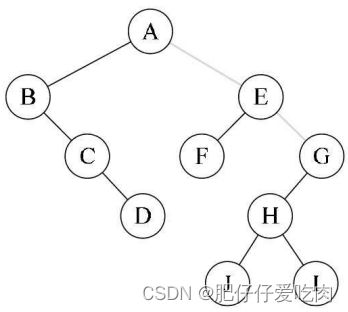
建立一个如左图这样的树,为了能让每个结点确认是否有左右孩子,我们对它进行了扩展,变成右图的样子,也就是将二叉树中每个结点的空指针引出一个虚结点,其值为一特定值,比如“#”。
我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定一棵二叉树了。 比下图扩展二叉树的前序遍历序列就为AB#D##C##。
有了这样的准备,我们就可以来看看如何生成一棵二叉树了。假设二叉树的结点均为一个字符,我们把刚才前序遍历序列AB#D##C##用键盘挨个输入。实现的算法如下:
/* 按前序输入二叉树中结点的值(一个字符) */
/* #表示空树,构造二叉链表表示二叉树T。 */
void CreateBiTree(BiTree* T)
{
TElemType ch;
scanf("%c", &ch);
if (ch == '#')
*T = NULL;
else
{
*T = (BiTree)malloc(sizeof(BiTNode));
if (!*T)
exit(OVERFLOW);
/* 生成根结点 */
(*T)->data = ch;
/* 构造左子树 */
CreateBiTree(&(*T)->lchild);
/* 构造右子树 */
CreateBiTree(&(*T)->rchild);
}
}其实建立二叉树,也是利用了递归的原理。只不过在原来应该是打印结点的地方,改成了生成结点、给结点赋值的操作而已。
三、树、深林、二叉树的转换
在树的存储结构时,我们了解到树的孩子兄弟法可以将一棵树用二叉链表进行存储,所以借助二叉链表,树和二叉树可以相互进行转换。
因此,只要我们设定一定的规则,用二叉树来表示树,甚至表示森林都是可以的,森林与二叉树也可以互相进行转换。
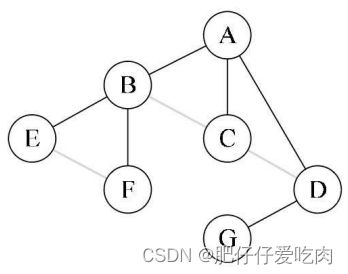
1. 树转换为二叉树
树:
步骤如下:
1)加线。在所有兄弟结点之间加一条连线。
2)去线。对树中每个结点,只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
3)层次调整。以树的根结点为轴心,将整棵树顺时针旋转一定的角度,使之结构层次分明。注意第一个孩子是二叉树结点的左孩子,兄弟转换过来的孩子是结点的右孩子。一棵树经过三个步骤转换为一棵二叉树。
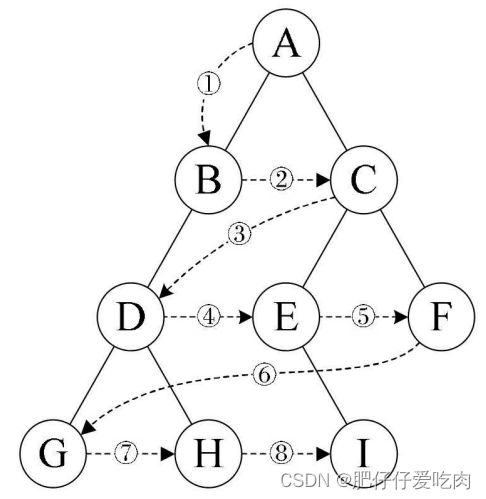
2.森林转换为二叉树
森林是由若干棵树组成的,所以可以理解为,森林中的每一棵树都是兄弟,可以按照兄弟的处理办法来操作。
三棵树:
转换步骤如下:
1)把每个树转换为二叉树。
2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树。 此时森林的三棵树转化为一棵二叉树。
3 .二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,也就是反过来做而已。
步骤如下:
1)加线。若某结点的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点……哈,反正就是左孩子的 n个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接起来。
2)去线。删除原二叉树中所有结点与其右孩子结点的连线。
3)层次调整。使之结构层次分明。
4. 二叉树转换为森林
判断一棵二叉树能够转换成一棵树还是森林,标准很简单,那就是只要看这棵二叉树的根结点有没有右孩子,有就是森林,没有就是一棵树。
步骤如下:
1)从根结点开始,若右孩子存在,则把与右孩子结点的连线删除,再查看分离后的二叉树,若右孩子存在,则连线删除……,直到所有右孩子连线都删除为止, 得到分离的二叉树。
2)再将每棵分离后的二叉树转换为树即可。
5.树与森林的遍历
5.1树的遍历分为两种方式。
1)一种是先根遍历树,即先访问树的根结点,然后依次先根遍历根的每棵子树。
2)另一种是后根遍历,即先依次后根遍历每棵子树,然后再访问根结点。
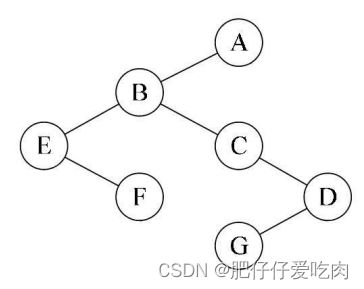
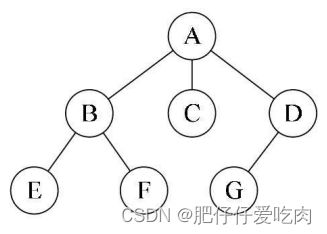
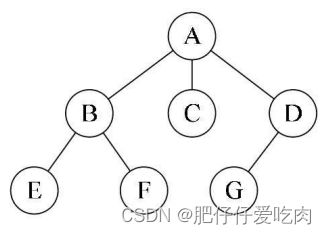
例图:
先根遍历序列为ABEFCDG,后根遍历序列为EFBCGDA。
5.2森林的遍历也分为两种方式:
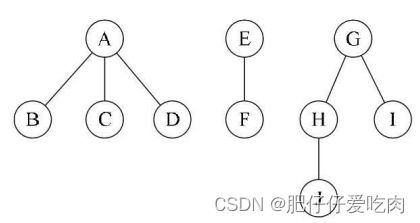
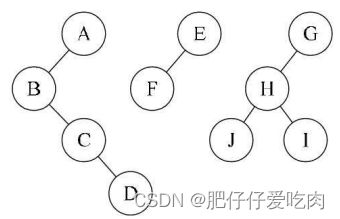
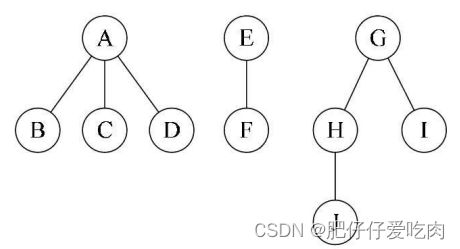
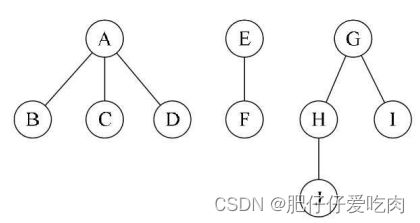
1)前序遍历:先访问森林中第一棵树的根结点,然后再依次先根遍历根的每棵子树,再依次用同样方式遍历除去第一棵树的剩余树构成的森林。例如下面三棵树的森林,前序遍历序列的结果就是ABCDEFGHJI。
2)后序遍历:是先访问森林中第一棵树,后根遍历的方式遍历每棵子树,然后再访问根结点,再依次同样方式遍历除去第一棵树的剩余树构成的森林。比如下面三棵树的森林,后序遍历序列的结果就是BCDAFEJHIG。
参考:
- 程杰:《大话数据结构》
- 石田保辉:《我的第一本算法书》
- 渡部有隆:《挑战程序设计竞赛2》
附录1:二叉树顺序结构实现
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
#define MAX_TREE_SIZE 100 /* 二叉树的最大结点数 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int TElemType; /* 树结点的数据类型,目前暂定为整型 */
typedef TElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根结点 */
typedef struct
{
int level,order; /* 结点的层,本层序号(按满二叉树计算) */
}Position;
TElemType Nil=0; /* 设整型以0为空 */
Status visit(TElemType c)
{
printf("%d ",c);
return OK;
}
/* 构造空二叉树T。因为T是固定数组,不会改变,故不需要& */
Status InitBiTree(SqBiTree T)
{
int i;
for(i=0;i=0;i--) /* 找到最后一个结点 */
if(T[i]!=Nil)
break;
i++;
do
j++;
while(i>=powl(2,j));/* 计算2的j次幂。 */
return j;
}
/* 初始条件: 二叉树T存在 */
/* 操作结果: 当T不空,用e返回T的根,返回OK;否则返回ERROR,e无定义 */
Status Root(SqBiTree T,TElemType *e)
{
if(BiTreeEmpty(T)) /* T空 */
return ERROR;
else
{
*e=T[0];
return OK;
}
}
/* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */
/* 操作结果: 返回处于位置e(层,本层序号)的结点的值 */
TElemType Value(SqBiTree T,Position e)
{
return T[(int)powl(2,e.level-1)+e.order-2];
}
/* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */
/* 操作结果: 给处于位置e(层,本层序号)的结点赋新值value */
Status Assign(SqBiTree T,Position e,TElemType value)
{
int i=(int)powl(2,e.level-1)+e.order-2; /* 将层、本层序号转为矩阵的序号 */
if(value!=Nil&&T[(i+1)/2-1]==Nil) /* 给叶子赋非空值但双亲为空 */
return ERROR;
else if(value==Nil&&(T[i*2+1]!=Nil||T[i*2+2]!=Nil)) /* 给双亲赋空值但有叶子(不空) */
return ERROR;
T[i]=value;
return OK;
}
/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 若e是T的非根结点,则返回它的双亲,否则返回"空" */
TElemType Parent(SqBiTree T,TElemType e)
{
int i;
if(T[0]==Nil) /* 空树 */
return Nil;
for(i=1;i<=MAX_TREE_SIZE-1;i++)
if(T[i]==e) /* 找到e */
return T[(i+1)/2-1];
return Nil; /* 没找到e */
}
/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的左孩子。若e无左孩子,则返回"空" */
TElemType LeftChild(SqBiTree T,TElemType e)
{
int i;
if(T[0]==Nil) /* 空树 */
return Nil;
for(i=0;i<=MAX_TREE_SIZE-1;i++)
if(T[i]==e) /* 找到e */
return T[i*2+1];
return Nil; /* 没找到e */
}
/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的右孩子。若e无右孩子,则返回"空" */
TElemType RightChild(SqBiTree T,TElemType e)
{
int i;
if(T[0]==Nil) /* 空树 */
return Nil;
for(i=0;i<=MAX_TREE_SIZE-1;i++)
if(T[i]==e) /* 找到e */
return T[i*2+2];
return Nil; /* 没找到e */
}
/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回"空" */
TElemType LeftSibling(SqBiTree T,TElemType e)
{
int i;
if(T[0]==Nil) /* 空树 */
return Nil;
for(i=1;i<=MAX_TREE_SIZE-1;i++)
if(T[i]==e&&i%2==0) /* 找到e且其序号为偶数(是右孩子) */
return T[i-1];
return Nil; /* 没找到e */
}
/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回"空" */
TElemType RightSibling(SqBiTree T,TElemType e)
{
int i;
if(T[0]==Nil) /* 空树 */
return Nil;
for(i=1;i<=MAX_TREE_SIZE-1;i++)
if(T[i]==e&&i%2) /* 找到e且其序号为奇数(是左孩子) */
return T[i+1];
return Nil; /* 没找到e */
}
/* PreOrderTraverse()调用 */
void PreTraverse(SqBiTree T,int e)
{
visit(T[e]);
if(T[2*e+1]!=Nil) /* 左子树不空 */
PreTraverse(T,2*e+1);
if(T[2*e+2]!=Nil) /* 右子树不空 */
PreTraverse(T,2*e+2);
}
/* 初始条件: 二叉树存在 */
/* 操作结果: 先序遍历T。 */
Status PreOrderTraverse(SqBiTree T)
{
if(!BiTreeEmpty(T)) /* 树不空 */
PreTraverse(T,0);
printf("\n");
return OK;
}
/* InOrderTraverse()调用 */
void InTraverse(SqBiTree T,int e)
{
if(T[2*e+1]!=Nil) /* 左子树不空 */
InTraverse(T,2*e+1);
visit(T[e]);
if(T[2*e+2]!=Nil) /* 右子树不空 */
InTraverse(T,2*e+2);
}
/* 初始条件: 二叉树存在 */
/* 操作结果: 中序遍历T。 */
Status InOrderTraverse(SqBiTree T)
{
if(!BiTreeEmpty(T)) /* 树不空 */
InTraverse(T,0);
printf("\n");
return OK;
}
/* PostOrderTraverse()调用 */
void PostTraverse(SqBiTree T,int e)
{
if(T[2*e+1]!=Nil) /* 左子树不空 */
PostTraverse(T,2*e+1);
if(T[2*e+2]!=Nil) /* 右子树不空 */
PostTraverse(T,2*e+2);
visit(T[e]);
}
/* 初始条件: 二叉树T存在 */
/* 操作结果: 后序遍历T。 */
Status PostOrderTraverse(SqBiTree T)
{
if(!BiTreeEmpty(T)) /* 树不空 */
PostTraverse(T,0);
printf("\n");
return OK;
}
/* 层序遍历二叉树 */
void LevelOrderTraverse(SqBiTree T)
{
int i=MAX_TREE_SIZE-1,j;
while(T[i]==Nil)
i--; /* 找到最后一个非空结点的序号 */
for(j=0;j<=i;j++) /* 从根结点起,按层序遍历二叉树 */
if(T[j]!=Nil)
visit(T[j]); /* 只遍历非空的结点 */
printf("\n");
}
/* 逐层、按本层序号输出二叉树 */
void Print(SqBiTree T)
{
int j,k;
Position p;
TElemType e;
for(j=1;j<=BiTreeDepth(T);j++)
{
printf("第%d层: ",j);
for(k=1;k<=powl(2,j-1);k++)
{
p.level=j;
p.order=k;
e=Value(T,p);
if(e!=Nil)
printf("%d:%d ",k,e);
}
printf("\n");
}
}
int main()
{
Status i;
Position p;
TElemType e;
SqBiTree T;
InitBiTree(T);
CreateBiTree(T);
printf("建立二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
i=Root(T,&e);
if(i)
printf("二叉树的根为:%d\n",e);
else
printf("树空,无根\n");
printf("层序遍历二叉树:\n");
LevelOrderTraverse(T);
printf("前序遍历二叉树:\n");
PreOrderTraverse(T);
printf("中序遍历二叉树:\n");
InOrderTraverse(T);
printf("后序遍历二叉树:\n");
PostOrderTraverse(T);
printf("修改结点的层号3本层序号2。");
p.level=3;
p.order=2;
e=Value(T,p);
printf("待修改结点的原值为%d请输入新值:50 ",e);
e=50;
Assign(T,p,e);
printf("前序遍历二叉树:\n");
PreOrderTraverse(T);
printf("结点%d的双亲为%d,左右孩子分别为",e,Parent(T,e));
printf("%d,%d,左右兄弟分别为",LeftChild(T,e),RightChild(T,e));
printf("%d,%d\n",LeftSibling(T,e),RightSibling(T,e));
ClearBiTree(T);
printf("清除二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
i=Root(T,&e);
if(i)
printf("二叉树的根为:%d\n",e);
else
printf("树空,无根\n");
return 0;
}
附录2:二叉树链式结构实现
#include "string.h"
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
/* 用于构造二叉树********************************** */
int treeIndex=1;
typedef char String[24]; /* 0号单元存放串的长度 */
String str;
Status StrAssign(String T,char *chars)
{
int i;
if(strlen(chars)>MAXSIZE)
return ERROR;
else
{
T[0]=strlen(chars);
for(i=1;i<=T[0];i++)
T[i]=*(chars+i-1);
return OK;
}
}
/* ************************************************ */
typedef char TElemType;
TElemType Nil=' '; /* 字符型以空格符为空 */
Status visit(TElemType e)
{
printf("%c ",e);
return OK;
}
typedef struct BiTNode /* 结点结构 */
{
TElemType data; /* 结点数据 */
struct BiTNode *lchild,*rchild; /* 左右孩子指针 */
}BiTNode,*BiTree;
/* 构造空二叉树T */
Status InitBiTree(BiTree *T)
{
*T=NULL;
return OK;
}
/* 初始条件: 二叉树T存在。操作结果: 销毁二叉树T */
void DestroyBiTree(BiTree *T)
{
if(*T)
{
if((*T)->lchild) /* 有左孩子 */
DestroyBiTree(&(*T)->lchild); /* 销毁左孩子子树 */
if((*T)->rchild) /* 有右孩子 */
DestroyBiTree(&(*T)->rchild); /* 销毁右孩子子树 */
free(*T); /* 释放根结点 */
*T=NULL; /* 空指针赋0 */
}
}
/* 按前序输入二叉树中结点的值(一个字符) */
/* #表示空树,构造二叉链表表示二叉树T。 */
void CreateBiTree(BiTree *T)
{
TElemType ch;
/* scanf("%c",&ch); */
ch=str[treeIndex++];
if(ch=='#')
*T=NULL;
else
{
*T=(BiTree)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data=ch; /* 生成根结点 */
CreateBiTree(&(*T)->lchild); /* 构造左子树 */
CreateBiTree(&(*T)->rchild); /* 构造右子树 */
}
}
/* 初始条件: 二叉树T存在 */
/* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */
Status BiTreeEmpty(BiTree T)
{
if(T)
return FALSE;
else
return TRUE;
}
#define ClearBiTree DestroyBiTree
/* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */
int BiTreeDepth(BiTree T)
{
int i,j;
if(!T)
return 0;
if(T->lchild)
i=BiTreeDepth(T->lchild);
else
i=0;
if(T->rchild)
j=BiTreeDepth(T->rchild);
else
j=0;
return i>j?i+1:j+1;
}
/* 初始条件: 二叉树T存在。操作结果: 返回T的根 */
TElemType Root(BiTree T)
{
if(BiTreeEmpty(T))
return Nil;
else
return T->data;
}
/* 初始条件: 二叉树T存在,p指向T中某个结点 */
/* 操作结果: 返回p所指结点的值 */
TElemType Value(BiTree p)
{
return p->data;
}
/* 给p所指结点赋值为value */
void Assign(BiTree p,TElemType value)
{
p->data=value;
}
/* 初始条件: 二叉树T存在 */
/* 操作结果: 前序递归遍历T */
void PreOrderTraverse(BiTree T)
{
if(T==NULL)
return;
printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */
PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
}
/* 初始条件: 二叉树T存在 */
/* 操作结果: 中序递归遍历T */
void InOrderTraverse(BiTree T)
{
if(T==NULL)
return;
InOrderTraverse(T->lchild); /* 中序遍历左子树 */
printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
}
/* 初始条件: 二叉树T存在 */
/* 操作结果: 后序递归遍历T */
void PostOrderTraverse(BiTree T)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild); /* 先后序遍历左子树 */
PostOrderTraverse(T->rchild); /* 再后序遍历右子树 */
printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
}
int main()
{
int i;
BiTree T;
TElemType e1;
InitBiTree(&T);
StrAssign(str,"ABDH#K###E##CFI###G#J##");
CreateBiTree(&T);
printf("构造空二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
e1=Root(T);
printf("二叉树的根为: %c\n",e1);
printf("\n前序遍历二叉树:");
PreOrderTraverse(T);
printf("\n中序遍历二叉树:");
InOrderTraverse(T);
printf("\n后序遍历二叉树:");
PostOrderTraverse(T);
ClearBiTree(&T);
printf("\n清除二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
i=Root(T);
if(!i)
printf("树空,无根\n");
return 0;
}