刷题记录(自己看的习题本)(74_11.30)
杂
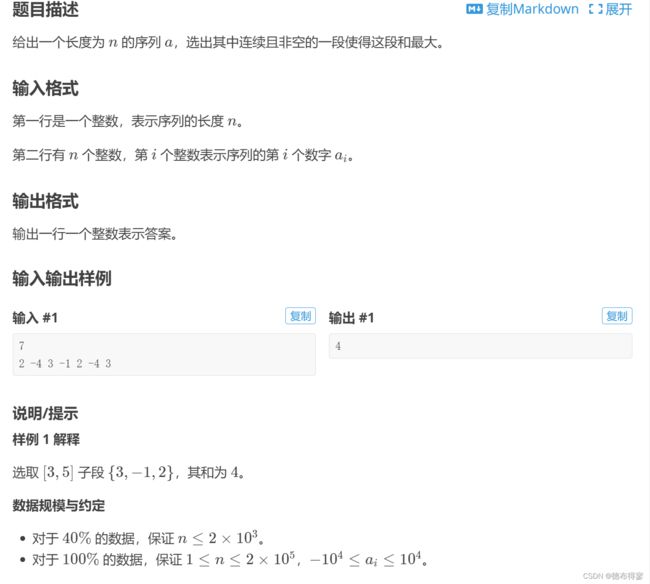
区间和(离散化)
题目链接:802. 区间和 - AcWing题库
#include
#include
#include
using namespace std;
const int N = 300010; //n次插入和m次查询相关数据量的上界
int n, m;
int a[N];//存储坐标插入的值
int s[N];//存储数组a的前缀和
vector alls; //存储(所有与插入和查询有关的)坐标
vector> add, query; //存储插入和询问操作的数据
int find(int x) { //返回的是输入的坐标的离散化下标
int l = 0, r = alls.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int x, c;
scanf("%d%d", &x, &c);
add.push_back({x, c});
alls.push_back(x);
}
for (int i = 1; i <= m; i++) {
int l , r;
scanf("%d%d", &l, &r);
query.push_back({l, r});
alls.push_back(l);
alls.push_back(r);
}
//排序,去重
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
//执行前n次插入操作
for (auto item : add) {
int x = find(item.first);
a[x] += item.second;
}
//前缀和
for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];
//处理后m次询问操作
for (auto item : query) {
int l = find(item.first);
int r = find(item.second);
printf("%d\n", s[r] - s[l-1]);
}
return 0;
}
/*作者:liangshang
链接:https://www.acwing.com/solution/content/13511/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。*/ 区间合并(区间合并)
题目链接:803. 区间合并 - AcWing题库
问题:给出多个区间,合并有交集的区间,最后得出剩余的单独区间有多少个。
思路:
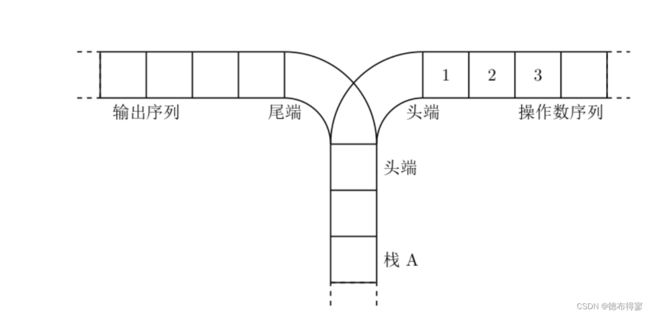
用维护左右端点的数据typedef pair
区间之间分为3种情况:完全没有交集,完全合并为一个大区间,有交集。
对vector
维护一个区间,每次这个区间对比下一个区间的3种情况。没有交集就存入vector
#include
#include
#include
using namespace std;
typedef pair PII;
void merge(vector &segs) //模版
{
vector res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;
for (auto seg : segs)
if (ed < seg.first)
{
if (st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
else ed = max(ed, seg.second);
if (st != -2e9) res.push_back({st, ed});
segs = res;
}
int main()
{
int n;
scanf("%d", &n);
vector segs;
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
segs.push_back({l, r});
}
merge(segs);
cout << segs.size() << endl;
return 0;
}
数学
2582. 递枕头(模拟)(数学)
问题描述:
n 个人站成一排,按从 1 到 n 编号。
最初,排在队首的第一个人拿着一个枕头。每秒钟,拿着枕头的人会将枕头传递给队伍中的下一个人。一旦枕头到达队首或队尾,传递方向就会改变,队伍会继续沿相反方向传递枕头。
- 例如,当枕头到达第
n个人时,TA 会将枕头传递给第n - 1个人,然后传递给第n - 2个人,依此类推。
给你两个正整数 n 和 time ,返回 time 秒后拿着枕头的人的编号。
思路:暴力模拟或者数学找规律
class Solution {
public:
int passThePillow(int n, int time) {
/*找规律*/
time %= (n - 1) * 2;
return time < n ? time + 1 : n * 2 - time - 1;
}
};
/*
模拟:
int ans = 1, k = 1;
while (time--) {
ans += k;
if (ans == 1 || ans == n) {
k *= -1;
}
}
return ans;
*/
AcWing 868. 筛质数(数学)(筛质数)
问题描述:给一个数n,筛出1到n里所有的质数的个数
思路与理解:
1.朴素:从2开始,筛出每个2的倍数,比如4,6,8,10.再从3开始筛出每个3的倍数,6,9,12,
代码:
#include
#include
using namespace std;
const int N= 1000010;
int primes[N], cnt;
bool st[N];
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
int main()
{
int n;
cin >> n;
get_primes(n);
cout << cnt << endl;
return 0;
}
蛇形填数(数学)
题目链接:蛇形填数 - 蓝桥云课 (lanqiao.cn)
题解:(蓝桥杯填空题原题)这个题就是个找规律题。根据题目提示找到数与数之间的规律。
2020年第十一届蓝桥杯 - 省赛 - C/C++大学生A组 - C.蛇形填数_哔哩哔哩_bilibili
代码:
#include
using namespace std;
int main()
{
int n=20,ans=1;
for (int i=0;i P2241 统计方形(数学)
描述:给一个n * m 的矩形,得出这个矩形里面有多少个正方形和长方形
代码:
#include
using namespace std;
long long n,m,rec,sqr;
int main() {
cin>>n>>m;
for(int i=0; i 详细理解见:P2241 统计方形(数据加强版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
此类数学题 遇到了就会,没遇到就不会。当公式记住了
if(i==j) sqr+=(n-i)*(m-j);//如果i==j,说明是正方形
else rec+=(n-i)*(m-j);//如果不等说明是矩形
bhq的小物块(数学)
链接:L-bhq的小物块_第五届山东师范大学与齐鲁工业大学ICPC新生联谊赛 (nowcoder.com)
代码:
#include
using namespace std;
typedef long long int64;
const double PI = M_PI;
void solve(){
int n;
cin >> n;
cout << (int64)(PI * pow(10L, n)) << endl;
}
int main(){
int t;
cin >> t;
while(t-- > 0) solve();
} 学习了:
1.pow(10L, n)
表示10的n次方,10L 的 L 表示这个10是 long 型的
2.库里面的pi值 const double PI = M_PI;
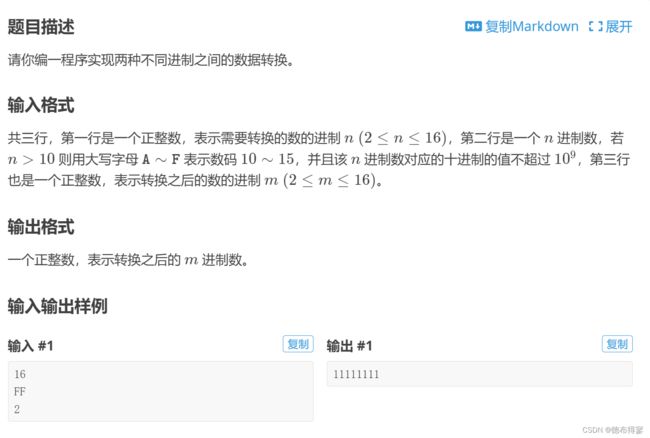
P1143 进制转换
链接:P1143 进制转换 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
using namespace std;
string a;
int c[10000000],d,e,f,g,sum,ans;
int main()
{
scanf("%d",&d);
cin>>a;
scanf("%d",&f);
/*for(int x=0;x0){
c[g++]=sum%f;
sum/=f; //sum(10进制)转换成f进制
}
for(int x=g-1;x>=0;x--){
if(c[x]>=10)printf("%c",c[x]+'A'-10);
else printf("%d",c[x]);
}
return 0;
} 学习的都在代码里面了:
1. sum=stoi(a,NULL,d); //d进制转换成10进制
2.
//sum(10进制)转换成f进制
while(sum>0){
c[g++]=sum%f;
sum/=f;
}
for(int x=g-1;x>=0;x--){
if(c[x]>=10)printf("%c",c[x]+'A'-10);
else printf("%d",c[x]);
}
基础算法
史蒂夫的农场(模拟)
题目链接:D-史蒂夫的农场_一石月赛(第八期) (nowcoder.com)
补:注意题目的意思是没有必须左右相邻的树判断高度,所以例如1 0 0 0 0 0 1的结果 应是5
代码:
#include
using namespace std;
const int N=1e5+10;
int nums[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
//int* nums = new int [n];
int mai = 0;
for (int i = 0; i < n; i++) {
cin >> nums[i];
if (nums[i] > nums[mai])
mai = i;
}
long long sum = 0;
for (int i = 0, si = i; i < mai; i++) {
if (nums[i] > nums[si])
si = i;
else sum += nums[si] - nums[i];
}
for (int i = n - 1, si = i; i > mai; i--) {
if (nums[i] > nums[si])
si = i;
else sum += nums[si] - nums[i];
}
cout << sum;
} 做题感想:
关于需要模拟的题就是阅读理解,要是理解错误,还不如一开始就不写,从一开始出发的方向都是错的。
怀疑自己是毒药。永远不要怀疑自己。不要给自己怀疑自己的机会。我信奉条理,只要按照一定的条理就会接近目的,达成目的。自己按照条理,就没有什么是自己的问题。
这题做不出来我还差点怀疑自己最近脑子玩坏了,结果其实就是题的问题。不是我的问题。
P1042 乒乓球(模拟)
链接:P1042 [NOIP2003 普及组] 乒乓球 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
#include
using namespace std;
int win[62503];
int w,l;
int main()
{
char s;
for(int i=1;cin>>s&&s!='E';i++)//循环读入,当读到字符E结束
{
if(s=='W')win[i]=1;
else win[i]=2;
}
//----------------11分制 ----------------
for(int i=1;1;i++)
{
if(win[i]==1)w++;//胜场+1
if(win[i]==2)l++;//负场+1
if(win[i]==0)//读到0则记录结束,输出记录结束前的分数。
{
cout<=2||l-w>=2)
if(w>=11||l>=11)//当双方比分相差大于2且一方分数大等于11输出
{
cout<=2||l-w>=2)
if(w>=21||l>=21)//11变为21
{
cout< 榫卯结构(模拟)
链接:B-榫卯结构_重庆移通学院第七届大学生程序设计大赛 (nowcoder.com)
代码:
#include
using namespace std;
int main()
{
int n; cin >> n;
string s[n][3];
for (int i = 0; i < 3; i++) {
for (int j = 0; j < n; j++) {
cin >> s[j][i];
}
}
int a[8]; memset(a, 0, sizeof(a));
for (int i = 0; i < n; i++) {
// 第一对
if (s[i][0] == ".#.") a[0]++;
if (s[i][2] == "#.#") a[4]++;
// 第二对
if (s[i][0][2] == '.' && s[i][2][2] == '.') a[1]++;
if (s[i][1][0] == '.') a[5]++;
// 第三对
if (s[i][2] == ".#.") a[2]++;
if (s[i][0] == "#.#") a[6]++;
// 第四对
if (s[i][0][0] == '.' && s[i][2][0] == '.') a[3]++;
if (s[i][1][2] == '.') a[7]++;
}
if (a[0] == a[4] && a[1] == a[5] && a[2] == a[6] && a[3] == a[7]) {
cout << "Yes";
} else {
cout << "No";
}
return 0;
}
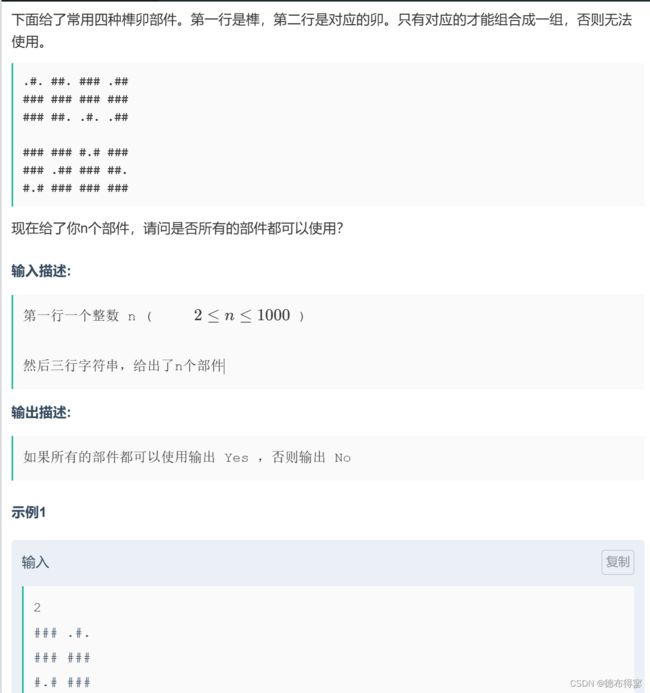
这个题就是被卡输入了我当时比赛的时候。我的思路是没有问题的。
输入应该这样理解:只输入三行,一行有n个小字符串。(n就是总共有多少个部件)
然后这个代码我学习了还可以这样定义string数组 string s[n][3]; 这样就是一个数组内的类型就是一个字符串。然后还可以开的是二维,最后再用三维表示某个点的具体位置
比如这个s[i][0][2] == '.' 意思就是 第i个字符串的第1行(0+1)的第3(2+1)个此处的字符(注意是字符)是‘.’
后面的三维s都是这样理解。
也有教训:好好读题。尤其是疑惑的时候,再多认真读读题,一是冷静下来,二是看遗漏了什么
P267 扫雷游戏(模拟)
链接:P2670 [NOIP2015 普及组] 扫雷游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
using namespace std;
char a[105][105];
int b[105][105],n,m,i,j;//数组定义(二维)
int main()
{
cin>>n>>m;//读入行、列
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cin>>a[i][j];
if(a[i][j]=='*')//判断:如果是地雷
{
b[i+1][j+1]++;
b[i+1][j-1]++;
b[i+1][j]++;
b[i][j+1]++;
b[i][j-1]++;
b[i-1][j]++;
b[i-1][j+1]++;
b[i-1][j-1]++;//相邻的八个格子都+1
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if(a[i][j]=='*')
cout<<"*";//如果是地雷(*) 原样输出
else
cout< 这题居然神奇的不用防止数组越界。可能是+1-1 本来就比较小,而且是从i==1,j==1开始遍历的。
136. 只出现一次的数字(位运算)
问题描述:给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
思路与理解:要对位运算有一个高度的理解,不然还是用哈希表和其他方式解决好理解一些。
class Solution {
public:
int singleNumber(vector& nums) {
int res = 0;
for(int num : nums) res ^= num;
return res;
}
};
注意:这个方法只能处理2个相同的数。处理3个相同的数,找出2个个数为1的数又要另外写代码了。
1024节快乐!(位运算)
问题描述:给你一个16进制数,转换成10进制,然后对1024取模
代码:
#include
#include
using namespace std;
long long int f(string m)
{
long long int res=0,x=0;
int size=m.size();
for(int i = size - 1; res <= 1024 && i >= 0; i--)
{
//模1024 这里必须写res <= 1024 && i >= 0
//当 dec 大于 1024时 直接 % 1024 即可
//<< 4 等价于 * 16
if(m[i]>='0'&&m[i]<='9'){
res = res + ((m[i] - '0') << x);
}else if(m[i]>='A'&&m[i]<='Z'){
res = res + ((m[i] - 'A' + 10) << x);
}else{
res = res + ((m[i] - 'a' + 10) << x);
}
x += 4;
}
return res%1024;
}
int main ()
{
string n;
cin >>n;
cout< P1469 找筷子(位运算)
链接:P1469 找筷子 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
理解:其实和136.只出现一次的数一个原理
代码(自己写的):
#include
using namespace std;
const int N=1e7+5;
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
long long int n,a,res=0;
cin >>n;
for (int i=0;i>a;
res^=a;
}
cout < P1100 高低位交换(位运算)
链接:P1100 高低位交换 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
using namespace std;
int main(){
unsigned int n;
cin>>n;
cout<<(n>>16)+(n<<16);
return 0;
} 学习了:
789. 数的范围(二分)
题目链接:789. 数的范围 - AcWing题库
题解:这里需要二分出数的始末位置,所以要写两个二分来找到始位置和末位置。
找开始的位置二分写法和找末尾的位置的写法不同。需要注意
代码:
#include
using namespace std;
const int N = 100010;
int n, m;
int q[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
while (m -- )
{
int x;
scanf("%d", &x);
int l = 0, r = n - 1;
while (l < r) //找到最后l==r ,跳出循环
{
int mid = l + r >> 1;
if (q[mid] >= x) r = mid; //找始位置
else l = mid + 1;
}
if (q[l] != x) cout << "-1 -1" << endl;
else
{
cout << l << ' ';
int l = 0, r = n - 1;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (q[mid] <= x) l = mid; //找末位置
else r = mid - 1;
}
cout << l << endl;
}
}
return 0;
}
P2249 查找(二分)
链接:P2249 【深基13.例1】查找 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:二分,实际和 789. 数的范围(二分)这个题是一样,找出左边出现的第一个
代码:
#include
using namespace std;
const int N=1e6+10;
int a[N];
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
long long int n,m;
cin >>n>>m;
for (long long int i=0;i>a[i];
}
while (m--)
{
long long int fd ;
cin >>fd ;
long long int l=0,r=n-1;
while (l> 1;
if (a[mid]>=fd) r=mid;
else l=mid+1;
}
if (a[l]!=fd) cout <<"-1"<<' ';
else cout < P7072 直播获奖(排序)(桶排序优化)
题目链接:P7072 [CSP-J2020] 直播获奖 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
1.暴力:直接模拟,把数放在一个数组里面,然后循环输出每次现有数的前百分之w个数的最后一个。
代码:
#include
#include
using namespace std;
const int N=1e5+10;
int a[N];
int n,w,now;
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
cin >> n>>W;
for (int p = 1; p <= n; p++)
{
now=max(1,p*w/100);
//必须要写成max(1, );这种形式因为这里有个细节,p*w/100会出现小于1的情况,没法向上取整
cin >>a[p];
sort(a+1, a+p+1, greater());
cout <>' '
}
return 0;
} 虽然时间复杂度是n但是由于n值过大而且每次sort排序都会消耗很多时间还是过不了全部:
2.桶排序
桶排序思想:
待排序的值在一个明显的整型范围内可以用桶排序来解决。
可以设定有限个序桶(整型数组)把待排序的值装入桶中。
就比如说待排序的数值中有一个数是1,那么我们就要把数字1装在序号是1的桶中(数组a[1]),
桶的序号就是待排序数值的值,而相同的数的个数则包含在数组a[i]。
代码:
#include
using namespace std;
int t[605];
int n,w;
int main()
{
int x;
cin>>n>>w;
for(int i=1;i<=n;i++)
{
cin>>x;
t[x]++;
int sum=0;
for(int j=600;j>=0;j--)
{
sum+=t[j];
if(sum>=max(1,i*w/100))
{
cout< 区间-2(排序)(桶排序优化)
链接:登录—专业IT笔试面试备考平台_牛客网
1.直接模拟(暴力)
会有STL
#include
using namespace std;
const int N=1e5+10;
int a[N];
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int n,m,res=0;
cin >>n>>m;
for (int i=0;i>a[i];
}
while(m--)
{
int l,r;
cin >>l>>r;
for (int i=0;i 2.优化暴力,对数据排序,进而使用桶排序思路
#include
using namespace std;
const int Max = 1000001;
int nums[Max]={0},k[Max]= {0};
int main(){
int n,m;
long long count = 0;
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++){
cin >> nums[i];
k[nums[i]]++; //桶排序 1 把待排序的数放进桶里(相同的数放在同一个桶里)
}
for(int i = 1;i < Max;i++){
k[i]+=k[i-1]; // 2.记录总个数
}
while(m--){
int l,r;
cin >> l >> r;
count += k[r] - k[l-1];
}
printf("%ld",count);
return 0;
} P1271 选举学生会(排序)
链接:P1271 【深基9.例1】选举学生会 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路:直接sort
代码:
#include
using namespace std;
const int N=2000000+5;
int a[N];
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int n,m;
cin >>n>>m;
for (int i=0;i>a[i];
}
sort(a,a+m);
for (int i=0;i (此题十分水,图一乐)
(sort 待深入 ,记忆 )
P1059 明明的随机数(排序)(set·STL)
描述:给一串数字,里面有重复的数,输出从小到大排序的数,并且没有重复的数
代码(自己):
#include
using namespace std;
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
set a;
int n,m;
cin >>n;
for (int i=0;i>m;
a.insert(m);
}
cout < set的插入,遍历,以及set的自动排序(从小到大)
P8218 求区间和(前缀和)
链接:P8218 【深进1.例1】求区间和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
using namespace std;
const int N=1E5+10;
int a[N];
int s[N];
int main ()
{
int n;
cin >>n;
for (int i=1;i<=n;i++)
{
cin >>a[i];
s[i]=s[i-1]+a[i];
}
int m;
cin>>m;
while (m--)
{
int a,b;
cin >>a>>b;
cout < 1530. 最短距离(前缀和)(环处理)
1530. 最短距离 - AcWing题库
代码:
#include
using namespace std;
const int N = 2e5 + 10;
int n, m, s[N];
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++) cin >> s[i], s[i + n] = s[i];
for (int i = 1; i <= n + n; i ++) s[i] += s[i - 1];
cin >> m;
while (m --)
{
int a, b;
cin >> a >> b;
if (a > b) swap(a, b);
cout << min(s[b - 1] - s[a - 1], s[a + n - 1] - s[b - 1]) << endl;
}
}
学习了:
1.环处理,把环型的数组数据拆开,开2倍的空间 s[i + n] = s[i];
七夕礼物(前缀和)(双指针)
题目链接:https://www.lanqiao.cn/problems/1373/learning/
(此题描述有问题)补充:必须是连续的购买礼物。
思路与理解:
用前缀和把所有连续区间的数组数联系起来。用双指针(双指针顾名思义就是用两个左右的指针,具体的代码要根据逻辑来,没有定式)维护连续的区间,满足题目条件。
注意:
(???前缀和排序??? 后面再看看 ,我一次我还没注意,现在看到了反而我不理解了)
代码:
#include
#include
using namespace std;
const int N = 1e5 + 10;
int s[N];
int main() {
int n, t;
cin >> n >> t;
int ans = t;
for (int i = 1; i <= n; i++) {
cin >> s[i];
s[i] += s[i - 1];
}
sort(s, s + n + 1);
int i = 0, j = 1, sum;
while (j <= n) {
sum = s[j] - s[i];
ans = min(ans, abs(t - sum));
if (sum > t) {
i++;
if (i == j) {
j++;
}
}
else if (sum < t) {
j++;
}
else {
ans = 0;
break;
}
}
cout << ans << endl;
return 0;
} 锻造兵器(哈希表STL)
题目链接:锻造兵器 - 蓝桥云课 (lanqiao.cn)
问题描述:给一串数,其中每个数与其他数两两相减得一个定值c,说明两个数是一个定值。求有多少对这种数。
思路与理解:
使用STL的#include
用unordered_map
做题感悟:对题目意思的解读往往可以从同一个词翻译成另一个词,但是含义是不变的。比如这个题,要求差值为c的数的个数,翻译成另一个词就是间隔数是c的数的个数,用“间隔”这个词就可以联想到哈希unordered_map
unordered_map基础知识:
代码:
#include
#include
using namespace std;
const int N=2*1e5+10;
int a[N];
int main()
{
int n,m;
cin>>n>>m;
unordered_map q;
for(int i=1;i<=n;i++)
{
cin>>a[i];
q[a[i]]++;
}
long long ans=0;
for(int i=1;i<=n;i++)
{
ans+=q[a[i]+m];
}
cout< 560. 和为 K 的子数组(前缀和)(哈希表STL)
问题描述:
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
子数组是数组中元素的连续非空序列。
思路与理解:
1.前缀和(n^2)(有点暴力)
直接得出数组的每组数的和。
代码:
class Solution {
public:
int subarraySum(vector& nums, int k) {
int len = nums.size();
// 计算前缀和数组
vector preSum(len + 1, 0);
for (int i = 0; i < len; i++) {
preSum[i + 1] = preSum[i] + nums[i];
}
int count = 0;
for (int left = 0; left < len; left++) {
for (int right = left; right < len; right++) {
// 区间和 [left..right],注意下标偏移
if (preSum[right + 1] - preSum[left] == k) {
count++;
}
}
}
return count;
}
}; //n^2 但是cpp力扣还是不给过 代码是正确的 java同样的代码给过
2.前缀和+ unordered_map
得出公式
这样就用 unordered_map 记录pre[i]-k出现的次数就可以了
代码:
class Solution {
public:
int subarraySum(vector& nums, int k) {
int preSum = 0; // 前缀和
int ans = 0; // 最后答案
unordered_map mp;
mp[0] = 1; // mp初始化
for(int num : nums){
preSum += num; // 遍历到当前数字的前缀和preSum[j]
if(mp.count(preSum - k)){ // 判断preSum[i-1] = preSum[j] - k是否存在
ans += mp[preSum - k]; // 有几个区间前缀和等于preSum-k的区间,答案就加上几
}
mp[preSum] ++; // 前缀和为preSum的区间个数+1
}
return ans;
}
};
//其实大概思路理解了,但是map代码具体就是这样写一个都不能改,我也不知道为什么。就这样记吧
//后面在遇到需要用unordered_map再总结吧 做题感悟:
如果想暴力解决题的话至少时间复杂度是n^2。
在得出解决题目的公式的时候是很有用的,得出计算的公式直接把公式用在代码上可以使代码非常简洁或者时间复杂度也可以降低一个档次。
717. 简单斐波那契(递推)
代码:
#include
using namespace std;
int fb[50];
int main()
{
int n;
cin>>n;
fb[0] = 1;
cout< P1255 数楼梯(高精度加法)(递推)
链接:记录详情 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
using namespace std;
int n,f[5010][5010],len;
void jiafa(int k)//高精加法
{
for(int i=1; i<=len; i++)//两数相加
f[k][i]=f[k-1][i]+f[k-2][i];
for(int i=1; i<=len; i++)//进位
if(f[k][i]>=10)
{
f[k][i+1]+=f[k][i]/10;
f[k][i]%=10;
if(f[k][len+1]>0)len++;
}
}
int main()
{
cin>>n;
len=1;
f[1][1]=1;//预处理
f[2][1]=2;//预处理
for(int i=3; i<=n; i++)//开始计算
jiafa(i);
for(int i=len; i>=1; i--)//输出
cout< 学习了:
1.新的高精度加法的模版(感觉这个好理解,不过空间复杂度太高了)(下次适用闫式高精度加法)
2.递推思想
本体的递推思路是
P1044 栈(递归)(递推)(DP)
链接:P1044 [NOIP2003 普及组] 栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
描述:给定n,有一个队列,一个栈,输出1到n从队列到栈,最后出栈的数的序列个数
代码:
//记忆化搜索/递归 做法
#include
#define MAX_N 20
#define ll long long
using namespace std;
int n;
ll f[MAX_N][MAX_N];
ll dfs(int i,int j)
{
if(f[i][j]) return f[i][j];
if(i==0)return 1; //边界 (队列里没有数了,就有1种情况)
if(j>0) f[i][j]+=dfs(i,j-1);//栈不空时出栈
f[i][j]+=dfs(i-1,j+1); //栈空时进栈
/*这样就已经写完了所以的情况*/
return f[i][j];
int main()
{
scanf("%d",&n);
printf("%lld",dfs(n,0));
return 0;
}
················································
//递归转递推 递推做法
#include
#define MAX_N 20
#define ll long long
using namespace std;
int n;
ll f[MAX_N][MAX_N];
int main()
{
scanf("%d",&n);
for(int i=0;i<=n;i++)
{
f[0][i]=1; //表示队列里面没有数的时候情况是1(和递归的if(i==0)return 1;一样)
}
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
if(i==j)f[i][j]=f[i-1][j];
//队列里面和出栈的数相同的时候,就是2i,栈里面就是没有数了,所以再进栈
else f[i][j]=f[i][j-1]+f[i-1][j];
}
}
printf("%lld",f[n][n]);
return 0;
} AcWing 95. 费解的开关(递推)(枚举)(位运算)
链接:95. 费解的开关 - AcWing题库
代码:
#include
using namespace std;
const int N=6; //题目中的数据是5X5的二维字符数组,在结尾处有\0
//g[][]用来存储25盏灯的初始状态
char g[N][N],backup[N][N]; //backup[][]用来备份这25盏灯
int dx[5]={-1,0,1,0,0},dy[5]={0,1,0,-1,0}; //执行开关灯操作对应的五个位置
void turn(int x,int y) //执行开关灯操作
{
for(int i=0;i<5;i++) //循环五次
{
int a=x+dx[i],b=y+dy[i]; //新的坐标位置
if(a<0||a>=5||b<0||b>=5) continue; //如果新的坐标位置不在方形内重新开始循环
g[a][b]^=1; //字符1的ASCII码为49,0的ASCII码为48转化为二进制最后一位分别是1,0
} //^表示异或运算 0^1=1,1^1=0
} //通过位运算来优化操作
int main()
{
int q;
cin>>q;
while(q--) //执行q次操作
{
for(int i=0;i<5;i++) cin>>g[i]; //输入25盏灯的状态
int res = 10; //初始化答案,只要大于6即可
for(int op=0;op<32;op++) //第一行一共5个元素可以操作2^5=32次
{ //从一行开始枚举进行操作
memcpy(backup,g,sizeof g); //备份25盏灯
int step=0; //step用来存储操作的次数
for(int i=0;i<5;i++)
{
if(op>>i&1) //右移i位与1相当于表示第一行第5-i个位置
{
step++; //操作步数加1
turn(0,i); //进行操作
}
}
for(int i=0;i<4;i++)
{
for(int j=0;j<5;j++)
{
if(g[i][j]=='0') //如果这个位置的灯是灭的
{
step++; //步骤数加1
turn(i+1,j); //对该位置的下一行进行操作
}
}
}
bool dark=false; //dark变量表示最后一行是否全亮
for(int i=0;i<5;i++)
{
if(g[4][i]=='0') //如果最后一行出现不亮的灯0
{
dark=true; //dark为真
break; //终止循环
}
}
if(!dark) res=min(res,step); //最后一行全都亮表示所有灯都点亮了
memcpy(g,backup,sizeof g); //本次循环结束后将初始状态复原到g数组
}
if(res>6) res=-1; //大于6输出-1
cout< 关键点解释:
(详细见:AcWing 95. 费解的开关(有图超详细,看不懂揍我) - AcWing)
1.op==32
2.turn 函数执行的5个操作:
![]()
字符串
标题统计
代码:
#include
#include
using namespace std;
int main() {
string str;
int cnt = 0;
getline(cin, str); // 读入整行包括空格的字符串
for(char&c:str)
if (c != ' ' && c != '\n')
cnt++;
cout << cnt;
}
三带一 (哈希表STL)
题目链接:三带一【算法赛】 - 蓝桥云课 (lanqiao.cn)
思路与理解:
直接用unordered_map计数
代码:
#include
#include
using namespace std;
int main()
{
int m;
cin >>m;
while (m--)
{
int res=0;
string s1;
unordered_map map;
cin >>s1;
for (int i=0;i<4;i++)
{
map[s1[i]]++;
}
for (auto &it:map)
{
if (it.second==3)
{
cout << "Yes" < 教训:注意NO与No(被坑了半天)
罗马数字(字符串)(哈希表STL)
题目链接:罗马数字 - 蓝桥云课 (lanqiao.cn)
代码:
1.手写(麻烦,模拟)
#include
#include
using namespace std;
const int N=105;
int s[N];
int f(string a)
{
int n=a.size(),I=0,cnt=0,res=0,max=0;
for (int i=0;i=max) max =s[i],I=i;
}
for (int i=0;i>n;
while (n--)
{
string s;
cin >>s;
cout < 2.哈希表(方便)
#include
using namespace std;
int n;
string s;
map mp;
int main(){
mp['I']=1,mp['V']=5,mp['X']=10,mp['L']=50,mp['C']=100,mp['D']=500,mp['M']=1000;
cin>>n;
while(n--){
cin>>s;
int len=s.size();
int k=mp[s[len-1]];
for(int i=len-1;i>0;i--){
if(mp[s[i]]>mp[s[i-1]]) k-=mp[s[i-1]];
if(mp[s[i]]<=mp[s[i-1]]) k+=mp[s[i-1]];
}
cout< 被替换的身份证(模拟)(哈希表STL)
链接:被替换的身份证【算法赛】 - 蓝桥云课 (lanqiao.cn)
思路与理解:用哈希表存char转成int 的数比较大小。思路十分清晰易懂
代码:
#include
using namespace std;
map mp;
int main()
{
mp['3']=3,mp['4']=4,mp['5']=5,mp['6']=6,mp['7']=7,mp['8']=8,mp['9']=9,mp['X']=10,mp['J']=11,mp['Q']=12,mp['K']=13,mp['A']=14,mp['2']=15,mp['M']=99,mp['F']=999;
int m;
cin >>m;
while (m--)
{
string a,b;
cin >>a >>b;
if (mp[a[0]]-mp[a[1]]==0||abs(mp[a[0]]-mp[a[1]])==900) cout <<"ShallowDream"< (以后要是自己做的题,代码是自己写的我就把思路与理解写在代码的前面。要是是学习的别人的代码我就把理解思路与学到写在代码的后面)
删除字符(贪心)
删除字符 - 蓝桥云课 (lanqiao.cn)
(此题给的数据过于过,只有一个测试数据,不过不用管,自己的代码写对能过所以情况就行)
问题描述:
代码(包含理解与分析):
#include
#include
using namespace std;
int main ()
{
string s;
char max;
cin >>s;
int n,si=-1;
cin >>n;
int m=s.size()-n;
//贪心,每次找最小的那个输出
for (int j=m;j>0;j--)
{
++si;
max='Z';
for (int i = si;i 做题有感:
做算法题,编程题,要充分分析题目给的逻辑与条件并且加以使用为了解题。
敲代码的就是要充分将逻辑体现在代码上。其中的精髓之处要靠慢慢悟。会提升理解。
318. 最大单词长度乘积(位运算)
代码:
class Solution {
public:
int maxProduct(vector& words) {
int length = words.size();
vector masks(length);
for (int i = 0; i < length; i++) {
string word = words[i];
int wordLength = word.size();
for (int j = 0; j < wordLength; j++) {
masks[i] |= 1 << (word[j] - 'a');
}
}
int maxProd = 0;
for (int i = 0; i < length; i++) {
for (int j = i + 1; j < length; j++) {
if ((masks[i] & masks[j]) == 0) {
maxProd = max(maxProd, int(words[i].size() * words[j].size()));
}
}
}
return maxProd;
}
};
学习了:
1. vector
string 型数组,有几组(个)string ,要具体使用里面的字符串要拿出来赋值使用string word = words[i];
2.用位运算求一组字符串里有没有公共字符
masks[i] |= 1 << (word[j] - 'a');
最后比较(masks[i] & masks[j]) == 0 表示没有公共字符
287. 寻找重复数(模拟)(双指针)
问题描述:所有的 0 都在 1 之前 且其中 0 的数量等于 1 的数量,则认为 s 的这个子字符串是平衡子字符串。返回 s 中最长的平衡子字符串长度。
代码:
双指针解法:
class Solution {
public:
int findTheLongestBalancedSubstring(string s) {
int res=0;
for (int i=1;i=0&&r 学习了(注意):
r-l-1
因为while退出循环前会再执行一次下面的代码,条件不满足while里面的条件才会退出循环。
例如000111,最后返回的是6,这里不是r-l+1(5-0+1),而是r-l-1(6-(-1)-1),因为最后r=5,l=0时,会再执行一次 l--,r++;才跳出循环。
模拟解法:
class Solution {
public:
int findTheLongestBalancedSubstring(string s) {
int n = s.size();
int ans = 0, i = 0;
while (i < n)
{
if (s[i] == '0') {
int j = i + 1;
while (s[j] == '0')
j++;
int k = j;
while (k < n && s[k] == '1' && (k - j + 1) <= (j - i))
k++;
ans = max(ans, 2 * min(k - j, j - i));
i = k;
} else i++;
}
return ans;
}
};遍历一遍字符串 ,从找到0开始执行操作,往后找1,得到ans;以此类推找多个从0开始的组。最后输出最大的。
回文字符串(双指针)
链接:A-回文字符串_重庆移通学院第七届大学生程序设计大赛 (nowcoder.com)
代码:
#include
#include
using namespace std;
int main()
{
string s;
cin >> s;
int l = 0, r = s.size() - 1;
while(l < r)
{
s[l] = s[r] = min(s[l], s[r]);
l++;
r--;
}
cout << s << "\n";
return 0;
} 哎 还是对题目给的意思自己有误解 ,再加上畏惧之前看到过但是没去练过的经典题目“回文串”。
三句话没一句是废话。第一句表示是个回文就行,要操作最少次数,暗示双指针从前和从后。
最后一句要字典序最小不是说整个最小比如babc输出的是abba 而是baab
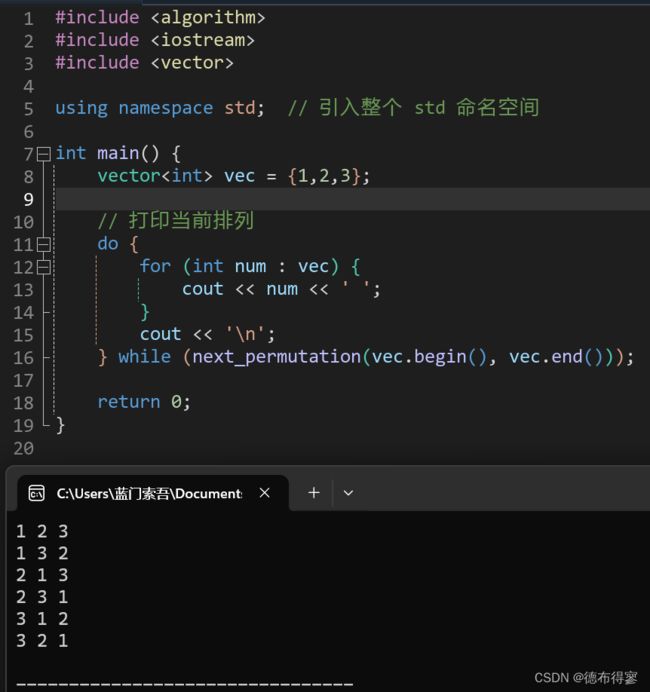
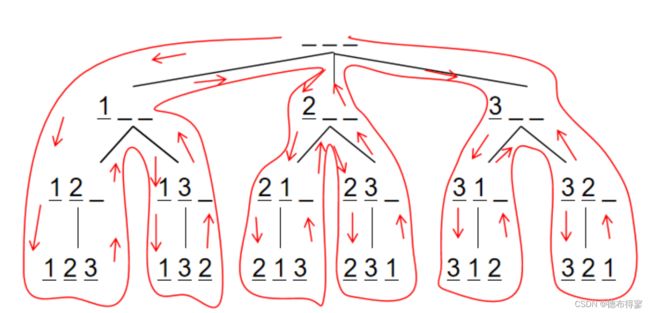
Wrong Word(枚举)(next_permutation)
链接:L-Wrong Word_哈尔滨理工大学软件与微电子学院程序设计竞赛(同步赛) (nowcoder.com)
代码:
#include
using namespace std;
int a[105];
int main(){
string s;
cin >>s;
int len=s.size();
for(int i=0;i 学习了:
1.
next_permutation
全排列函数,把一个从小到大的一段数组全排列。
用法示例
数据结构
P4913 二叉树深度 (二叉树)
链接:【数据结构1-2】二叉树 - 题单 - 洛谷
代码:
#include
#define _for(i, a, b) for (int i=(a); i<=(b); i++)
using namespace std;
const int MAXN = 1e6 + 10;
struct node {
int left, right;
};
node tree[MAXN];//存储结构定义
int n, ans;
void dfs(int id, int deep) {
if (id == 0) return ;//到达叶子节点时返回
ans = max(ans, deep);//更新答案
dfs(tree[id].left, deep+1);//向左遍历
dfs(tree[id].right, deep+1);//向右遍历
}
int main() {
cin >> n;
_for (i, 1, n) cin >> tree[i].left >> tree[i].right;//读入+建树
dfs(1, 1);//从1号节点出发,当前深度为1
cout << ans << endl;//输出答案
return 0;//完结撒花!
}
注意:根节点描述固定为1.
第 i行两个整数 l、r,分别表示结点 i的左右子结点编号
P4715 淘汰赛(queue_STL)(pair_STL)
链接:P4715 【深基16.例1】淘汰赛 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
#include
#include P1416 攻击火星(模拟)(图)
题目链接:P1416 攻击火星 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
问题描述:构造一个无向图有n个点,使得从度为0到n-1的点开始删除后剩下的点要最多。
思路与理解:
代码:
#include
using namespace std;
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int n;
cin >>n;
cout < 做题感想:这种模拟,需要自己构造现想的题,就是要靠刷题积累经验,遇到过就会,没遇到过就不会。
AcWing 154. 滑动窗口 (单调队列)
问题描述:
有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k个数字。
每次滑动窗口向右移动一个位置。
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
思路与理解:
作为模版题没有什么多说的,具体有的时候想不起来理解的时候可以看这个题解AcWing 154. 滑动窗口 - AcWing
和这个视频讲解都讲的很好411【模板】单调队列 滑动窗口最值_哔哩哔哩_bilibili
代码:
# include
using namespace std;
const int N = 1000010;
int a[N], q[N], hh, tt = -1;
int main()
{
int n, k;
cin >> n >> k;
for (int i = 0; i < n; ++ i)
{
scanf("%d", &a[i]);
if (i - k + 1 > q[hh]) ++ hh; // 若队首出窗口,hh加1
while (hh <= tt && a[i] <= a[q[tt]]) -- tt; // 若队尾不单调,tt减1
//构造单调递增队列
//当队列不为空(hh <= tt) 且 当队列队尾元素>=当前元素(a[i])时,那么队尾元素
//就一定不是当前窗口最小值,删去队尾元素,加入当前元素(q[ ++ tt] = i)
q[++ tt] = i; // 下标加到队尾
if (i + 1 >= k) printf("%d ", a[q[hh]]); // 输出结果
}
cout << endl;
hh = 0; tt = -1; // 重置!
for (int i = 0; i < n; ++ i)
{
if (i - k + 1 > q[hh]) ++ hh;
while (hh <= tt && a[i] >= a[q[tt]]) -- tt;
q[++ tt] = i;
if (i + 1 >= k) printf("%d ", a[q[hh]]);
}
return 0;
}
P2629 好消息,坏消息(前缀和)(单调队列)
(预计明天更新做题的题解)
11111
1111
111
835. Trie字符串统计 (Trie)(模版题)
题目链接:835. Trie字符串统计 - AcWing题库
问题描述:
维护一个字符串集合,支持两种操作:
I x向集合中插入一个字符串 x;Q x询问一个字符串在集合中出现了多少次。
思路与理解:直接背模版就好。理解部分大概。
代码:
//Trie树快速存储字符集合和快速查询字符集合
#include
using namespace std;
const int N = 100010;
//son[][]存储子节点的位置,分支最多26条;
//cnt[]存储以某节点结尾的字符串个数(同时也起标记作用)
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][26], cnt[N], idx;
char str[N];
void insert(char *str)
{
int p = 0; //类似指针,指向当前节点
for(int i = 0; str[i]; i++)
{
int u = str[i] - 'a'; //将字母转化为数字
if(!son[p][u]) son[p][u] = ++idx; //该节点不存在,创建节点
p = son[p][u]; //使“p指针”指向下一个节点
}
cnt[p]++; //结束时的标记,也是记录以此节点结束的字符串个数
}
int query(char *str)
{
int p = 0;
for(int i = 0; str[i]; i++)
{
int u = str[i] - 'a';
if(!son[p][u]) return 0; //该节点不存在,即该字符串不存在
p = son[p][u];
}
return cnt[p]; //返回字符串出现的次数
}
int main()
{
int m;
cin >> m;
while(m--)
{
char op[2];
scanf("%s%s", op, str);
if(*op == 'I') insert(str);
else printf("%d\n", query(str));
}
return 0;
}
836. 合并集合(并查集)
题目链接:836. 合并集合 - AcWing题库
问题描述:
代码:
#include
using namespace std;
const int N = 100010;
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) p[i] = i;
while (m -- )
{
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if (*op == 'M') p[find(a)] = find(b);
else
{
if (find(a) == find(b)) puts("Yes");
else puts("No");
}
}
return 0;
}
837. 连通块中点的数量(并查集)
问题链接:https://www.acwing.com/problem/content/839/
问题描述:
代码:
#include
using namespace std;
const int N = 100010;
int n, m;
int p[N], cnt[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
cnt[i] = 1;
}
while (m -- )
{
string op;
int a, b;
cin >> op;
if (op == "C")
{
cin >> a >> b;
a = find(a), b = find(b); //先把a,b的根结点取出来
if (a != b)
{
p[a] = b;// 集合a接到集合b下
cnt[b] += cnt[a];
}
}
else if (op == "Q1")
{
cin >> a >> b;
if (find(a) == find(b)) puts("Yes");
else puts("No");
}
else
{
cin >> a;
cout << cnt[find(a)] << endl;
}
}
return 0;
}
1249. 亲戚(并查集)
题目链接:1249. 亲戚 - AcWing题库
问题描述:本质就是无向图,用并查集的板子就可以做
代码:
#include
using namespace std;
const int N = 20010;
int p[N];
int find (int x)
{
if (p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
int n,m;
cin >>n>>m;
for (int i = 1; i <= n; i ++ )
{
p[i]=i;
}
while (m -- )
{
int a,b;
cin >>a>>b;
a=find(a),b=find(b);
p[a]=b;
}
int q;
cin >>q;
while(q--)
{
int a,b;
cin >>a>>b;
if (find(a)==find(b)) puts("Yes");
else puts("No");
}
return 0;
} 注意:
1.cin cout 会超时 取消同步流加速输入输出
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
2.cout输出会慢一些,用puts或printf会快些防止超时
换行使用'\n'会比endl;快
AcWing 840. 模拟散列表(哈希表)
问题描述:
思路与理解:
拉链法
代码:
#include
#include
using namespace std;
const int N = 100003; //取大于1e5的第一个质数,取质数冲突的概率最小
//* 开一个槽 h
int h[N], e[N], ne[N], idx; //单链表
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ; //头插法
}
bool find(int x)
{
int k = (x % N + N) % N; //c++中如果是负数那他取模也是负的所以 加N 再 %N 就一定是一个正数
//Hash函数 讲x映射到 从 0-1e5 之间的数
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
int main()
{
int n;
scanf("%d", &n);
memset(h, -1, sizeof h) //将槽先清空 空指针一般用 -1 来表示
while (n -- )
{
char op[2];
int x;
scanf("%s%d", op, &x);
if (*op == 'I') insert(x);
else
{
if (find(x)) puts("Yes");
else puts("No");
}
}
return 0;
}
AcWing 848. 有向图的拓扑序列(拓扑排序)
链接:https://www.acwing.com/problem/content/850/
代码:
#include
#include
#include
using namespace std;
const int N = 100010;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int q[N], hh = 0, tt = -1;//队列保存入度为0的点,也就是能够输出的点,
int n, m;//保存图的点数和边数
int d[N];保存各个点的入度
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void topsort(){
for(int i = 1; i <= n; i++){//遍历一遍顶点的入度。
if(d[i] == 0)//如果入度为 0, 则可以入队列
q[++tt] = i;
}
while(tt >= hh){//循环处理队列中点的
int a = q[hh++];
for(int i = h[a]; i != -1; i = ne[i]){//循环删除 a 发出的边
int b = e[i];//a 有一条边指向b
d[b]--;//删除边后,b的入度减1
if(d[b] == 0)//如果b的入度减为 0,则 b 可以输出,入队列
q[++tt] = b;
}
}
if(tt == n - 1){//如果队列中的点的个数与图中点的个数相同,则可以进行拓扑排序
for(int i = 0; i < n; i++){//队列中保存了所有入度为0的点,依次输出
cout << q[i] << " ";
}
}
else//如果队列中的点的个数与图中点的个数不相同,则可以进行拓扑排序
cout << -1;//输出-1,代表错误
}
int main(){
cin >> n >> m;//保存点的个数和边的个数
memset(h, -1, sizeof h);//初始化邻接矩阵
while (m -- ){//依次读入边
int a, b;
cin >> a >> b;
d[b]++;//顶点b的入度+1
add(a, b);//添加到邻接矩阵
}
topsort();//进行拓扑排序
return 0;
}
P4017 最大食物链计数(拓扑排序)
链接:P4017 最大食物链计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
1.用邻接矩阵存图,使用stl自带的队列
#include
using namespace std;
int n,m,ru[5005],chu[5005],a,b,f[5005],ans;
int mp[5005][5005];
queue q;
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
scanf("%d%d", &a, &b);
mp[a][b]=1;//记录关系
chu[a]++;
ru[b]++;//记录入度和出度
}
for(int i=1;i<=n;i++){
if(ru[i]==0) {
f[i]=1;
q.push(i);//入度为零的入队
}
}
while(!q.empty()){//队列不为空
int a=q.front();
q.pop();//出队
for(int k=1;k<=n;k++){
if(mp[a][k]==0)continue;
f[k]+=f[a];//更新
f[k]%=80112002;
ru[k]--;//食物少了一个
if(ru[k]==0){//入队为零才入队
if(chu[k]==0){
ans+=f[k];
ans%=80112002;
continue;//有没有都行
}
q.push(k);
}
}
}
cout< 2.用邻接表存图,使用stl自带的队列
#include
using namespace std;
const int mod=80112002;
int n, m, h[5005], ru[5005], chu[5005], f[5005], ans;
struct AB{
int a,b,n;
}d[5000005];
queue q;
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int a, b;
scanf("%d%d", &a, &b);
d[i].a=a, d[i].b=b, d[i].n=h[a], h[a]=i;//建图
chu[a]++, ru[b]++;
}
for(int i=1;i<=n;i++){
if(ru[i]==0) {
f[i]=1;
q.push(i);
}
}
while(!q.empty()){
int a=q.front();
q.pop();
for(int k=h[a];k;k=d[k].n){
int b=d[k].b;
f[b]+=f[a];
f[b]%=mod;
ru[b]--;
if(ru[b]==0){
if(chu[b]==0){
ans+=f[b];
ans%=mod;
}//出度为0的点为食物链终点,记录答案,并且不必入队
else q.push(b);
}
}
}
cout< 3.使用闫式领接表存图,然后使用数组模拟队列(待更新)
(待)(待提升的深度)学习了:图的储存,队列操作 ,完成拓扑排序。
搜索(BFS,DFS)
842. 排列数字(DFS)
题目链接:
理解与思路:
dfs关键的理解在于一直递归dfs下去向下搜索(要在脑子里知道流程大概是怎么样的)。还有就是回溯。
dfs(u + 1);//填下一个位 这里递归u+1 一直向下 会在深处进行到if (u>n)的判断,不满足时候就会输出。
state[i] = 0;//回溯,取出 i 回溯这里在dfs(u + 1);下面 ,因为一直递归到深处的时候就会从下到上返回,返回后要更新所以的数都没有用过,在下一个左右孩子继续向下搜索的时候用。
根据这道题的代码具体理解
代码:
#include
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)
{
if(u > n)//数字填完了,输出
{
for(int i = 1; i <= n; i++)//输出方案
cout << path[i] << " ";
cout << endl;
}
for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n
{
if(!state[i])//如果数字 i 没有被用过
{
path[u] = i;//放入空位
state[i] = 1;//数字被用,修改状态
dfs(u + 1);//填下一个位
state[i] = 0;//回溯,取出 i
}
}
}
int main()
{
cin >> n;
dfs(1);
}
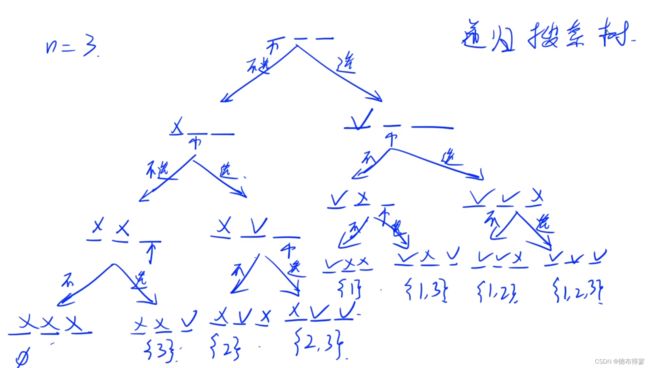
递归实现指数型枚举(DFS)
链接:92. 递归实现指数型枚举 - AcWing题库
代码1:
#include
using namespace std;
const int N=20;
int n;
bool vis[N]; //判断选还是不选
void DFS(int u) //第几层就是筛选第几个数字
{
if(u>n) //不可以有等号,如果有等号会少一层递归,即最后一层无法递归
{
for(int i=1;i<=n;i++)//从1到n选择
if(vis[i]) //把选择的数打印出来
cout<>n;
DFS(1); //从1开始选择,到n结束,所以不能从0开始;
return 0;
}
代码2:
#include
#include
#include
#include
using namespace std;
const int N = 16;
int n;
int st[N]; // 状态,记录每个位置当前的状态:0表示还没考虑,1表示选它,2表示不选它
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i ++ )
if (st[i] == 1)
printf("%d ", i);
printf("\n");
return;
}
st[u] = 2;
dfs(u + 1); // 第一个分支:不选
st[u] = 0; // 恢复现场
st[u] = 1;
dfs(u + 1); // 第二个分支:选
st[u] = 0;
}
int main()
{
cin >> n;
dfs(1);
return 0;
}
题解:
P2196 挖地雷(DFS)
链接:P2196 [NOIP1996 提高组] 挖地雷 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
using namespace std;
bool f[21][21];//记录是否有路径相连
int a[21];//记录地雷数
int path[21],ans[21],cnt;//path记录路径,ans记录答案,cnt记录走了多少个点
bool b[21];//记录该点是否走过
int n;
int maxx;//记录挖的最大地雷数
bool chck(int x)//检查是否还能继续往下挖
{
for(int i=1;i<=n;i++)
{
if(f[x][i]&&!b[i]) return false;
}
return true; /*f[x][i]=0*/
}
void dfs(int x,int stp,int sum)//x记录现在位置,stp记录走了几个点,sum记录挖的地雷数
{
if(chck(x))
{
if(maxx>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i>f[i][j];
}
for(int i=1;i<=n;i++)
{
b[i]=1; /* 1为走过 */
path[1]=i;//记录起点
dfs(i,1,a[i]);
b[i]=0;
}
for(int i=1;i<=cnt;i++)
cout< 93. 递归实现组合型枚举(DFS)
链接:93. 递归实现组合型枚举 - AcWing题库
代码:
#include
using namespace std;
int n,m;
vector num;
void dfs(int k)
{
//如题解所述
if(num.size() > m || num.size() + (n - k + 1) < m)
return;
//到达枚举边界,输出结果并结束
if(k == n + 1)
{
for(int i = 0;i < num.size();++i)
cout << num[i] << " ";
cout << endl;
return;
}
//选择这个数
num.push_back(k);
dfs(k+1);
//回溯
num.pop_back();
//不选择这个数
dfs(k+1);
}
int main(void)
{
cin >> n >> m;
dfs(1);
return 0;
}
其实只需要把例1的代码稍加修改就可以了。再增加两个情况,一种是动态数组所选择的数已经超过了m个,或者剩余的数凑不够m个,排除这两种情况就是我们所要的答案了。
844. 走迷宫(BFS)
题目链接:https://www.acwing.com/problem/content/846/
问题描述:
思路与理解:见代码
代码:
1.手写队列
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
PII q[N * N];//手写队列
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过
d[0][0] = 0;//表示起点走过了
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左
while(hh <= tt)//队列不空
{
PII t = q[hh ++ ];//取队头元素
/*复习++在后和++在前的区别:在后是先使用值,再给只加1;在前是先使用加1之后的值*/
for(int i = 0; i < 4; i ++ )//枚举4个方向
{
int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过
{
d[x][y] = d[t.first][t.second] + 1;//到起点的距离
q[ ++tt ] = {x, y};//新坐标入队
/*q[ ++tt ] = {x, y};从最开始遍历就可以给pair添加数据,不用觉得pair里面没有数据*/
/*这里必须是++tt不能是tt++,因为就是要直接使用加1之后的值让新的数组入队*/
}
}
}
return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
2.STL实现队列(偏向使用这个,因为c++给我提供了我就要用,还方便对队列进行操作)
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
int n, m;
int g[N][N], d[N][N];
int bfs()
{
queue< pair > q; //定义pair型的队列
q.push({0, 0});
memset(d, -1, sizeof(d));
d[0][0] = 0;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (q.size())//队列不为空
{
PII t = q.front();//取队头元素
q.pop();//出队
for (int i = 0; i < 4; i++)
{
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;//当前点到起点的距离
q.push({x, y});//将新坐标入队
}
}
}
return d[n - 1][m -1];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
STL队列的基础知识:
DP,贪心
人肉优化(DP)
链接:F-人肉优化_重庆移通学院第七届大学生程序设计大赛 (nowcoder.com)
描述:![]()
代码:
#include
using namespace std;
long long dp[36];
int main(){
int x;
cin>>x;
dp[0]=0;
dp[1]=1;
dp[2]=2;
for(int i=3;i<=x;i++){
dp[i]=dp[i-3]+2*dp[i-2]+3*dp[i-1];
}
cout< 自己的理解:感觉有点拓展了dp的思维。把递归变成了dp,有初始化值 dp[0]=0; dp[1]=1; dp[2]=2;
状态转移,从最小的状态一直转移到最大的状态。
官方题解:
数字三角形(线性DP)
题目链接:898. 数字三角形 - AcWing题库
问题:给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
代码:
include
include
include
using namespace std;
int n;
int a[1000][1000];
int main()
{
scanf("%d",&n);
for(int i=0;i=0;i--)
{
for(int j=0;j<=i;j++)//for循环按顺序扫描除最后一排前的所有数
a[i][j]+=max(a[i+1][j],a[i+1][j+1]);
//从左下,右下中选取大的加到现在的位置上
}
cout< 代码的思路解释:从倒数第二排依次向最上层开始执行,更新每一层的数字,这个数字选择的是选择左下角或者右下角的合数最大值。这样遍历到最上层的数的时候就是整体的最大值。
(这个思路让我浅尝动态规划这四个字的深意。结果最优,动态规划。每一步最优?以后也多看看贪心)
P1115 最大子段和(简单DP)
链接:P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
描述:
#include
using namespace std;
int n,a,b,i,ans=-2147483647;
int main(){
cin>>n;
for(i=1;i<=n;i++){
cin>>a;
if(i==1) b=a;
else b=max(a,a+b);
/* 用b 和 ans 使用2个max维护最大区间,避免了只有1个max函数 1 1 1 -1 最后是2的错误答案*/
ans=max(ans,b);
}
cout< P1002 过河卒(DP)
链接:P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
描述:给一个二维数组,从左上角走到右下角有多少种走法?有固定的点事不可以走的。输出总共的走法数。
代码:
#include
using namespace std;
long long a,b,n,m,x[23][23],ma[23][23];
void work(long long x,long long y){
ma[x][y]=1;
ma[x-1][y-2]=1;
ma[x-2][y-1]=1;
ma[x-2][y+1]=1;
ma[x-1][y+2]=1;
ma[x+1][y-2]=1;
ma[x+2][y-1]=1;
ma[x+2][y+1]=1;
ma[x+1][y+2]=1;
}
int main(){
scanf("%lld %lld %lld %lld",&n,&m,&a,&b);
a++;
b++;
n++;
m++;
work(a,b);
x[1][1]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i==1&&j==1)continue;
if(ma[i][j]==0)x[i][j]=x[i-1][j]+x[i][j-1];
}
}
printf("%lld",x[n][m]);
return 0;
} 学习了:
逐渐感受到动态规划的思想和一些方法了。
1.
首先是状态转移方程的得出:
一个格子走到当前位置一定是从左边或者上面走到当前位置的这两种走法。我们要求出走到最后一个格子的走法,所以状态转移方程就出来了
f(i,j)=f(i−1,j)+f(i,j−1)
最后我们会得到f(n,m);
2.初始化:
f一开始是0,所以肯定要给一个初始值初始化 f[1][1]=1,表示1,1这个坐标有1个走法(因为出生地所以肯定是1)
待深入:还有可以优化的地方,滚动数组?变成一维f?
防止数组越界?
a++;
b++;
n++;
m++;
P3842 线段(DP)
代码:
#include
using namespace std;
int n,a[20001][2],f[20001][2];//a[i][0]表示l[i],a[i][1]表示r[i]
int dis(int a,int b)//计算距离
{
return abs(a-b);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d%d",&a[i][0],&a[i][1]);
f[1][0]=dis(a[1][1],1)+dis(a[1][1],a[1][0]);
f[1][1]=dis(a[1][1],1);
for(int i=2;i<=n;i++)//状态转移
{
f[i][0]=min(f[i-1][0]+dis(a[i-1][0],a[i][1])+dis(a[i][1],a[i][0]),f[i-1][1]+dis(a[i-1][1],a[i][1])+dis(a[i][1],a[i][0]))+1;
f[i][1]=min(f[i-1][0]+dis(a[i-1][0],a[i][0])+dis(a[i][0],a[i][1]),f[i-1][1]+dis(a[i-1][1],a[i][0])+dis(a[i][0],a[i][1]))+1;
}
printf("%d",min(f[n][0]+dis(a[n][0],n),f[n][1]+dis(a[n][1],n)));//最后的答案还要加上到(n,n)的距离
} 注意:状态转移从上一行到下一行是需要路数加1的。
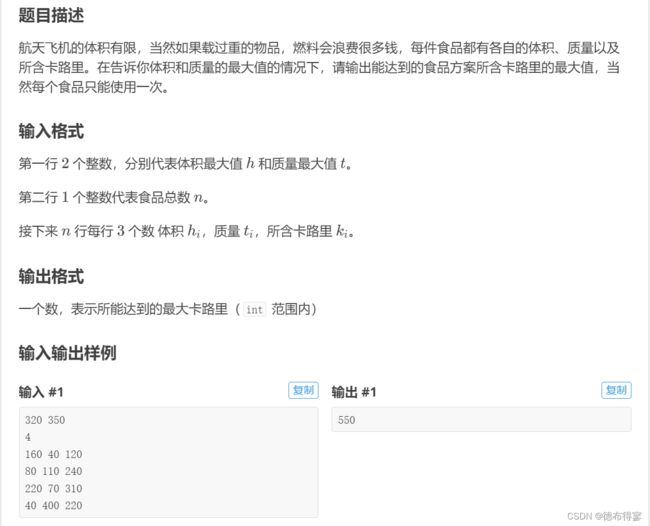
P1507 NASA的食物计划(01背包)
问题描述:
思路:一眼01背包(dp就是要多练,从题中学习)
代码1:最容易理解的,直接开三维数组记录,剩下的套01背包公式
#include
using namespace std;
const int N=600;
int f[N][N][N];
//f[i][j][k] 前i个物品中放入体积为j,质量为k的背包的最优值
int h[N]; //体积
int m[N]; //质量
int w[N]; //卡路里
int main ()
{
cin.tie(0);
ios::sync_with_stdio(false);
int H ,T,n;
cin >>H>>T>>n;
for (int i=1;i<=n;i++)
{
cin >>h[i]>>m[i]>>w[i];
}
for (int i=1;i<=n;i++)
{
for (int j=H;j>0;j--)
{
for (int k=T;k>0;k--)
{
if (j>=h[i]&&k>=m[i])
{
f[i][j][k]=max (f[i-1][j][k],f[i-1][j-h[i]][k-m[i]]+w[i]);
}
else //H>=h[i]&&T>=t[i] 装不下
f[i][j][k]=f[i-1][j][k];
}
}
}
cout << f[n][H][T]< 代码2:降三维为二维不要f[i],因为最后就是要求最后f[n].最外层套for循环的i<=n就达到效果了;
最深层循环的判断直接写在循环的条件里面就行
for (int j=H;j>=h[i];j--)
{
for (int k=T;k>=m[i];k--)
{#include
using namespace std;
const int N=600;
int f[N][N];
//f[i][j][k] 前i个物品中放入体积为j,质量为k的背包的最优值
int h[N]; //体积
int m[N]; //质量
int w[N]; //卡路里
int main ()
{
cin.tie(0);
ios::sync_with_stdio(false);
int H ,T,n;
cin >>H>>T>>n;
for (int i=1;i<=n;i++)
{
cin >>h[i]>>m[i]>>w[i];
}
for (int i=1;i<=n;i++)
{
for (int j=H;j>=h[i];j--)
{
for (int k=T;k>=m[i];k--)
{
f[j][k]=max (f[j][k],f[j-h[i]][k-m[i]]+w[i]);
}
}
}
cout << f[H][T]< P1048 采药(01背包)
代码:
简单的01背包模版
#include
using namespace std;
const int N=105;
int dp[N][1005];
int w[N],val[N];
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int t,m;
cin >>t>>m;
for (int i=1;i<=m;i++)
{
cin >>w[i]>>val[i];
}
for (int i=1;i<=m;i++)
{
for (int j=t;j>=0;j--)
{
if (j>=w[i])
{
dp[i][j]=max(dp[i-1][j-w[i]]+val[i],dp[i-1][j]);
}
else dp[i][j]=dp[i-1][j];
}
}
cout < 被坑:注意数据范围。注意=。脑子热的时候冷静下来,别怀疑自己。
P1802 5 倍经验日(01背包)
链接:P1802 5 倍经验日 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
描述:
代码:
#include
#include
using namespace std;
const int maxn=1006;
long long f[maxn];//一定要用long long!不然只能得90分
long long a[maxn][2];//存赢和输的情况,a[i][0]代表输的,a[i][1]代表赢得
long long b[maxn];
int main(){
int n,x1;
scanf("%d%d",&n,&x1);
long long x,y,z;
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&x,&y,&z);
a[i][0]=x,a[i][1]=y,b[i]=z;
}
for(int i=1;i<=n;i++){
for(int j=x1;j>=0;j--){
if(j>=b[i]){//如果有足够的药剂打赢别人,则看是输好还是赢好
f[j]=max(f[j]+a[i][0],f[j-b[i]]+a[i][1]);
}
else f[j]+=a[i][0];//没有足够药剂就一个都不用直接认输,不然就浪费了药剂
}
}
cout<<5*f[x1];//记得是五倍经验!
} 思路与理解:我也想到了是01背包
本题收获:
1.果然自己只要有思路,不要担心是错的,就是要去写一写,实现不对才看题解。
2.好好读题,获得多的信息,本题就是这样,隐藏的有用信息是每个人都要打1次,打不过不用用药
3.加深了01背包的记忆和理解(或者说是深刻的用法,嘿嘿)
P1049 装箱问题(01背包)
链接:P1049 [NOIP2001 普及组] 装箱问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码(自己写的):
#include
using namespace std;
const int N=20000+5;
int f[N][N],a[N];
int main ()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int v,n;
cin >>v>>n;
for (int i=1;i<=n;i++)
{
cin >>a[i];
}
for (int i=1;i<=n;i++)
{
for (int j=v;j>0;j--)
{
if (j>=a[i])
{
f[i][j]=max(f[i-1][j],f[i-1][j-a[i]]+a[i]);
}
else
{
f[i][j]=f[i-1][j];
}
}
}
cout <<(v-f[n][v])< 一维代码:
#include
using namespace std;
int a[50],dp[20001];
int main() {
int n,m,i,j;
cin>>m>>n;
for(i=0; i>a[i];
for(i=0; i=a[i]; j--)
dp[j]=max(dp[j],a[i]+dp[j-a[i]]);
cout < P1164 小A点菜(01背包)
描述:给出一个固定大小的背包,有多个体积不一的物品,求出装满这个背包的所有情况数
代码:
#include
using namespace std;
const int maxn=10000+10;
int v[maxn],f[maxn];
int main(){
int n,m;
cin>>n>>m;
f[0]=1;
for(int i=1;i<=n;++i)
cin>>v[i];//读入 价值
for(int i=1;i<=n;++i)
for(int j=m;j>=v[i];j--)
f[j]+=f[j-v[i]];//现在的花费+=我不点这个菜的时候的花费
cout< 直接当作01背包的变形:给出一个固定大小的背包,有多个体积不一的物品,求出装满这个背包的所有情况数
公式,直接背。
P1077 摆花(01背包)
链接:P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
描述:给定一个大小为n的背包,这个背包的某一段的种类容量大小固定。输出所有的填满方式个数。
代码1:
#include
using namespace std;
long long b[101][101],n,m,a[101]; //定义数组
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=0;i<=m;i++){b[i][0]=1;} //初始化,不管有多少种花,只要是0盆花,就只有1种可能性,啥都不放
for(int i=1;i<=n;i++)//几种花
for(int j=1;j<=m;j++)//几盆花
for(int k=j;k>=j-a[i];k--)//这种花放多少盆?我们用变量k来循环
{
if(k>=0){b[i][j]+=b[i-1][k]%1000007;b[i][j]%=1000007;}//每次 mod以防万一
else break; //如果超出限制就退出循环
}
cout< 代码2:
#include
using namespace std;
const int maxn=105, mod = 1000007;
int n, m, a[maxn], f[maxn];
int main()
{
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
f[0] = 1;
for(int i=1; i<=n; i++)
for(int j=m; j>=0; j--) //注意,是01背包
for(int k=1; k<=min(a[i], j); k++)
f[j] = (f[j] + f[j-k])%mod;
cout< 理解:这题其实是P1164 小A点菜(01背包)的深入。本质上是一样的。
P1064 金明的预算方案(01背包)
代码:
#include
#define maxn 32005
using namespace std;
int n,m;
int v,p,q;
int main_item_w[maxn];//某个主件的费用
int main_item_c[maxn];//某个主件的价值
int annex_item_w[maxn][3];//某个附件的费用
int annex_item_c[maxn][3];//某个附件的价值
int f[maxn];
int main(){
cin >> n >> m;
for (int i=1;i<=m;i++){
cin >> v >> p >> q;
if (!q){
main_item_w[i] = v;
main_item_c[i] = v * p;
}
else{
annex_item_w[q][0]++; //非常好的存数据方式
annex_item_w[q][annex_item_w[q][0]] = v;
annex_item_c[q][annex_item_w[q][0]] = v * p;
}
}
for (int i=1;i<=m;i++)
for (int j=n;main_item_w[i]!=0 && j>=main_item_w[i];j--){
f[j] = max(f[j],f[j-main_item_w[i]]+main_item_c[i]);
if (j >= main_item_w[i] + annex_item_w[i][1])
f[j] = max(f[j],f[ j - main_item_w[i] - annex_item_w[i][1] ] + main_item_c[i] + annex_item_c[i][1]);
if (j >= main_item_w[i] + annex_item_w[i][2])
f[j] = max(f[j],f[ j - main_item_w[i] - annex_item_w[i][2] ] + main_item_c[i] + annex_item_c[i][2]);
if (j >= main_item_w[i] + annex_item_w[i][1] + annex_item_w[i][2])
f[j] = max(f[j],f[ j - main_item_w[i] - annex_item_w[i][1] - annex_item_w[i][2] ] + main_item_c[i] + annex_item_c[i][1] + annex_item_c[i][2]);
}
cout << f[n] << endl;
return 0;
} 题解:
P1832 A+B Problem(筛质数)(完全背包)
P1832 A+B Problem(再升级) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
问题描述:给定一个正整数 n,求将其分解成若干个素数之和的方案总数。
思路与理解:看一个数n可以由多少个质数组成,质数可以用无数次,求填满背包n的总数,就是完全背包问题。
代码:
#include
using namespace std;
const int N=1005;
int primes[N],cnt=0;
long long dp[N];
bool st[N];
void get_primes(int n)
{
for (int i=2;i<=n;i++)
{
if (st[i]) continue ;
primes[++cnt]=i; // 要写成++cnt 因为后面要用到primes数组是从[1]开始的
for (int j=i+i;j<=n;j+=i)
{
st[j]=true;
}
}
}
int main ()
{
int n;
cin >> n;
get_primes(n);
dp[0]=1;
for (int i=1;i<=cnt;i++)
{
for (int j=primes[i];j<=n;j++)
{
dp[j] += dp[j-primes[i]];
}
}
cout < 代码注意:primes[++cnt]=i; // 要写成++cnt 因为后面要用到primes数组是从[1]开始的
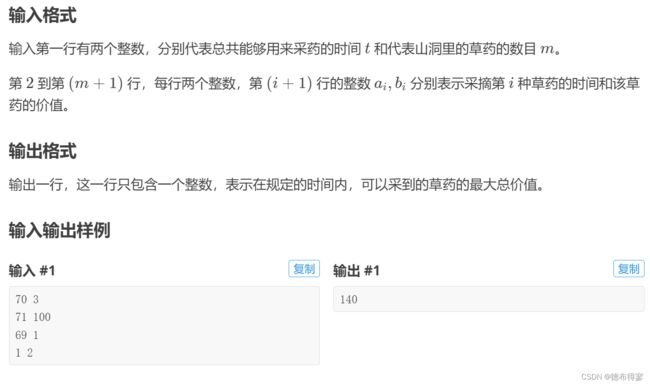
P1616 疯狂的采药(完全背包)
链接:P1616 疯狂的采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
代码:
#include
#define int long long//不开ll见祖宗
using namespace std;
int n,m;
int a[10001];
int b[10001];
int dp[10000001];
signed main(){
cin>>m>>n;
for(int i=1;i<=n;i++)
cin>>a[i]>>b[i];
for(int i=1;i<=n;i++)
for(int j=a[i];j<=m;j++)//必须要有足够的时间采当前草药,所以从a[i]开始循环。
dp[j]=max(dp[j],dp[j-a[i]]+b[i]);
cout< 以后能开一维dp的01或者完全背包就开一维的
901. 滑雪(记忆化搜索)
题目链接:901. 滑雪 - AcWing题库
问题描述:给一个二维数组,每个数表示雪山的高度。滑雪只能从高到低滑行。求这一片雪山(二维数组)最长的滑行距离。
思路与理解:
代码:
#include
#include
#include
using namespace std;
const int N = 310;
int h[N][N];
int n,m;
int f[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1} ; // 上 右 下 左
int dp(int x,int y)
{
int &v=f[x][y]; // 用v代替f[x][y]
if (v!=-1) return v;
v=1;
for (int i = 0; i < 4; i ++ )
{
int a=x+dx[i],b=y+dy[i];
if (a>=1&&a<=n&&b>=1&&b<=m&&h[x][y]>h[a][b])
/*a,b初始>=1因为主函数的双重循环都是从1开始的*/
{
v=max(v,dp(a,b)+1);
/*递归了dp dp(int x,int y),加1表示从坐标(a,b)向下滑的路径总数下加1*/
}
}
return v;
}
int main ()
{
cin >>n>>m;
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
{
cin >> h[i][j];
}
}
memset(f,-1,sizeof f);
int res = 0;
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
{
res = max(res,dp(i,j));
}
}
cout << res < 285. 没有上司的舞会(树形DP)
题目链接:285. 没有上司的舞会 - AcWing题库
问题描述:一棵树的每个节点的“高兴度”是1,选一个节点之后就不可以选他相邻的子节点,求怎么选才能使得高兴度最大。
#include
#include
#include
using namespace std;
const int N = 6010;
int n;
int happy[N]; //每个职工的高兴度
int f[N][2]; //上面有解释哦~
int e[N],ne[N],h[N],idx; //链表,用来模拟建一个树
bool has_father[N]; //判断当前节点是否有父节点
void add(int a,int b){ //把a插入树中
e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
void dfs(int u){ //开始求解题目
f[u][1] = happy[u]; //如果选当前节点u,就可以把f[u,1]先怼上他的高兴度
for(int i = h[u];~i;i = ne[i]){ //遍历树
int j = e[i];
dfs(j); //回溯
//状态转移部分,上面有详细讲解~
f[u][0] += max(f[j][1],f[j][0]);
f[u][1] += f[j][0];
}
}
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;i ++) scanf("%d",&happy[i]); //输入每个人的高兴度
memset(h,-1,sizeof h); //把h都赋值为-1
for(int i = 1;i < n;i ++){
int a,b; //对应题目中的L,K,表示b是a的上司
scanf("%d%d",&a,&b); //输入~
has_father[a] = true; //说明a他有爸爸(划掉)上司
add(b,a); //把a加入到b的后面
}
int root = 1; //用来找根节点
while(has_father[root]) root ++; //找根节点
dfs(root); //从根节点开始搜索
printf("%d\n",max(f[root][0],f[root][1])); //输出不选根节点与选根节点的最大值
return 0;
}
待强化知识点:
寻找状态转移方程(根据情况出现的不同情况进行计算)
用链表模拟建立树
dfs回溯之后的操作
P1223 排队接水(贪心)
问题描述:
代码:
#include
#include
#include
using namespace std;
double sum;
long int n;
long long int t[1001],a[1001];
double ans;
int main(int argc, const char * argv[])
{
cin>>n;
int x;
for(int i=1;i<=n;i++)
{
cin>>x;
a[i]=x;
t[i]=x*1001+i;
}
sort(t+1,t+1+n);
for(int j=1;j<=n;j++)
{
cout< 这个题需要用到计算相关的技巧。
学习:
1.给定一个数组(有这个数组的值的最大值范围比如<=1000), 给一个数组,输出从小到大排序的序号,只需要 t[i]=x*1001+i存入数据,之后取模t[j]%1001 ,就可以得到i(依次存入数据的顺序,即是数组的下标)
2.t[j]/1001,除过后的小数点后的余数的没有的,所以只要x*1001+i(i不大于1001)是不影响(x*1001+i)/1001 = x 的
教训:理解题目意思,求等待时间是不算自己打算的时间的。所以 sum += a[t[j]%1001]*(n-j);中的n-j十分的合理。如果意思是等待接水时间加自己接水时间的总和的平均值就是要n-j-1(或者n-j,j从0开始计数,n还是从10开始计数)