KMP算法:找出字符串中第一个匹配项的下标
题目描述
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad" 输出:0 解释:"sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto" 输出:-1 解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
思路
暴力匹配
我们可以让字符串 needle与字符串 haystack的所有长度为 m 的子串均匹配一次。我们每次匹配失败即立刻停止当前子串的匹配,对下一个子串继续匹配。如果当前子串匹配成功,我们返回当前子串的开始位置即可。如果所有子串都匹配失败,则返回 −1。很明显时间复杂度是O(m*n)。有没有更好的算法呢?这下就轮到我们的主角------KMP算法上场了。
KMP算法
要学会KMP算法,我们需要知道这些:
- 何为KMP算法
- KMP算法有什么用
- 什么是next数组
- 如何得到next数组
- 如何使用next数组来匹配
- 如何代码实现整个算法
何为KMP算法
说到KMP,先说一下KMP这个名字是怎么来的,为什么叫做KMP呢?因为是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP。
KMP算法有什么用
KMP主要应用在字符串匹配上。KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。所以如何记录已经匹配的文本内容,这就得靠next数组了。
什么是next数组
next数组其实就是一个前缀表(prefix table)。前缀表有什么作用呢?前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
那前缀表是是如何记录的呢?
首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
所以前缀表的具体含义:记录下标i之前(包括i)的字符串中,有多大长度(最大长度)的相同前缀后缀。
例如模式串 s = "aabaac" , 其对应的前缀表为 0,1,0,1,2,1。
如何得到next数组
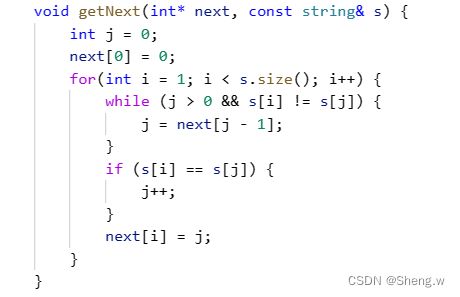
我先给出代码,直接根据代码讲解可能更清楚些。
其中 j 表示最长前缀的下一个下标,例如模式串 s = "aabaac" ,当 j 等于2时,表示此时最长前缀为"aa",所以 j 也可以理解成此时最长前缀的长度。
根据next数组的定义,我们可以直接得出next[0]的值为0,j 我们初始化为0。
在for循环里,i 表示我们当前遍历到的字符下标。每遍历一个字符,有两种情况,即s[i] == s[j]和
s[i] != s[j]。当二者不相等时,我们让 j 回溯到与s[j]==s[i]的下标处。因为我们可能要回退多次,所以我们必须使用循环连续回退。
有可能 j 回退到下标0处,s[i]依然不等于s[j],当然也有可能相等。如果相等,那我们的 j 便可以加1了。表示我们最大相同前后缀的长度增长了1.这就对于我们代码中的 if 分支。最后,我们就可以得到此时next[i] 处的值了,直接赋值就好啦。
如何使用next数组来匹配
假设我们的主串 haystack="aabaabaac",我们的模式串needle="aabaac"。
根据如何得到next数组这个流程,我们可以得到next数组为 0,1,0,1,2,1。
我们让两个指针分别指向两个字符串,假设 i 指向haystack,j 指向needle。
当haystack[i]==needle[j] 时,i 和 j 同时向后移动一位,此时判断 j 是否遍历完整个模式串。
当haystack[i] != needle[j] 时,我们就可以根据next数组让 j 回溯了。这里我们同样可能要回退多次,所以我们也必须使用循环连续回退。
由于我们的 i 是一直往后遍历的,所以KMP算法的时间复杂度为O(m+n),明显效率提高了很多。
如何代码实现整个算法
C++版本
Java版本