GDPU 数据结构 天码行空12

数据结构实验十二 图的遍历及应用

一、【实验目的】

1、 理解图的存储结构与基本操作；
2、熟悉图的深度度优先遍历和广度优先遍历算法
3、掌握图的单源最短路径算法

二、【实验内容】

1.根据下图邻接矩阵，编程实现该图的深度与广度优先遍历算法，输出遍历序列。

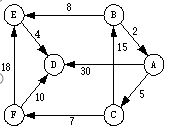
2.单源节点最短路径问题
问题描述:求从有向图的某一结点出发到其余各结点的最短路径。
基本要求:
（1）有向图采用邻接矩阵表示。
（2）单源节点最短路径问题采用Dijkstra算法。
（3）输出有向图中从源结点T到其余各结点的最短路径和最短路径值。

三、实验源代码

CPP

#include
#include
#include
#include
using namespace std;

const int N = 6;
const int M = N*N;
const int INF = 0x3f3f3f3f;
const int 无边 = -1;

int g[N][N]; //grap数组记录邻接矩阵【-1 表示不可达】
bool vs[N];//visted数组记录结点是否已经被访问过

void add(int a, int b, int c)
{
	// 邻接矩阵加边
	g[a][b] = c;
}

void init()
{
	for(int i = 0; i < N; i++)
		for(int j = 0; j < N; j++)
			g[i][j] = 无边;//初始化为不可达状态【-1】
	// A B C D E F
	// 0 1 2 3 4 5
	// 加边
	add(1, 0, 2);
	add(2, 1, 15);
	add(0, 2, 5);
	add(0, 3, 30);
	add(2, 5, 7);
	add(1, 4, 8);
	add(4, 3, 4);
	add(5, 3, 10);
	add(5, 4, 18);
}

void print()
{
	// 输出邻接矩阵
	cout << "输出邻接矩阵:" << endl;
	cout << "   A  B  C  D  E  F" << endl;
	char c = 'A';
	for (int i = 0; i < N; i++)
	{
		cout << c++ << "  ";
		for (int j = 0; j < N; j++)
			printf("%-2d ",g[i][j]);
//          cout << g[i][j] << " ";
		cout << endl;
	}
}

//深度优先遍历
// u 是当前访问的点
void dfs(int u)
{
	cout << char(u+'A') << " " ;
	vs[u] = true;//标记以访问
	for(int i = 0; i < N; i++)//访问当前结点可达的结点（有边）
	{
		int e = g[u][i];
		if(vs[i])//已访问过
			continue;
		if(e == 无边)//无边
			continue;
		dfs(i);		
	}
}

//广度优先遍历
// u 是当前访问的点
void bfs(int u)
{
	memset(vs,false,sizeof(vs));//初始化访问表为 未访问状态
	vs[u] = true;
	queue<int> q;//队列（先进先出）
	q.push(u);
	while(!q.empty()){
		int t = q.front();//取队头
		cout << char(t+'A') << " " ;
		q.pop();//队头出列
		for(int i = 0; i < N; i++)//访问当前结点可达的结点（有边）
		{
			int e = g[t][i];
			if(vs[i])//已访问过
				continue;
			if(e == 无边)//无边
				continue;
			q.push(i);
			vs[i] = true;
		}
	}
}



int dist[N];//距离数组
int pre[N];//pre[i] 记录最短路径上，点 i 的前一个结点
//输出路径
void printRoute(int x)
{
	cout << "\nA到" << char(x + 'A') << "的最短路径长度为： " << dist[x] << endl;
	cout << "最短路径途径节点：";
	vector<int> v;
	while(x != -1){
		v.push_back(x);
		x = pre[x];
	}
	for(int i = v.size()-1; i >= 0; i--)
		cout << char(v[i]+'A') << " " ;
	cout << endl;
}

//单源最短路 Dijkstra算法
void dijkstra(int u)//u表示起点
{
	cout << "\n\nDijkstra算法求最短路径"<<endl;
	memset(vs,false,sizeof(vs));//初始化访问表为 未访问状态
	memset(dist,0x3f,sizeof(dist));//初始化距离表为 无穷大
	memset(pre,-1,sizeof(pre));//初始化所有结点的前一个节点为 -1
	dist[u] = 0;
	for(int i = 0; i < N; i++)
	{
		int t = -1;
		for(int j = 0; j < N; j++)//找n次
		{
			if(!vs[j] && (t == -1 || dist[j] < dist[t]))//循环找当前最小距离的点
				t = j;
		}
		printRoute(t);
		vs[t] = true;
		for(int j = 0; j < N; j++)//用当前最小距离的点尝试去更新其他点的距离
		{
			if(g[t][j] == 无边)
				continue;
			if(dist[j] > dist[t] + g[t][j])
			{
				dist[j] = dist[t] + g[t][j];
				pre[j] = t;//记录前驱节点
			}
		}	
	}	
}
int main()
{
	init(); // 初始化图
	print(); // 输出邻接矩阵和邻接表
	cout<< "\n深度优先遍历：";
	memset(vs,false,sizeof(vs));//初始化访问表为 未访问状态
	dfs(0);
	cout<< "\n广度优先遍历：";
	bfs(0);
	dijkstra(0);
	return 0;
}

C

#include
#include
#include
#include

#define N 6
#define M (N * N)
#define INF 0x3f3f3f3f
#define NO_EDGE -1

int g[N][N]; // graph数组记录邻接矩阵【-1 表示不可达】
bool vs[N]; // visited数组记录结点是否已经被访问过

void add(int a, int b, int c)
{
    // 邻接矩阵加边
    g[a][b] = c;
}

void init()
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            g[i][j] = NO_EDGE; // 初始化为不可达状态【-1】
        }
    }
    // A B C D E F
    // 0 1 2 3 4 5
    // 加边
    add(1, 0, 2);
    add(2, 1, 15);
    add(0, 2, 5);
    add(0, 3, 30);
    add(2, 5, 7);
    add(1, 4, 8);
    add(4, 3, 4);
    add(5, 3, 10);
    add(5, 4, 18);
}

void print()
{
    // 输出邻接矩阵
    printf("输出邻接矩阵:\n");
    printf("   A  B  C  D  E  F\n");
    char c = 'A';
    for (int i = 0; i < N; i++)
    {
        printf("%c  ", c++);
        for (int j = 0; j < N; j++)
        {
            if (g[i][j] == NO_EDGE)
            {
                printf(" - ");
            }
            else
            {
                printf("%-2d ", g[i][j]);
            }
        }
        printf("\n");
    }
}

//深度优先遍历
// u 是当前访问的点
void dfs(int u)
{
    printf("%c ", u + 'A');
    vs[u] = true; // 标记已访问
    for (int i = 0; i < N; i++) // 访问当前结点可达的结点（有边）
    {
        int e = g[u][i];
        if (vs[i]) // 已访问过
            continue;
        if (e == NO_EDGE) // 无边
            continue;
        dfs(i);
    }
}

//广度优先遍历
// u 是当前访问的点
void bfs(int u)
{
    memset(vs, false, sizeof(vs)); // 初始化访问表为未访问状态
    vs[u] = true;
    printf("%c ", u + 'A');
    int queue[N];
    int front = 0, rear = 0;
    queue[rear++] = u;
    while (front != rear)
    {
        int t = queue[front++];
        for (int i = 0; i < N; i++) //访问当前结点可达的结点（有边）
        {
            int e = g[t][i];
            if (vs[i]) //已访问过
                continue;
            if (e == NO_EDGE) //无边
                continue;
            printf("%c ", i + 'A');
            queue[rear++] = i;
            vs[i] = true;
        }
    }
}

int dist[N];   //距离数组
int pre[N];    //pre[i] 记录最短路径上，点 i 的前一个结点

//输出路径
void printRoute(int x)
{
    printf("\nA到%c的最短路径长度为：%d\n", x + 'A', dist[x]);
    printf("最短路径途径节点：");
    int v[N], cnt = 0;
    while (x != -1)
    {
        v[cnt++] = x;
        x = pre[x];
    }
    for (int i = cnt - 1; i >= 0; i--)
    {
        printf("%c ", v[i] + 'A');
    }
    printf("\n");
}

//单源最短路 Dijkstra算法
void dijkstra(int u) //u表示起点
{
    printf("\n\nDijkstra算法求最短路径\n");
    memset(vs, false, sizeof(vs));   //初始化访问表为未访问状态
    memset(dist, INF, sizeof(dist)); //初始化距离表为无穷大
    memset(pre, -1, sizeof(pre));    //初始化所有结点的前一个节点为-1
    dist[u] = 0;
    for (int i = 0; i < N; i++)
    {
        int t = -1;
        for (int j = 0; j < N; j++) //找n次
        {
            if (!vs[j] && (t == -1 || dist[j] < dist[t])) //循环找当前最小距离的点
                t = j;
        }
        printRoute(t);
        vs[t] = true;
        for (int j = 0; j < N; j++) //用当前最小距离的点尝试去更新其他点的距离
        {
            if (g[t][j] == NO_EDGE)
                continue;
            if (dist[j] > dist[t] + g[t][j])
            {
                dist[j] = dist[t] + g[t][j];
                pre[j] = t; //记录前驱节点
            }
        }
    }
}

int main()
{
    init();  // 初始化图
    print(); // 输出邻接矩阵和邻接表
    printf("\n深度优先遍历：");
    memset(vs, false, sizeof(vs)); //初始化访问表为未访问状态
    dfs(0);
    printf("\n广度优先遍历：");
    bfs(0);
    dijkstra(0);
    return 0;
}