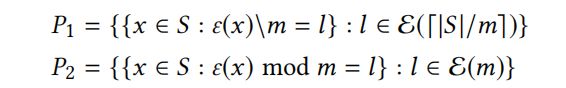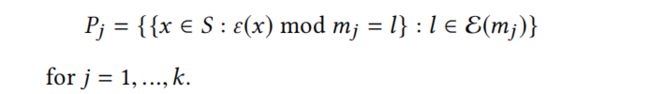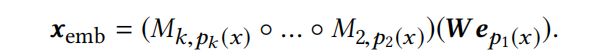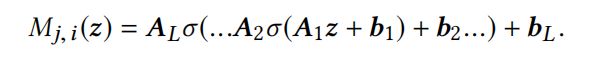Embedding压缩之hash embedding

在之前的两篇文章 CTR特征重要性建模：FiBiNet&FiBiNet++模型、CTR特征建模：ContextNet & MaskNet中，阐述了特征建模的重要性，并且介绍了一些微博在特征建模方面的研究实践，再次以下面这张图引出今天的主题：

在推荐系统中，特征Embedding是极其重要的一部分，并且占了模型体积的大头，消耗巨大的显存，因此如果可以对特征Embedding进行压缩，那么是可以节省许多计算资源的。

因此，这篇文章的主题便是Embedding压缩，而embedding hash便是一种实用的手段。

feature embedding

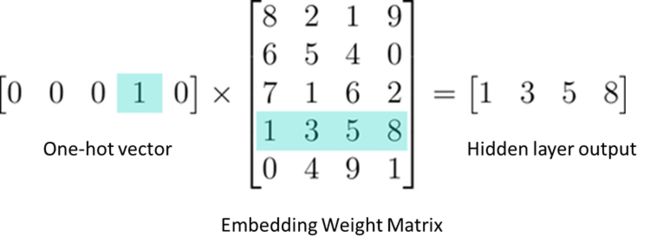
在embedding技术推广之前，离散特征更多是用one-hot进行编码的。比如“学历”这个特征域(field)，假如存在5种特征值：初中及以下、高中、本科、硕士、博士，那么“硕士”就是第4种特征值，那么one-hot编码之后就为“[0,0,0,1,0]”，如下图-左，同理“本科”即为"[0,0,1,0,0]"。

one-hot的缺点就是在于如ID类特征，其维度非常高，并且导致数据十分稀疏。

那么引入Embedding后，就需要一个Embedding矩阵 $W^{N\times d}$，如下图-中，将其映射到稠密的向量如下图-右，N为特征域的特征值unique数，比如上面的学历N=5，d为Embedding的维度，即映射后的向量维度，下图即d=4：

$x_{emb}=W^T{e}_i,e_i\in {\mathbb{R}}^N,e_i$ is ont-hot vector

所以，在实际特征工程中，往往会把特征转化为唯一的ID: unique id，去Embedding矩阵中寻找unique id对应索引的特征向量。如上述的“硕士”即unique id=4（从1开始，但实际是由0开始），对应则是第4行的特征向量，本科即为unique id=3，为第3行的特征向量：

$x_{emb}=W_{i,:},i=uniqueid$

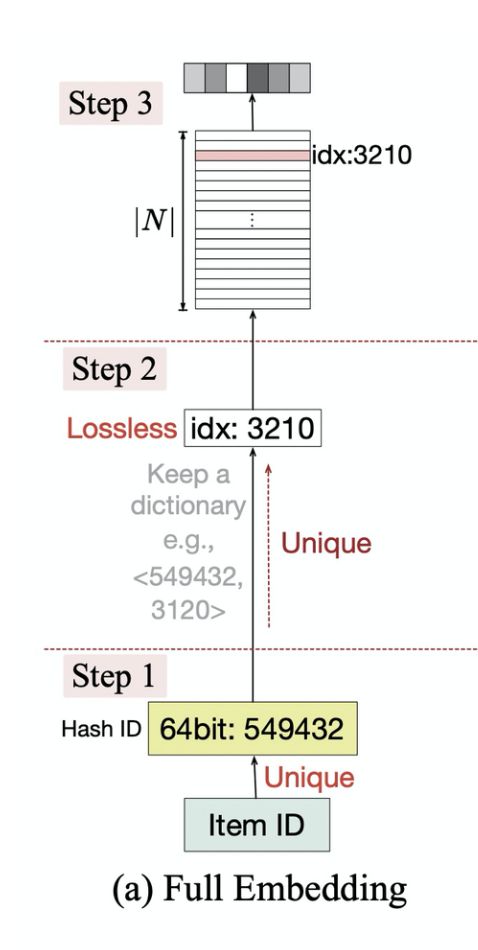
对应的特征embedding映射步骤如下图：

ID类的特征表示学习会为每一个特征值学习一个特征向量，Embedding矩阵W的存储开销是随着N线性增长的。而真实场景下的推荐系统中，特征值是非常多的，如user id和item id，并且还有一些id交叉，N很容易达到几百万甚至上亿，会导致Embedding矩阵W非常大。

hash embedding

论文：Feature Hashing for Large Scale Multitask Learning

链接：https://arxiv.org/pdf/0902.2206.pdf

定义一个散列函数hash function：

$\mathcal{T}\to B=\{1,2,...,M\},|\mathcal{T}|=N$

表示从特征空间为N的$\mathcal{T}$中取任意一个特征值，可以转化为小于等于M的hash id：最常见的hash function便是取模（模数为M），将原来的特征值进行hash编码得到hash code，然后对M取模后的余数作为hash id。

再定义一个Embedding矩阵$W^{M\times d}$，那么根据hash id，可以在$W^{M\times d}$找到对应索引的向量，而不需要去原来的$W^{N\times d}$。

这样原本的Embedding矩阵 $W^{N\times d}$就可以用$W^{M\times d}$来代替，因为$N\gg M$，大大减少了Embedding矩阵的参数量。

而这种做法显然存在很大的缺点：不同的特征值可能会映射到相同的索引值，即出现hash冲突(collision)的情况，导致对应相同的embedding向量，使得模型无法区分这些特征，损失模型效果。

hash vs. full embedding

full embedding是从Embedding矩阵 $W^{N\times d}$将每个特征值映射到唯一独有的embedding，而hash embedding则是通过hash function将N降低到M，即$W^{M\times d}$。

但其实full embedding也是hash embedding的一种特殊形式，即当$M\ge N$时。因此这可以引伸到另外一个概念：词表(dictionary)。

• full embedding需要将每种特征值提前一一映射对应的unique id，这也可以理解为一种特殊的hash编码。但是这相当于需要创建词表，类比NLP任务，每个词需要提前映射到唯一ID；
• 而hash embedding则可以通过hash随机编码+取模的方法将所有特征值映射到$\{1,2,...,N\}$，无需提前创建词表；
• 因此hash embedding可以用来代替full embedding，并且适合提前创建词表比较困难，或者词表动态变化的场景，但不完全等效，因为可能存在hash冲突(collision)。

multi-hash

论文：Hash Embeddings for Efficient Word Representations

链接：https://arxiv.org/abs/1709.03933

这篇论文的应用场景是在NLP任务中为每个word学习向量represention，并引入hash embedding的改进，但推荐系统的特征embedding是可以类比借鉴的。但是为了全文的表达统一，还是以特征embedding的角度进行阐述，而非word embedding。

为了解决单hash的不同特征值id冲突(collide)的问题，论文提出了使用k个hash functions，然后再用k个可训练参数，为每个特征值选择最合适(best)的hash function，实际中更好的方法则是将多个hash function组合起来得到最终的hash embedding。

除了能够压缩模型参数量以外，hash embedding还存在以下优点：

• 如上所述，无需提前创建词表，并且支持动态扩展词表。不过这同样存在缺点：线上推理时，对于未知(新)特征值，仍能得到对应的hash embedding，但其实更好的做法是将未知特征值置为一个默认统一的(填充)特征值；
• 可以通过训练来解决hash冲突问题：单个hash function容易出现冲突，但多个hash functions全部冲突的可能性相对很低，因此对于每个特征值，通过importance parameters组合所有hash component vectors为每个特征值学习一个有效并且接近独有的向量表征；
• hash embedding可以理解为一种能够修剪隐式词表的机制(implicit vocabulary pruning)，不重要的词的import parameters会接近0；它也类似于product quantization技术。

（double hash是k=2的情况，概念仍然是multi-hash）

##hash步骤

multi-hash生成hash embedding的具体步骤如下：

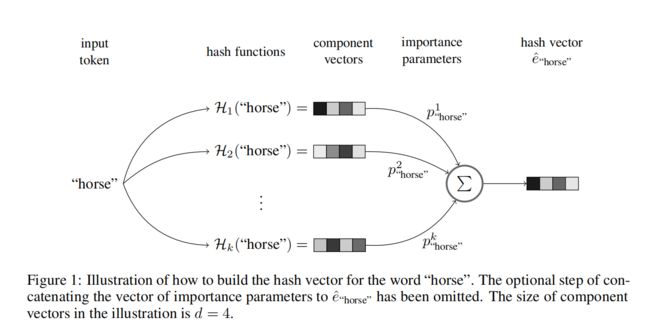
1. 定义k个不同的hash functions ${\mathcal{H}}_1,...,{\mathcal{H}}_k$ 来选择k个向量，如上图[multi-hash过程]的component vector，从一个共享的Embedding矩阵中；
2. 为component vector分配可学习的权重参数，称为import parameters，然后进行相加，如下式：${\hat{e}}_w={\sum }_{i=1}^k{p}_w^i{\mathcal{H}}_i(w).p_w=(p_w^1,...,p_2^k)\in {\mathbb{R}}^k$，可以理解为学习每个hash function的component vector的重要性。每个特征值的hash embedding的import parameters是独有不共享的。
3. (可选)将向量的权重参数$p_w$拼接到${\hat{e}}_w$，得到最后的hash向量$e_w$

${\mathcal{H}}_i(w)=E_{D_2(D_1(w))}$表示将特征值w如何结合hash function得到对应的向量，与上述一致，不再赘述：

参数量从原来的$K\times d$变为$K\times k+B\times d$，K为特征值的unique数量，k为hash function的数量，B为component vectors数量即hash function的映射范围(比如取模的模数)，d为embedding的维度。大部分场景下k取5以内，而$K>10\cdot B$，因此参数量是可以显著减少的。

hybrid hash

论文：Model Size Reduction Using Frequency Based Double Hashing for Recommender Systems

链接：https://arxiv.org/abs/2007.14523

这篇论文是推特在2020年发表的，提出了一种混合hash技术(hybrid hash)，结合了特征频次的double hash(即上述mult-hash)，论文的主要贡献为下面三个点：

1. 直击深度学习推荐系统的模型体积问题，提出了混合hash技术(hybrid hash)，大大减少了Embedding layers的内存容量；
2. 所有的特征不是同等重要的。double hash对所有特征是相同对待处理的，而推特则是引入特征频次统计，让更为重要的特征避免hash冲突；
3. 两次hash codes的计算其实也是昂贵的，特别是在几百万特征的场景。而混合hash仅需要对频次较低的特征进行double hash。

Double hashing

与上述的multi-hash基本一致，这里的hash functions的数量取2，因此叫double hashing。

定义两个hash function $h_1,h_2$：$\mathcal{T}\to \{1,2,...,B\}$，直接将离散的特征值映射为两个hash codes $h_1(f),h_2(f)$。

不过推特并没有引入import parameters，而是**使用元素位相加(element wise summation)或者拼接(concatenation)**的方式来组合两个hash vectors：$g(E(h_1(f)),E(h_2(f)))$。

频次 hashing

某些特征在推荐模型中是更为重要的，如果这些特征值发生了冲突，容易导致我们并不想见到的后果。因此，论文对不同重要性的特征值进行不同的处理，这里引入特征值的频次作为特征的重要性指标，其思想也是比较简单直接，如下图所示：

• 让频次top-K的特征值映射到唯一的ID，即上述提到的unique id：$\{0,...,k-1\}$，这样这些特征值就能够映射到唯一独有的向量，避免了hash冲突；
• 而对于剩下低频的特征值，则是使用double hashing来聚合得到hash embedding；
• 使用hybrid hash的方法，既能避免重要特征值因为embedding共享带来的负面影响；又能大大减少两次hash codes计算的次数，因为仅低频特征值才需要，对线上服务的性能提升很大。

QR Trick

论文：Compositional Embeddings Using Complementary Partitions for Memory-Efficient Recommendation Systems

链接：https://arxiv.org/abs/1909.02107

这篇论文是Facebook在2020发表的，其中的QR技巧（Quotient-Remainder Trick），提出互补分区的概念，既能保留hash embedding显著减少embedding容量的优点，又能保证最终产出unique embedding vector，即不存在冲突。

算法步骤

引入两个关键的操作：**取模（remainder）和取商（quotient/integer division）**来作为hash functions，整个实现步骤也比较简单：

1. 创建两个Embedding矩阵$W_1,W_2$
2. 计算x的unique id。论文的例子，离散变量x的集合 S = {dog, cat, mouse}，那么S的所有可能枚举为：$\epsilon (dog)=0,\epsilon (cat)=1,\epsilon (mouse)=2$
3. unique id取模之后映射到$W_1$得到第一个hash embedding，模数为m
4. unique id取商(即除以m留整数)之后映射到$W_2$得到第二个hash embedding
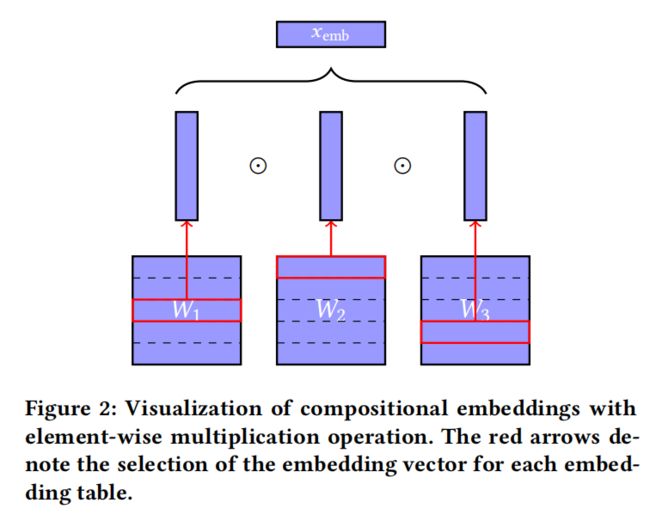
5. 最后两个hash embedding进行点积 $\odot$ (element-wise multiplication)作为最后的表征embedding

互补分区

定义1：给定集合S的分区$P_1,P_2,...,P_k$。对于所有的a和b，当$a\ne b$时，都存在一个分区i使得$[a{]}_{P_i}\ne [b{]}_{P_i}$，那么这些分区就是互补分区（Complementary Partition）。

比如，对于集合$S=\{0,1,2,3,4\}$，存在以下三种互补分区：

对于每个分区，也叫做bucket，其实就对应一个embedding table，里面的每一个元素会映射到一个embedding vector。

从上述的定义可以看出，互补分区是实现unique embedding vector的一种手段，因为总是存在一个bucket使得hash id不冲突。而恰好取模和取商结合正好是一种互补分区，称为商余互补分区（Quotient-Remainder Complementary Partitions）：记集合$\epsilon (n)=\{0,1,...,n-1\}$，即集合的元素 $n\in \mathbb{N}$。

给定一个 $m\in \mathbb{N}$

上式分别为对x进行取模和取商的两个集合分区，这便对应Quotient-Remainder Trick。

商余互补证明

为什么仅仅靠简单的两个hash操作：取模（remainder）和取商（quotient/integer division）就能得到unique embedding vector？这个问题可以转换为：为什么商余分区是互补的？

1. 第一种情况，当$[x{]}_{P_1}\ne [y{]}_{P_1}$或者$[x{]}_{P_2}\ne [y{]}_{P_2}$，无需证明
2. 第二种情况，当$[x{]}_{P_1}=[y{]}_{P_1}=l$，那么需要证明存在$[x{]}_{P_2}\ne [y{]}_{P_2}$：$\epsilon (x)=ml+r_{x}and\epsilon (y)=ml+r_x$，因为$x\ne y$，那么$\epsilon (x)\ne \epsilon (y)$，因此$r_x\ne r_y$。又因为 $\epsilon (x)modm=r_x$，并且$\epsilon (y)modm=r_y$，得证 $[x{]}_{P_2}\ne [y{]}_{P_2}$
3. 第三种情况，当$[x{]}_{P_2}=[y{]}_{P_2}$，那么需要证明存在$[x{]}_{P_1}\ne [y{]}_{P_1}$：$\epsilon (x)=m{l}_x+rand\epsilon (y)=m{l}_y+r$，因为$x\ne y$，那么$\epsilon (x)\ne \epsilon (y)$，因此$l_x\ne l_y$。又因为，$\epsilon (x)\backslash m=l_x$，并且$\epsilon (y)\backslash m=l_y$，得证 $[x{]}_{P_1}\ne [y{]}_{P_1}$
4. 到此证明完毕。其实大白话来讲就是，商余这两个操作下，不相同的x和y，不可能商数和余数都相等。

其他互补分区

记集合$\epsilon (n)=\{0,1,...,n-1\}$，即集合的元素 $n\in \mathbb{N}$

（1）纯互补分区（Naive Complementary Partition）：$P=\{\{x\}:x\in S\}$

这样的P也属于互补分区的定义范围，其实就是集合里面的每个元素作为单独的一个分区，相当于full embedding table ($|S|\times D$)

（2）商余互补分区（Quotient-Remainder Complementary Partitions），如上述。

（3）泛化的商余互补分区（Generalized Quotient-Remainder Complementary Partitions）：给定 $m_i\in \mathbb{N},i=\{1,...,k\}$，并且$|S|\le {\prod }_{i=1}^k{m}_i$

其中，$M_i={\prod }_{i=1}^{j-1}{m}_{i}forj=2,...,k$。这是一种更为泛化的商余互补分区形式。

（4）Chinese Remainder Partitions：给定一批互质的 $m_i\in \mathbb{N},i=\{1,...,k\}$，即对于所有的$i\ne j，gcd(m_i,m_j)=1$。并且$|S|\le {\prod }_{i=1}^k{m}_i$，那么下式这些分区也是互补分区：

其中，$gcd(m_i,m_j)$表示$m_i,m_j$的最大公约数为1。

泛化的商余分区和Chinese Remainder Partitions的互补分区证明，有兴趣的可以去看看论文。

组合方式

多个分区得到的embedding vectors进行一些组合操作来作为最终的特征embedding表征，这与其他hash方法一样。论文提到的embeddings组合方式其实同样可以应用到上面别的hash方法，当然也可以应用到其他模型中的embedding组合。

常规的组合方式如以下三种：

• 拼接（Concatenation）：$w(z_1,...,z_k)=[z_1^T,...,z_k^T{]}^T$
• 相加（Addition）：$w(z_1,...,z_k)=z_1+...+z_k$
• 点击/元素位相乘（Element-wise Multiplication）：$w(z_1,...,z_k)=z_1\odot ...\odot z_k$

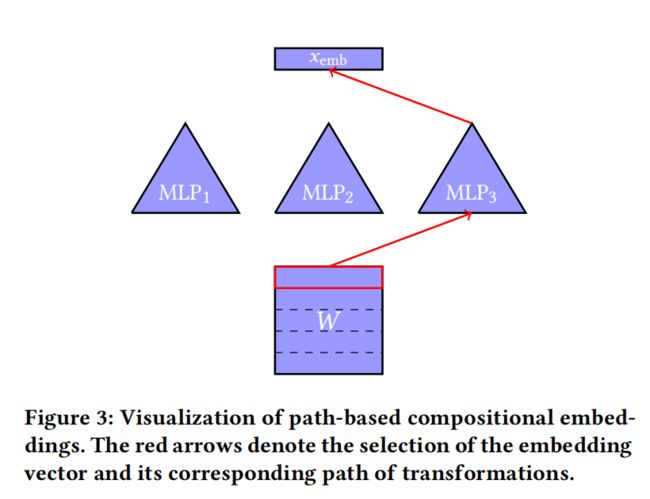
基于路径的组合

从第一个分区开始，为每个分区定义一系列不同的变换(transformations)集合，称为path-based compositional embeddings，像path一样，一个分区一个分区传递下去。具体的表达如下：

给定一系列互补分区 $P_1,P_2,...,P_k$，为第一个分区定义embedding table $W\in {\mathbb{R}}^{|P_1|\times D_1}$，

接着为每个分区定义一系列函数$，M_j=\{M_{j,i}:{\mathbb{R}}^{D_{j-1}}\to {\mathbb{R}}^{D_j}:i\in \{1,...,|P_i|\}\}$

那么$x\in S$的组合embedding，则通过下式的转换得到：

其中，$p_j:S\to \{1,...,|P_j|\}$ 是将x映射到对应embedding table的索引的函数。

更具体一点，函数$M_{j,i}$包括以下两个部分：

1. 线性函数：$M_{j,i}(z)=Az+b$，参数为$A\in {\mathbb{R}}^{D_j\times D_{j-1}}$和$b\in {\mathbb{R}}^{D_j}$

2. MLP（Multilayer perception）：

   其中，L为layers的层数，$\sigma :\mathbb{R}\to \mathbb{R}$是激活函数，如ReLU或者sigmoid。

   $A_1\in {\mathbb{R}}^{d_1\times d_0}，A_2\in {\mathbb{R}}^{d_2\times d_1}，...，A_L\in {\mathbb{R}}^{d_L\times d_{L-1}}$

   $b_1\in {\mathbb{R}}^{d_1}，b_2\in {\mathbb{R}}^{d_2}，...，b_L\in {\mathbb{R}}^{d_L}$

   $d_0=D_{j-1}，d_L=D_j，D_j\in \mathbb{N}forj=1,...,k-1$

直白地讲，就是多层DNN一样即MLP，从第一个分区开始，一层接着一层，最后一层输出的便是最终的组合embedding。

总结

hash embedding是压缩embedding矩阵参数量的一种有效手段，原理其实很简单，本文也讲得有些啰嗦了，最后再总结下几种hash：

• 单hash：直接长度为N的unique id集合映射到长度为M的hash id集合，$N\gg M$，例如简单的取模函数，但可能存在hash冲突，导致不同的特征值映射到相同的embedding，影响模型效果；
• 多hash：使用多个hash functions来降低冲突的概率，并且还引入可学习的import parameters，每个特征值独立学习每个hash embedding的重要性权重。
• 混合hash：推特引入频次作为特征值的重要性指标，重要(频次top-K)的特征值使用full embedding，而剩余的特征值则使用double hashing即两个hash functions，即可以提升模型效果，又能大大减少hash计算的次数，提升服务性能；
• QR Trick：Facebook仅仅使用取模（remainder）和取商（quotient/integer division）两个hash functions，就可以解决hash冲突的问题；
• 组合embedding：包括常规的拼接、相加和点积，Facebook还提出了基于路径的组合方式。

代码实现

QR Trick实现：github